2. Оптимізація нелінійної функції однієї перемінної

Існують дві причини вивчення методів оптимізації функції однієї перемінної. Перша з них полягає в тому, що на одномірних задачах можна демонструвати багато труднощів, з якими приходиться зіштовхуватися при рішенні нелінійних оптимізаційних задач. Немає необхідності для роз’яснення цих труднощів звертатися до багатомірних задач, іноді ще менш зрозумілим. Друга причина полягає у тому, що в багатьох методах рішення нелінійних оптимізаційних задач з багатьма перемінними на тому або іншому кроці, власне кажучи, використовуються алгоритми оптимізації для однієї перемінної. Отже, для застосування методів, призначених для рішення оптимізаційних задач загального виду, потрібне знайомство з методами оптимізації одномірних моделей.

Почнемо з того, що в рамках усього наступного обговорення обмежимося розглядом „максимізації” у сенсі оптимізації. [Якщо в реальній задачі потрібно мінімізувати цільову функцію , то можна переформулювати модель, максимізуючи ].

Спочатку розглянемо задачу максимізації лінійної функції однієї перемінної . Відповідь тут настільки тривіальна, що вона навіть не обговорювався в розділах, присвячених лінійному програмуванню, однак у даному розділі вона використовується як відправна точка для розгляду оптимізаційних методів у нелінійних ситуаціях. Якщо на х не накладається ніяких обмежень, то при будь-якому значення цільової функції може бути зроблене як завгодно великим. Якщо ж х може приймати тільки обмежені значення, тобто , то оптимально при , а – при .

О

Приклад 2

тже, оптимальним завжди є рішення, що відповідає екстремальній точці. Однак, якщо ми відмовимося від допущення про лінійність функції , стають можливими також інші ситуації; деякі з них відображені на рис. 7.1.

Приклад 1 Приклад 3 Приклад 4 Приклад 5 Приклад 6

Рис. 7.1. Нелінійні функції

Функція може необмежено зростати, навіть якщо значення х обмежені; функція , обмежена зверху, не обов’язково досягає максимуму, причому поза залежністю від того, чи обмежені значення х. При будь-якому вичерпному розгляді алгоритмічних підходів до максимізації нелінійної функції однієї перемінної необхідно враховувати всі ці різні можливості. Однак відповідно до цілей цього розділу зручно припустити, що:

I) х лежить у межах кінцевого сегмента , тобто , де ;

II) функція безперервна та обмежена зверху для всіх х на сегменті І.

Важливим наслідком цих двох допущень є те, що досягає максимуму при значенні х, що знаходиться на сегменті І.

Послідовний пошук. Розглянемо функцію , графік якої зображений на рис. 7.2. Максимальне значення досягається при х = 1. Як неважко уявити, для функцій такого типу адаптивний процес пошуку максимуму навряд чи виявиться ефективним: він може привести до гарних результатів лише випадково. Для ілюстрації припустимо, що перше значення х, що перевіряється, менше а. Тоді можливо, що кожне наступне значення х буде все більше і більше наближатися до а, але не буде перевищувати а, оскільки є локальний максимум. Далі, припустимо, що перше значення х, що перевіряється, знаходиться на сегменті [d, е]. Тоді, очевидно, послідовний пошук закінчиться відразу ж, оскільки як при невеликому збільшенні, так і при невеликому зменшенні значення х функція не змінює своєї величини та її поліпшення не уявляється можливим. Адаптивні методи, що викладаються нижче, не можуть гарантувати, що, насамкінець, область пошуку звузиться до невеликого інтервалу навколо f (рис. 7.2).

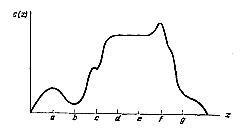
Рис. 7.2. Приклад функції, що володіє багатьма локальними оптимумами

Однак розгляд функції на сегменті [0, g], власне кажучи, є більш загальною ситуацією, ніж це дійсно необхідно для досягнення безпосередньо поставленої мети, а саме розробки адаптивних методів пошуку оптимуму функцій одної перемінної, котрі надалі будуть використані при рішенні багатомірних нелінійних задач оптимізації.

З цієї причини і вводиться додатковий постулат щодо форми функції . Зокрема, розглянемо так називану унімодальну функцію, що володіє наступними властивостями: якщо х є єдине оптимальне значення х на сегменті І, то зі зростанням х строго зростає при і строго убуває при . Якщо максимальне значення на І, що позначимо , має місце не для однієї точки, а для деякого інтервалу оптимальних значень х, то строго зростає до досягнення , зберігає це значення уздовж всього інтервалу оптимальних х, а потім строго убуває. Формальне і більш точне визначення такої функції має такий вигляд: функція є унімодальною на сегменті І, якщо для будь-яких та на І, де та , функція задовольняє умовам

при ,

(унімодальна) (7.6)

при ,

Функція є унімодальною, якщо вона увігнута, тобто, якщо для будь-яких та на І, де , і для будь-якого р, 0 ≤ р ≤ 1, функція задовольняє умові

(увігнута). (7.7)

Якщо функція має регулярну другу похідну , то еквівалентною умовою увігнутості є для всіх х. Якщо для всіх х, то строго увігнута. Тут і далі додатково до (I) і (II) вводиться умова:

унімодальна по х на сегменті І. (III)

Неважко перевірити, що введення умови (III) виключає можливість використання як сегмент I таких сегментів (рис. 7.2), як [b, g], однак умові (III) відповідають сегменти [b, е] та [е, g].

Тепер покажемо, яким чином введення умови (III) дозволяє застосувати адаптивний метод пошуку для знаходження інтервалу заданої величини, що містить те значення х, при якому досягається максимум .

Нехай відомо, що оптимальне значення х знаходиться на сегменті [A₁, А₂] і обчислені значення у двох точках х_лів та х_пр цього сегмента, причому х_лів < х_пр (перша точка розташована „лівіше”, а друга – „правіше”). Якщо , то не може зростати при , тому оптимальне повинно знаходитися на сегменті . Накресліть графік і поясніть, чому. У будь-якому випадку порівняння та дозволило скоротити довжину сегмента, на якому, як нам відомо, має знаходитися оптимальне значення х. Як неважко собі представити, є безліч різних алгоритмів послідовного пошуку, котрі можна розробити з урахуванням цієї властивості унімодальної функції.

Описуваний нижче метод, іноді іменований методом золотого перетину, має такі достоїнства, як простота та досить висока ефективність. Введемо позначення:

(7.7)

Значення цієї константи стане ясним після того, як буде викладений алгоритм пошуку максимального значення функції , де х знаходиться на сегменті І = [а₁, а₂].

Крок 1. Приймемо А₁ = а₁, А₂ = а₂, Н = А₁ – А₂, та .

Крок 2. Порівняємо та . У залежності від результатів порівняння перейдемо до кроку 3 або до кроку 4.

Крок 3. Якщо , приймемо та . Припинимо розрахунки, якщо Н досить мале. У супротивному випадку в якості нового х_пр виберемо попереднє х_лів, а в якості новий х_лів – точку ( ). Повернемося до виконання кроку 2.

Крок 4. Якщо , приймемо та . Припинимо розрахунки, якщо Н досить мале. У супротивному випадку в якості нового х_лів виберемо попереднє х_пр, а в якості нового х_пр – точку ( ). Повернемося до виконання кроку 2.

При заданому в (7.7) значенні r алгоритм має три важливі властивості. По-перше, після кожної ітерації нове значення Н в 1/r раз менше попереднього значення Н. Отже, після п ітерацій оптимальне значення х знаходиться на відомому сегменті, довжина якого дорівнює . Таблиця значень rⁿ для п ≤ 10 приведена на рис. 7.3.

n	rn	(0,5)n+1
1	0,6180	0,25
2	0,3820	0,125
3	0,2361	0,0625
4	0,1459	0,0313
5	0,0902	0,0156
6	0,0557	0,0078
7	0,0344	0,0039
8	0,0213	0,0020
9	0,0132	0,0010
10	0,0081	0,0005

Рис. 7.3. Показники скорочення довжини сегменту при

використанні методів золотого перетину та дихотомії

По-друге, після кожної ітерації х_лів та х_пр знаходяться на однаковій відстані від найближчих до них кінців сегменту, тобто .

По-третє, при виконанні кроку 2 (на всіх ітераціях, крім першої) новою є тільки одна з точок х_лів та х_пр, тому необхідно додатково обчислити тільки одне значення .

Інший метод адаптивного пошуку, іменований методом дихотомії або методом розподілу навпіл, можна побудувати таким чином, що у випадку його застосування буде використовуватися інформація про значення похідної функції для відмінних від оптимуму значень х. При даному методі враховується та обставина, що похідна унімодальної функції не змінює знака більше ніж один раз. Нехай не є звичайною монотонно зростаючою функцією. Це значить, що при х = a_t похідна є ненегативною при збільшенні х і залишається ненегативною доти, поки не досягне максимального значення; потім, при подальшому збільшенні х, похідна непозитивна. Отже, у точці з оптимальним значенням х похідна змінює знак; при розглянутому підході повторно звужується сегмент, на якому відбувається зміна знака. (Метод придатний і для монотонних функцій.)

Для застосування зазначеного методу необхідно вивести формулу похідної dc/dx і додатково припустити, що форма така, що dc/dx не тільки регулярна, але і дорівнює нулю тільки при оптимальному значенні х. (Неважко побудувати унімодальні функції на кінцевому сегменті І, що не задовольняють зробленим допущенням про вид функції. Такими функціями будуть, наприклад, кусочно-лінійні функції при неоптимальних значеннях х та функції, що мають або точку перегину, або точку з нескінченним значенням dc/dx). На кожній ітерації при використанні методу дихотомії довжина сегмента, на якому знаходиться оптимальне значення , скорочується у два рази. Після п вирахувань значення похідній dc/dx довжина сегмента складає 0,5ⁿ⁺¹(a₂ – а₁), тоді як після п розрахунків значення метод золотого перетину дозволяє скоротити сегмент тільки у rⁿ(a₂ – а₁) разів. Таким чином, коефіцієнт 0,5ⁿ⁺¹ варто порівнювати з коефіцієнтом rⁿ, значення якого приведені на рис. 7.3. Разом з тим, у випадку використання методу дихотомії можливі значні обчислювальні труднощі, якщо похідна dc/dx виявиться більш складним вираженням, ніж , наприклад коли .

Ідея алгоритму полягає в тім, що якщо для деякого спробного х_прб dc/dx > 0, то існує оптимальне значення таке, що . Аналогічно цьому якщо dc/dx < 0, те оптимальне значення . Опишемо пропонований алгоритм.

Крок 1. Нехай а₁ = а₁, а₂ = а₂ та Н = а₂ – а₁.

Крок 2. Приймемо . Обчислимо значення dc/dx у точці . Припинимо розрахунки, якщо dc/dx = 0, оскільки в цьому випадку є точкою оптимуму. У супротивному випадку в залежності від знака похідної перейдемо до кроку 3 або до кроку 4.

Крок 3. При dc/dx < 0 приймемо та . Припинимо розрахунки, якщо Н досить мале. У супротивному випадку повернемося до виконання кроку 2.

Крок 4. При dc/dx > 0 приймемо та . Припинимо розрахунки, якщо Н досить мале. У противному випадку повернемося до кроку 2.