Диэлектрики в электрическом поле

1. Электрический момент диполя (электрический дипольный момент).

2. Определение вектора поляризованности.

3. Эмпирическая связь вектора поляризованности с напряженностью электростатического поля.

4. Связь диэлектрической восприимчивости и относительной диэлектрической проницаемости вещества.

5. Связь поляризованности и поверхностной плотности связанных зарядов.

6. Напряженность поля в диэлектрике, выраженная как суперпозиция полей сторонних и связанных зарядов.

7. Определение вектора электрического смещения.

8. Связь векторов электрического смещения, поляризованности и напряженности электрического поля.

9. Теорема Гаусса для вектора электрического смещения (теорема Гаусса для электростатического поля в диэлектрике).

10. Электрическая емкость уединенного проводника или конденсатора.

11. Электрическая емкость уединенной проводящей сферы радиуса R, находящейся в бесконечной среде с диэлектрической проницаемостью.

12. Электрическая емкость плоского конденсатора.

13. Электрическая емкость батареи из N последовательно соединенных конденсаторов.

14. Электрическая емкость батареи из N параллельно соединенных конденсаторов.

15. Энергия электрического поля зараженного конденсатора.

16. Энергия электрического поля заряженного до потенциала проводника.

17. Объемная плотность энергии электрического поля.

18. Энергия электрического поля, сосредоточенная в некотором объеме V.

Энергетические характеристики

электростатического поля

Пример 1. По тонкой нити, изогнутой по дуге окружности, равномерно распределен заряд с линейной плотностью = 10 нКл/м. Определить потенциал  электрического поля, создаваемого таким распределенным зарядом в точке, совпадающей с центром кривизны дуги. Длина нити составляет 1/3 длины окружности и равна 15 см.

Решение. Для нахождения потенциала воспользуемся принципом суперпозиции для непрерывно распределенных вдоль линии зарядов. Выделим на нити элемент длины dl, на котором находится заряд dq = ·dl, который можно считать точечным. Потенциал поля, создаваемого этим зарядом в точке 0:

.

Согласно принципу суперпозиции, потенциал, создаваемый в точке 0 заряженной нитью, равен

.

Поскольку l = 2R/3, то _

Произведем вычисления и получим  В.

Пример 2. На тонком стержне длиной l равномерно распределен заряд с линейной плотностью нКл/м. Найти потенциал, созданный распределенным зарядом в точке А, расположенной на оси стержня и удаленной от его ближайшего конца на расстояние l.

Решение. Выделим на стержне малый участок длиной dх, на котором расположен заряд dq = ·dx, который можно рассматривать как точечный. Потенциал d, создаваемый точечным зарядом в точке А, равен

.

l l

dq

X A

dx

x

 Рис.2.10.

Согласно принципу суперпозиции, потенциал электрического поля, создаваемого в точке А заряженным стержнем равен:

.

Подставив числовые значения в системе СИ и произведя вычисления, получим 

Пример 3. Электрическое поле создано тонким стержнем, несущим равномерно распределенный по длине с линейной плотностью = 0,1 мкКл/м, заряд. Определить потенциал  поля в точке, удаленной от концов стержня на расстояние, равное длине стержня.

Решение. Выделим на стержне элементарный отрезок длиной dx, на котором распределен заряд dq = ·dx, который можно рассматривать как точечный. Потенциал поля, создаваемого этим зарядом в точке А, равноудаленной от концов стержня, равен

,

где r - расстояние от элементарного заряда dq до точки поля А, в которой определяем потенциал (рис.3).

A 

d

l

rd

_{}_

r

dx l

Рис.2.11.

Из рисунка следует, что dx = rd/cos. Подставив это выражение в формулу для d, получим

.

Интегрируя полученное выражение в пределах от ₁ до ₂ , получим потенциал, создаваемый всем зарядом, распределенным вдоль стержня:

.

В силу симметрии расположения точки А относительно концов стержня имеем _ = ₂ и поэтому

.

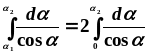Так как

,

то

 .

Подставляя пределы интегрирования, получим

.

Выполнив вычисления по этой формуле, найдем  = 990 B.

Пример 4. Электрическое поле создано длинным цилиндром радиуса R = 1 см, равномерно заряженным с линейной плотностью  = 20 нКл/м. Определить разность потенциалов двух точек этого поля, находящихся на расстоянии a₁ = 2 cм и a₂ = 2 cм от поверхности цилиндра в средней его части.

Решение. Для определения разности потенциалов воспользуемся интегральной связью между разностью потенциалов и напряженностью электрического поля:

. (1)

Так как цилиндр длинный и точки взяты вблизи его средней части, то для выражения напряженности поля можно воспользоваться формулой напряженности поля, создаваемого бесконечно длинным цилиндром:

.

Подставив это выражение в равенство (1), получим:

. (2)

Так как величины r₁ и r₂ входят в формулу в виде отношения, то их можно выразить в любых одинаковых единицах: r₁= R+a₁ = 1,5 cм; r₂ = R+a₂ = 3 cм.

Подставим в формулу (2) значения физических величин и произведем вычисления. Получим: __B.

Диэлектрики в электрическом поле

Пример 1. Две концентрические сферы радиусами 1 см и 2 см несут равномерно распределенные заряды с поверхностными плотностями σ₁ = 0,5 нКл/м² и σ₂ = -1 нКл/м², соответственно. Пользуясь теоремой Гаусса, найти зависимость напряженности электрического поля от расстояния от центра сфер. Объем между сферами заполнен фарфором (e = 6,5).

Пример 2. Металлический шар радиусом 3 см несет заряд 20 нКл. Шар окружен слоем парафина толщиной 2 см. Определить энергию электрического поля, заключенного в слое диэлектрика.

Пример 3. Емкость одного из участков электронной схемы необходимо уменьшить с 3600 до 1000 пФ. Какую емкость необходимо подключить к этому участку, чтобы добиться желаемого результата, ничего более в цепи не изменяя? Как следует подключить дополнительный конденсатор?

Пример 4. Определить емкость сферического конденсатора с радиусами обкладок R₁ = 1,00 см и R₂ = 1,1 см, который заполнен изотропным диэлектриком с относительной диэлектрической проницаемостью, изменяющейся по закону:  = k/r², где k = 0,1 м².