9.Вывод уравнения напора и подачи вихревого насоса.

Выражение напора вихревых насосов показывают с помощью закона о количестве движения жидкости, развернув в виде прямой линии ось бокового канала.

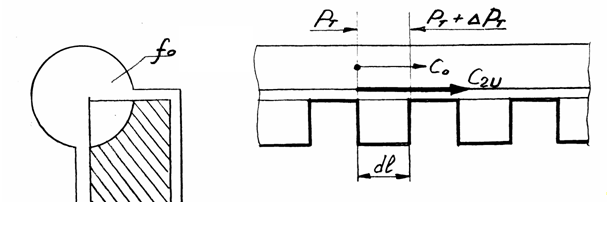
Согласно закону, изменение количества движения секундной массы жидкости между двумя сечениями на участке dl равно сумме сил действую­щих на жидкость между этими сечениями:

1. – количество движения при входе.

2. – количество движения при выходе.

3. – сила давления на жидкость при входе на участок dl.

4. – сила давления на жидкость при выходе с участка dl.

– расход жидкости через межлопастные каналы к единице длинны бокового канала.

C₀ – скорость жидкости.

C_2U – средняя окружная скорость при выходе из колеса.

f – площадь сечения бокового канала.

P_T – давление жидкости при входе на участок dl.

dP_T – приращение давления жидкости на участке dl.

;

;

H_T – теоретический напор насоса;

.

Подача насоса:

;

.

Движение жидкости в проточной части сопровождается интенсивным вихреобразованием и большими гидравлическими потерями:

Г = 0,7

М = 0,9

0 до 0,8

В закрыто-вихревых насосах жидкость из всасывающего патрубка поступает в боковой канал и отводится в нагнетательный патрубок через окна в боковых крышках корпуса насоса.

10.Вывод коэффициента эжекции струйного насоса.

Подачей струйного насоса называют расход жидкости через всасывающий патрубок:

Q=q∙Q_P,

где:

q – коэффициент эжекции,

Q_P – расход рабочей воды.

Смешанная подача насоса:

Q_CM=Q+Q_P.

Подача струйного насоса зависит от коэффициента эжекции q. Выражение для q получают с помощью закона о количестве движения жидкости. Согласно закону, изменение количества движения секундной массы жидкости между двумя сечениями потока равно сумме сил действующих на жидкость между этими сечениями, т. е. силе осевого давления.

В соответствии с определением получаем:

1. Количество движения при входе в сечение 1.

2. Количкство движения при выходе из сечения 2.

3. Силы действующие на жидкость между сечениями 1 и 2 .

P – сила осевого давления.

Поделив обе части этого уравнения на ∙Q_P, получим:

,

т.к. f₁=f₂ и ∆P невелика, следовательно P=0.

После перегруппировки получаем:

.

После решения относительно Q, получаем:

.

– величина малого порядка (скорость перекачиваемой жидкости).

Для эжекторов q=0,5÷6,5.

Характерной особенностью струйных насосов является низкий КПД:

_H=_Г0,25.

Водоструйные насосы могут использоваться для перекачивания любых жидкостей, кроме высоковязких. Низкий КПД объясняется большими гидравлическими потерями на трение и вихреобразование.

11.Вывод уравнения подачи поршневого насоса.

Подача поршневого насоса зависит от площади поршня и от величины его перемещения во время нагнетания.

,

где r – радиус кривошипа;

 – угол поворота кривошипа;

Х_П – текущее значение хода поршня.

Если поршень переместиться на величину dХ_П, то:

,

,

где C – скорость поршня.

,

,

,

.

Подача насоса за один оборот (поршня) коленчатого вала равна объёму цилиндра:

Подача при непрерывном вращении:

.

С учётом кратности действия:

.

Для насосов двух- и четырёхкратного действия учитывается объём, занятый штоком.

Действительная подача:

,

– рабочий объём цилиндра насоса простого действия,

– насоса многократного действия.

Выше показано, что подача поршневого насоса является величиной переменной, т.к. поршень движется с переменной скоростью, а жидкость при нормальных условиях действия неотрывно следует за поршнем. Это можно показать, построив график подачи. Площадка под кривой (0-6’) равна элементарной подаче насосов, следовательно, вся площадь под кривой (0-6’) равна подаче насоса за один ход поршня.

Вывод: подача насоса простого действия – величина переменная, равна Ø в начале и конце хода нагнетания и имеет максимум в средней части хода нагнетания, когда . Подача насоса простого действия отличается неравномерностью.

Неравномерность оценивается величиной отношения:

,

k=1, =3,14

k=2, =1,57

k=3, =1,43

k=4, =1,11

где:

q_MAX – максимальная секундная подача насоса,

q_CP – средняя подача.

Степень неравномерности подачи зависит от кратности действия.

12.Вывод уравнения напора поршневого насоса.

Напором насоса называют приращение энергии, сообщённое насосом единице массы жидкости. Для поршневого насоса это приращение равно разности энергии жидкости и её напора под поршнем во время нагнетания и всасывания:

.

1 – напор жидкости во время нагнетания,

2 – напор жидкости во время всасывания.

При выводе выражения для этих параметров, учитывают переменную скорость движения жидкости, используя уравнение неустановившегося движения жидкости, которое описывает изменение энергии единицы массы жидкости при её движении на участке бесконечно малой длины:

1 – изменение удельной энергии жидкости, т.е. энергии единицы массы невязкой идеальной жидкости, движущейся с постоянной скоростью.

2 – энергия, затрачиваемая на преодоления гидравлических сопротивлений.

3 – энергия инерционных сил, действующих на жидкость.

Напор под поршнем во время всасывания равен сумме бесконечно малых изменений энергии жидкости по всей длине всасывающего тракта, от приёмного отверстия трубопровода до поршня в данной точке его хода, т.е. получается в результате интегрирования уравнения неустановившегося движения:

Интегрирование происходит почленно, а пределы определяются с помощью схемы.

P_A – давления на свободную поверхность жидкости в расходной цистерне;

V_A – скорость жидкости в направлении приёмного отверстия всасывающего трубопровода;

Z_B – высота всасывания;

X_B – текущее значения хода поршня;

S – полный ход поршня;

C – скорость поршня;

– напор под поршнем во время всасывания.

После интегрирования и суммирования результатов, пренебрегая величинами малого порядка, получаем:

,

где:

1 – напор под поршнем при всасывании; 2 – следствие атмосферного давления,

3 – следствие гидравлического давления во всасывающем тракте,

4 – следствие скорости жидкости и гидравлических сопротивлений всасывающего тракта,

5 – сопротивления всасывающего клапана,

6 – следствие действия инерционных сил на жидкость,

3, 4, 5, 6 – факторы определяющие величину напора при всасывании,

W_B – приведённый коэффициент гидравлических сопротивлений вса­сывающего тракта,

l_B – приведённая длина всасывающего тракта.

Решая это уравнения относительно X_B, принимаем во внимание, что:

.

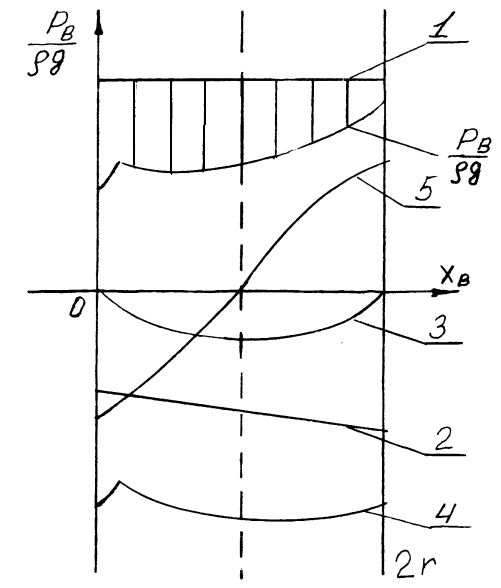
Данные для построения получают в результате суммирования величины составляющих (1-5) с учётом знака.

– величина переменная, имеющая минимум в начале и максимум в конце хода всасывания. Ордината между 1 и – потери жидкости во всасывающем тракте на преодоление его сопротивления.