Приклади

1. Дано дві дискретні випадкові величини X та Y

X = xi	−1	0		Y = yj	0	2	4
p(xi)	0,1	0,9		p(yj)	0,2	0,4	0,4

Побудувати закон розподілу двовимірної випадкової величини (X; Y), якщо випадкові величини X та Y є незалежні.

2. Імовірність появи випадкової події в кожному з чотирьох незалежних екпериментів є величиною сталою і дорівнює 0,9. Розглядаються дві випадкові величини: Х – число появи випадкової події в результаті цих експериментів; Y – число експериментів, при яких подія не наставала. Обчислити .

3. Задано дискретну двовимірну випадкову величину (X; Y):

Y=yj \ X=xi	2	5	8
0,4	0,15	0,30	0,35
0,8	0,05	0,12	0,03

Знайти: а) безумовні закони розподілу випадкових величин X і Y; б) умовний закон розподілу випадкової величини X за умови, що випадкова величина Y набула значення y₁=0,4; в) умовний закон розподілу випадкової величини Y за умови, що випадкова величина X набула значення x₂ = 5.

4. Закон розподілу системи двох дискретних випадкових величин (X;Y) задано таблицею:

Y = yj \ X = xi	5,2	10,2	15,2
2,4	0,1a	2a	0,9a
4,4	2a	0,2a	1,8a
6,4	1,9a	0,8a	0,3a

Знайти а. Обчислити M(X), D(X), (X); M(Y), D(Y), (Y); K_xy, r_xy, P(5,2X<15,2; 2,4< Y  6,4).

5. Задано функцію розподілу двовимірної випадкової величини (X, Y):

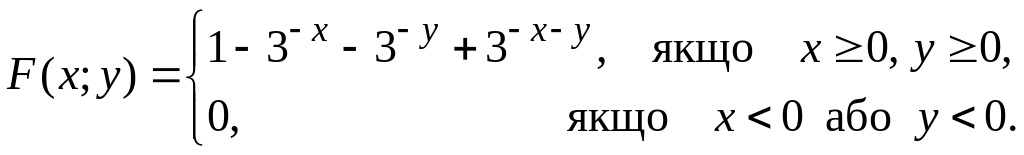
Знайти двовимірну густину розподілу ймовірностей системи (X; Y) та числові характеристики її складових.

6. Густину розподілу ймовірностей системи випадкових величин задано виразом:

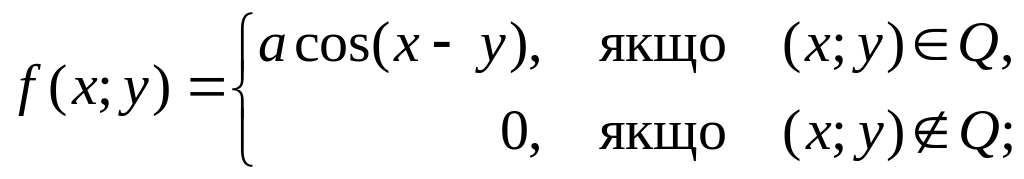
де

Визначити а і . Обчислити

7. Двовимірну випадкову величину задано густиною розподілу ймовірностей:

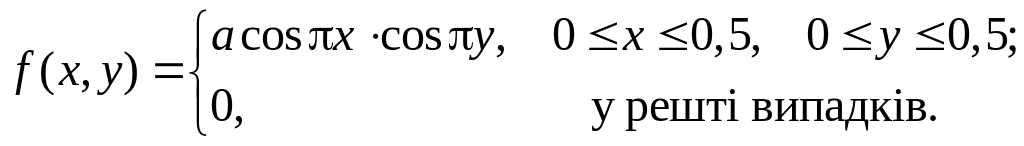
Знайти: а) сталу а; б) умовні густини розподілів складових та їх умовні математичні сподівання.

8. Випадкові величини Х та Y незалежні. Випадкова величина Х розподілена за нормальним законом з параметрами і . Випадкова величина Y рівномірно розподілена на відрізку . Знайти: а) густину ймовірності випадкової величини ; б) функцію розподілу ; в) імовірність .

9.* Незалежні випадкові величини Х і Y задані густинами ймовірностей:

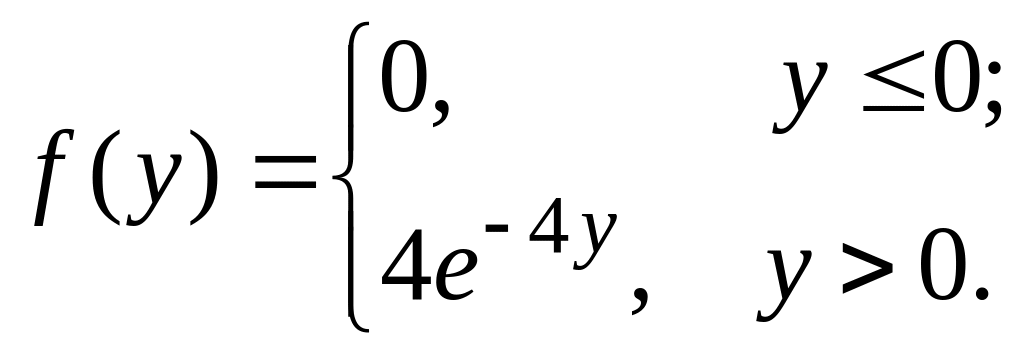
Знайти .

Відповіді: 2. -0,36; -1.

3. а)	Х	2	5	8		Y	0.4	0.8
		0.2	0.42	0.38			0.8	0.2

б)		2	5	8	в)		0.4	0.8
		0.1875	0.375	0.4375			0.714	0.286

4. а = 0,1; M(X) = 9,7; D(X)=17,25; (X) = 4,15; M(Y) = 4,4; D(Y) = 2,4; (Y) = 1,55; K_xy = −2,4; ; P(5,2  X < 15,2; 2,4 < Y  6,4) = 0,49.

5.

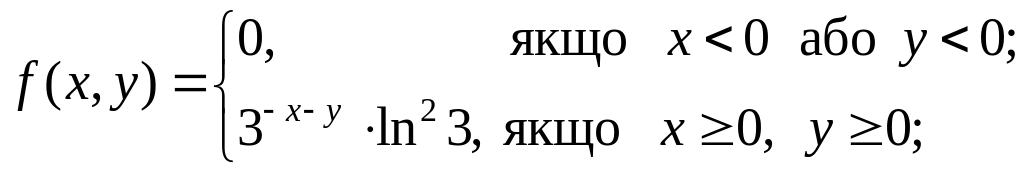
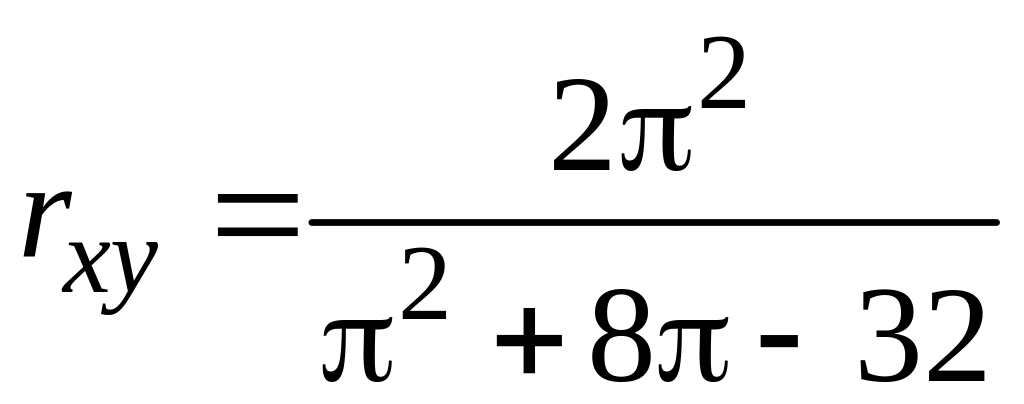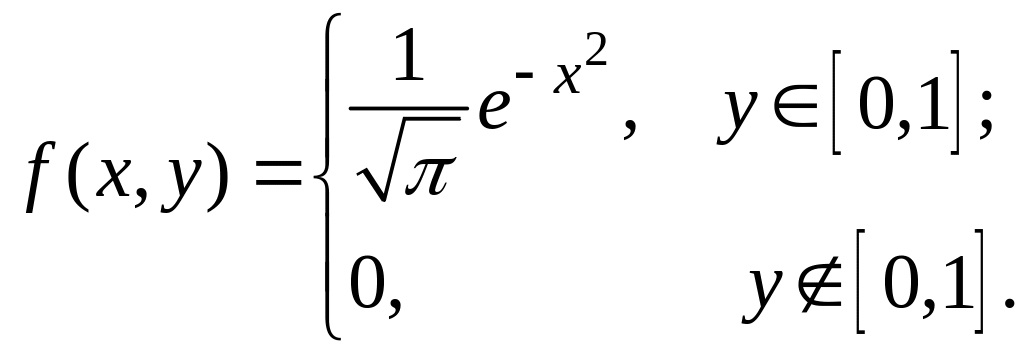; ; . 6. а=0,5; ; 0,25. 7. а) ; б) ; ; ; . 8. а) б) 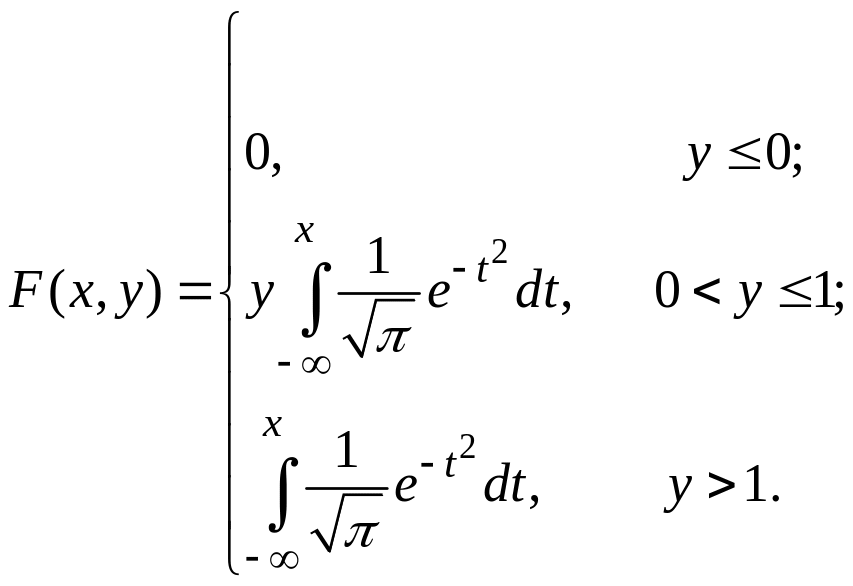в)0,42.9.