2.5.2. Функція двох випадкових аргументів

Нехай X, Y, Z – одновимірні випадкові величини.

Означення. Якщо кожній парі значень випадкових величин Х і Y відповідає одне можливе значення випадкової величини Z, то Z називають функцією двох випадкових аргументів Х і Y:

Далі виникає задача: знайти закон розподілу випадкової величини Z, знаючи сумісний закон розподілу випадкових величин Х і Y. На практиці цю задачу найчастіше потрібно розв’язувати, коли . Ми обмежимося тут розв’язуванням сформульованої задачі для функції .

А. В и п а д о к д и с к р е т н и х а р г у м е н т і в. Якщо Х і Y – дискретні випадкові величини, то випадкова величина також дискретна. Щоб скласти закон розподілу функції Z = X + Y, потрібно знайти можливі значення Z та їх імовірності і записати у відповідну таблицю.

Приклад 2.44. Дискретні незалежні випадкові величини Х і Y задані законами розподілу у формі таблиць:

	1	3			2	4
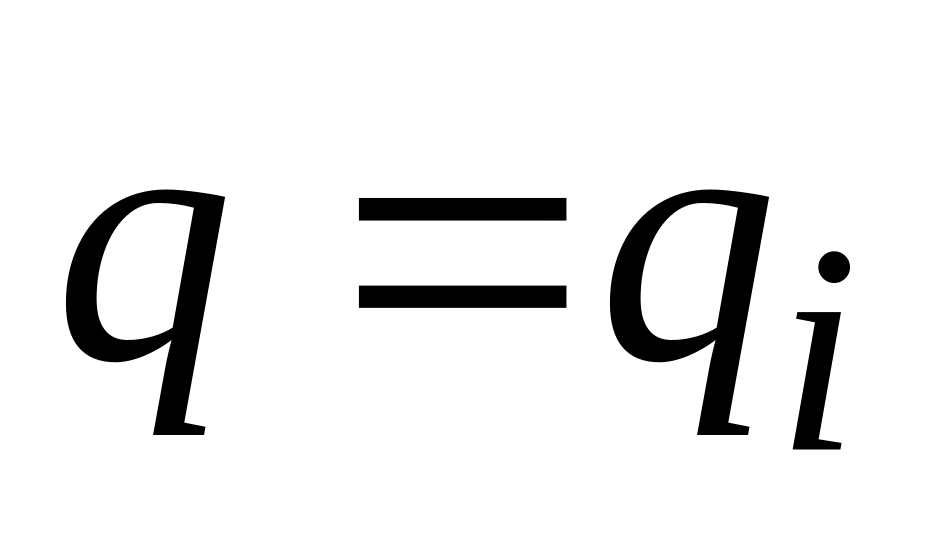
	0,3	0,7			0,4	0,6

Написати закон розподілу випадкової величини

Розв’язання. Можливими значеннями випадкової величини Z є суми кожного мож­ливого значення величини Х із кожним можливим значенням величини Y:

Потрібно ще знайти ймовірності цих можливих значень. Для того, щоб , потрібно, щоб величина Х набула значення і величина Y – значення . А це озна­чає, що подія є добутком подій і . Оскільки випадкові величини Х і Y незалежні, то ймовірність події є добутком імовірностей подій і , а саме: .

У результаті маємо:

;

;

;

.

Перевірка: .

Оскільки два значення і величини Z повторюються, то в таблиці записуємо одне з них, додавши відповідні їм імовірності.

Отже, закон розподілу величини має вигляд:

	3	5	7
	0,12	0,46	0,42

Б. В и п а д о к н е п е р е р в н и х а р г у м е н т і в. Якщо аргументи Х і Y – неперервні випадкові величини, то функція – також неперервна випадкова величина.

Щоб знайти закон розподілу g(z) випадкової величини у випадку незалежних неперервних аргументів Х, Y, користуємося таким правилом: якщо Х і Y незалежні неперервні випадкові величини і густини їх розподілів є функції і , відповідно, то густина розподілу g(z) випадкової величини Z виражається формулами:

(2.83)

або

(2.84)

Формули (2.83), (2.84) називають згорткою, або композицією двох законів.

Приклад 2.45. Незалежні випадкові величини Х і Y задані густинами розподілу:

Знайти густину розподілу g(z) випадкової величини

Розв’язання. За формулою (2.83):

.

Якщо , то і ; якщо , то і . Ураховуючи ці рівності для , далі знаходимо:

, .

Перевірка: тут маємо, що розподіл величини Z зосереджений на проміжку і

.

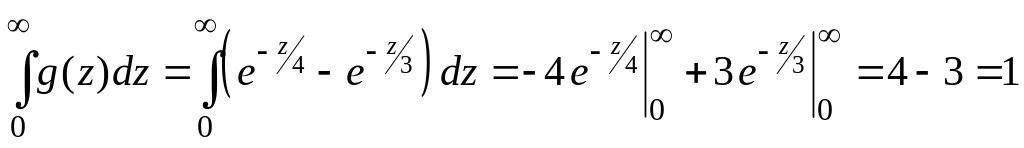Зауваження. Якщо випадкові величини Х і Y не є незалежні, то густина g(z) випадкової величини обчислюється за формулами:

або

де – густина сумісного розподілу Х і Y.