2.5. Функції випадкових аргументів

У цьому підрозділі розглянемо функції, аргументами і значеннями яких є випадкові величини.

2.5.1. Функція одного випадкового аргументу

Нехай Х і Y – дві одновимірні випадкові величини.

Означення. Якщо кожному можливому значенню випадкової величини Х відповідає одне можливе значення випадкової величини Y, то Y називають функцією випадкового аргументу Х:

.

Далі розглянемо, як знайти розподіл імовірностей функції випадкового аргументу за відомим законом розподілу аргументу.

А. В и п а д о к д и с к р е т н о г о а р г у м е н т у. Нехай розподіл випадкової величини Х задано таблицею:

Таблиця 2.10

			…
			…

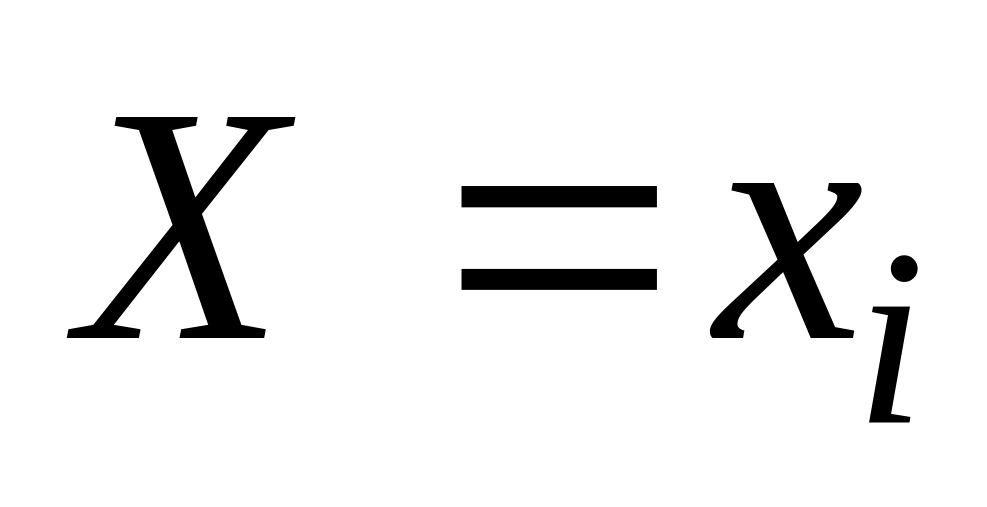
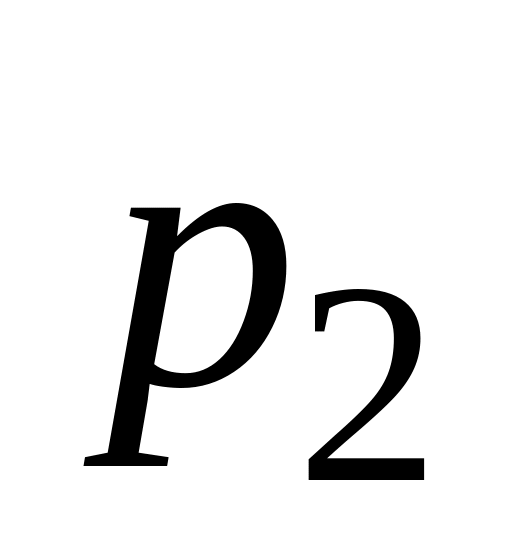
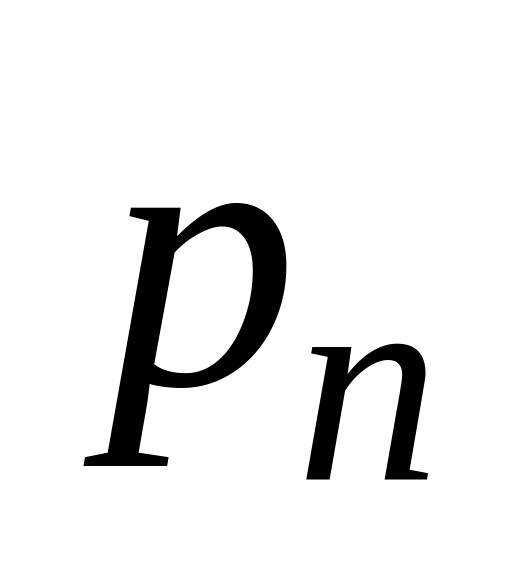
Якщо різним можливим значенням аргументу Х відповідають різні можливі значення функції Y, то ймовірності відповідних значень Х і Y є рівні між собою. Тому закон розподілу випадкової величини має вигляд:

Таблиця 2.11

			…
			…

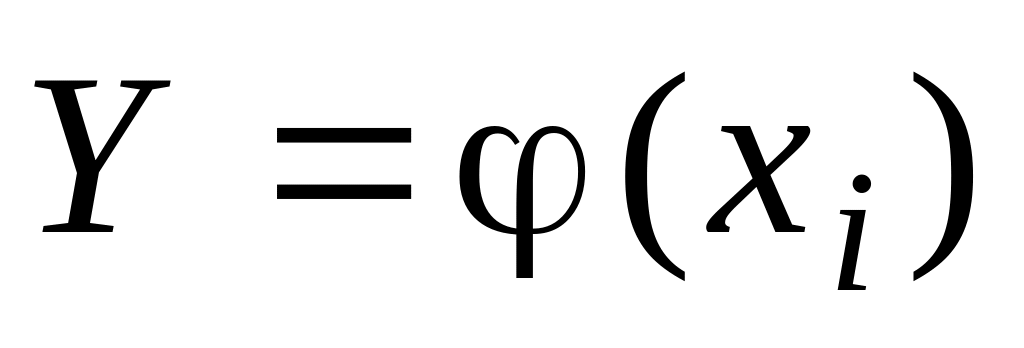
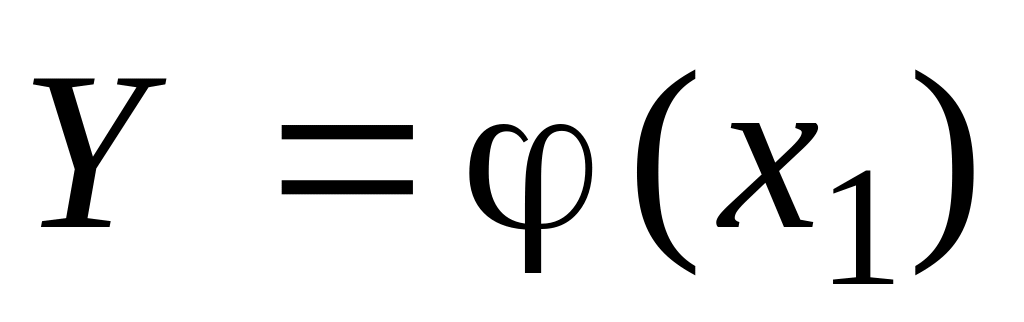
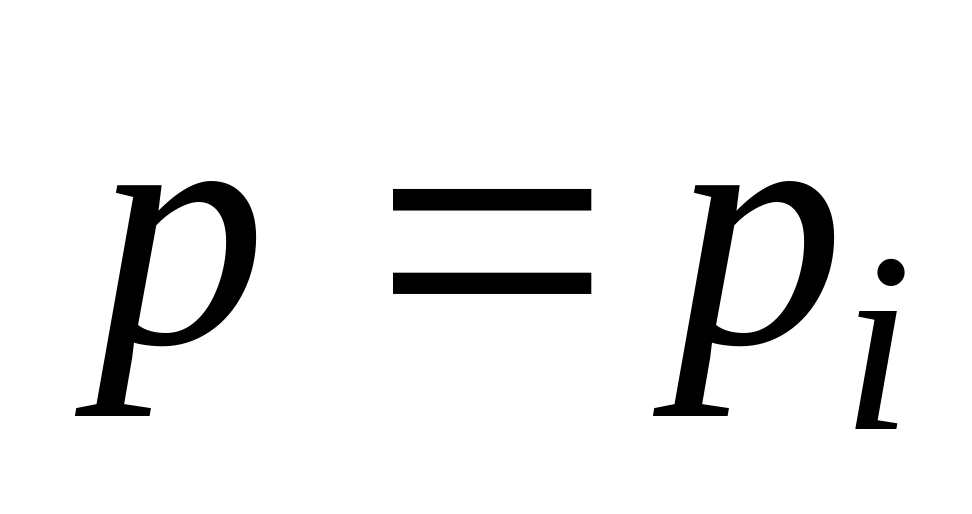
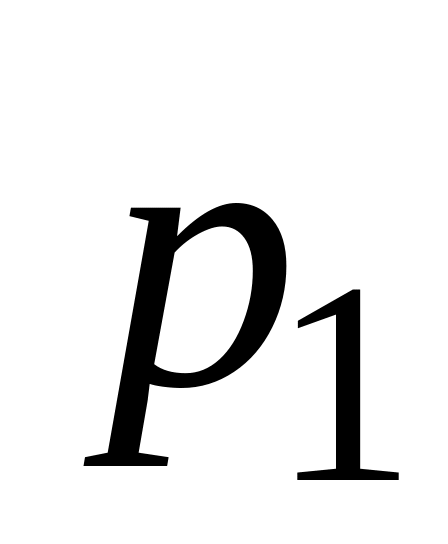
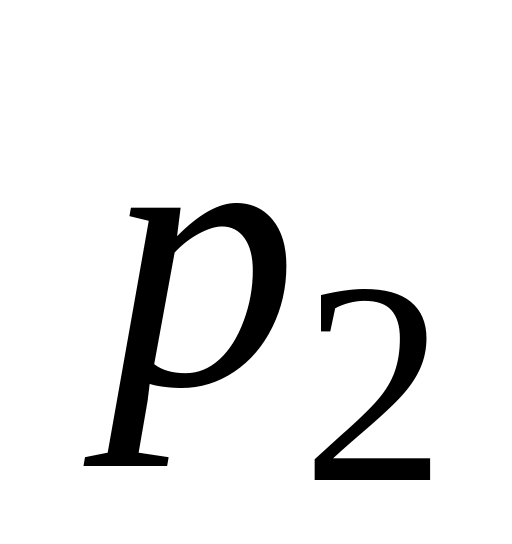
При цьому, якщо в законі розподілу значення функції повто­рюються, то кожне з них записують один раз, додаючи їх імовірності.

Приклад 2.41. Закон розподілу дискретної випадкової величини Х задано таблицею:

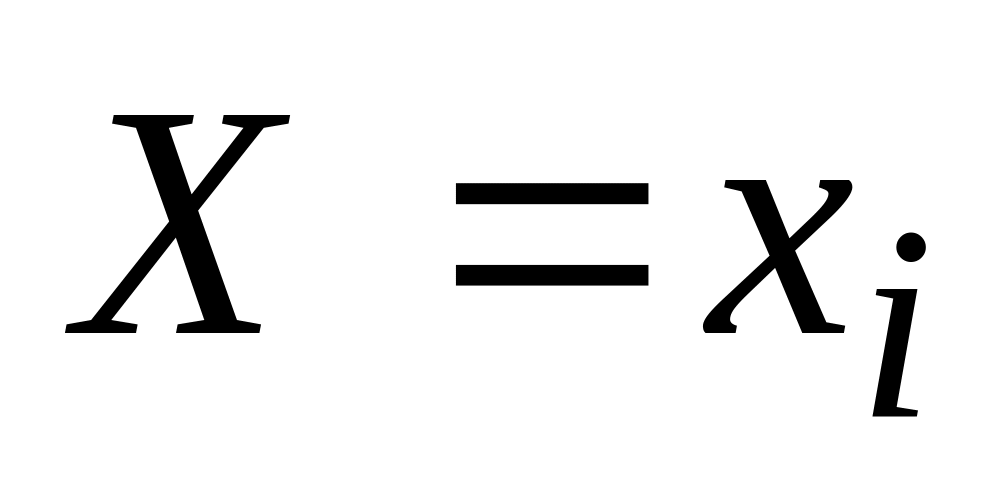
	–3	–1	0	1	3	5
	0,1	0,2	0,1	0,2	0,3	0,1

Написати закон розподілу для функції .

Розв’язання. Із заданої функціональної залежності маємо:

	17	1	–1	1	17	49
	0,1	0,2	0,1	0,2	0,3	0,1

Ураховуючи, що значення 1 і 17 повторюються, знаходимо:

У результаті закон розподілу дискретної випадкової величини має вигляд:

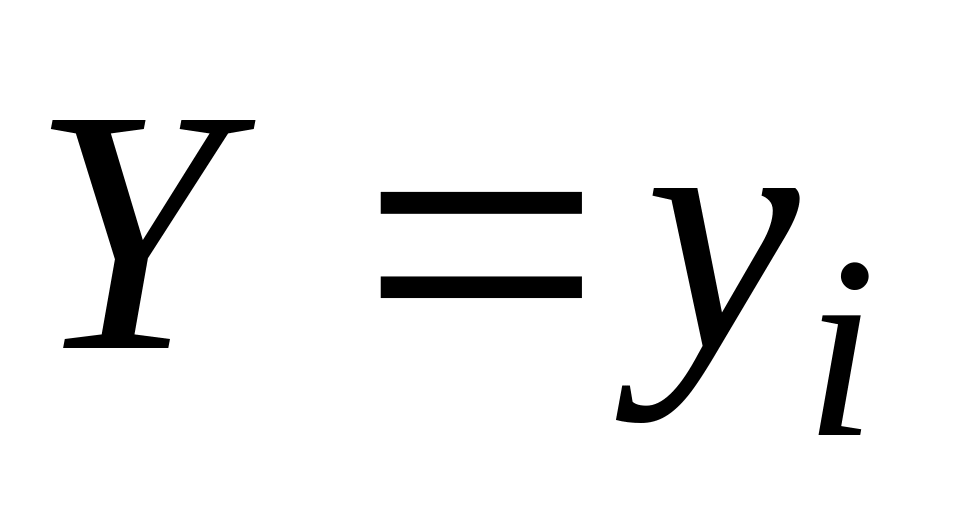
	–1	1	17	49
	0,1	0,4	0,4	0,1

Б. В и п а д о к н е п е р е р в н о г о а р г у м е н т у. Нехай тепер випадкова величина Х неперервна і густина розподілу задана функцією f(x). Розглянемо спочатку випадок, коли функція строго монотонна, неперервна і диференційовна в інтервалі (а, b) усіх можливих значень випадкової величини Х. Дане припущення гарантує існування однозначної оберненої функції для заданої функції .

Тоді існує густина розподілу g(y) випадкової величини , яка визначається рівністю:

. (2.81)

Приклад 2.42. Неперервна випадкова величина Х задана густиною розподілу:

Знайти густину розподілу g(y) для функції .

Розв’язання. Інтервал можливих значень для випадкової величини Y: , бо .

Оскільки задана функція є строго монотонна (зростаюча), то існує обернена до неї функція:

.

За формулою (2.81) маємо, що

.

Отже, густина розподілу g(y) випадкової величини Y має вигляд:

Перевіримо ще виконання умови :

Зрозуміло, що за даною густиною розподілу g(y) випадкової величини можна знайти функцію розподілу G(y) цієї величини за формулою:

.

Зокрема, у даному прикладі при будемо мати:

= + = .

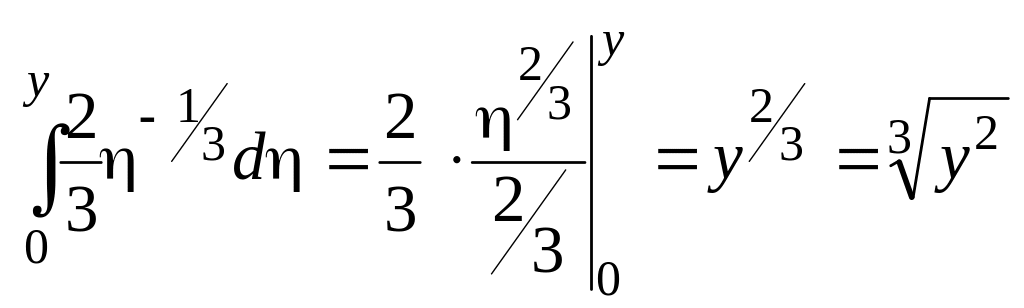Отже, функцію розподілу G(Y) випадкової величини запишемо так:

Припустимо тепер, що функція в інтервалі (а, b) можливих значень випадкової величини Х неперервна, диференційовна, але не є монотонна. У цьому випадку обернена функція неоднозначна.

Число значень оберненої функції залежить від того, яке y ми взяли; позначимо ці значення , , ..., . Тоді густину розподілу g(y) випадкової величини можна визначити за формулою:

(2.82)

де k – число значень оберненої функції, що відповідає одному y, і , , ..., – значення оберненої функції, які відповідають даному y.

Приклад 2.43. Випадкова величина Х задана густиною:

Знайти густину розподілу випадкової величини .

Розв’язання. Можливі значення випадкової величини Y: , бо .

У даному випадку зв’язок між можливими значеннями х і у випадкових величин Х і Y виражаються функцією .

Обернена функція при даному Y має два значення:

, .

Обчислюємо похідні:

, .

За формулою (2.82), маємо:

.

Перевірка:

Отже, густина розподілу випадкової величини виражається рівністю: