
- •Розділ і. Первісна та невизначений інтеграл
- •Властивості невизначеного інтеграла
- •1.1. Таблиця основних інтегралів
- •1.2. Методи інтегрування
- •1.2.1. Метод безпосереднього інтегрування
- •1.2.2. Метод заміни змінної (метод підстановки)
- •Метод інтегрування частинами
- •I. Інтеграли вигляду
- •II. Інтеграли вигляду
- •III. Інтеграли вигляду
- •IV. Рекурентні формули
- •1.3. Інтегрування деяких класів функцій
- •1.3.1. Інтегрування функцій, які містять квадратний тричлен
- •1.3.2. Інтегрування раціональних функцій
- •1.3.3. Інтегрування деяких ірраціональних функцій
- •Іv. Інтегрування біномних диференціалів
- •1.3.4. Інтегрування тригонометричних та гіперболічних функцій
- •Якщо , то використовуємо підстановку .
- •Якщо , то використовуємо підстановку .
- •Якщо , то використовуємо підстановку .
- •V. Інтегрування гіперболічних функцій
- •Розділ іі. Завдання для розрахунково-графічної роботи
1.3.4. Інтегрування тригонометричних та гіперболічних функцій
I.
Інтеграли вигляду
![]() ,
де
,
де
![]() – раціональна функція своїх аргументів
і
– раціональна функція своїх аргументів
і
![]() ,
завжди зводяться до інтегралів від
раціональної функції за допомогою
універсальної тригонометричної
підстановки
,
завжди зводяться до інтегралів від
раціональної функції за допомогою
універсальної тригонометричної
підстановки
![]() .
Звідси отримуємо:
.
Звідси отримуємо:
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Приклад
16. Знайти
інтеграл
![]() .
.
Використовуючи універсальну тригонометричну підстановку, отримуємо
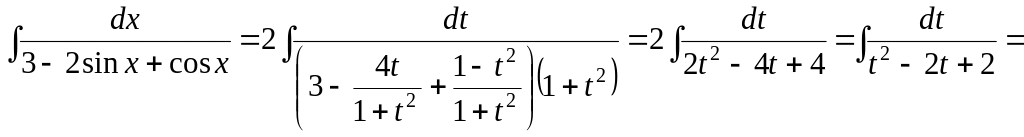
![]() .
.
Універсальна тригонометрична підстановка часто призводить до складних дробово-раціональних функцій. Тому розглянемо інші підстановки:
Якщо , то використовуємо підстановку .
Якщо , то використовуємо підстановку .
Якщо , то використовуємо підстановку .
Приклад 17.
Знайти
інтеграл
![]() .
.
Підінтегральна функція має властивість .
Тому використовуємо
підстановку
,
![]() .
Розділимо чисельник і знаменник
підінтегральної функції на
.
Розділимо чисельник і знаменник
підінтегральної функції на
![]() .
Отримаємо
.
Отримаємо
![]()
![]()
![]() .
.
II.
Інтеграли
![]() ,
,
![]() ,
,
![]() обчислюються з використанням формул
тригонометрії
обчислюються з використанням формул
тригонометрії
![]() ,
,
![]() ,
,
![]()
відповідно.
Приклад
18.
Знайти
інтеграл
![]() .
.
![]()
![]() .
.
ІІІ.
Інтеграли: а)
![]() ,
б)
,
б)
![]() ,
в)
,
в)
![]() ,
г)
,
г)
![]() ,
,
Є різні способи обчислення цих інтегралів. Розглянемо деякі із них.
заміна
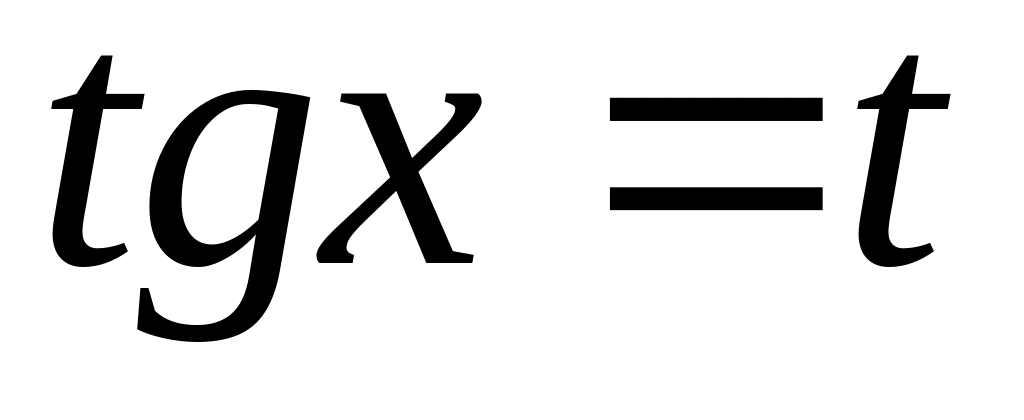 ,
тоді
,
тоді
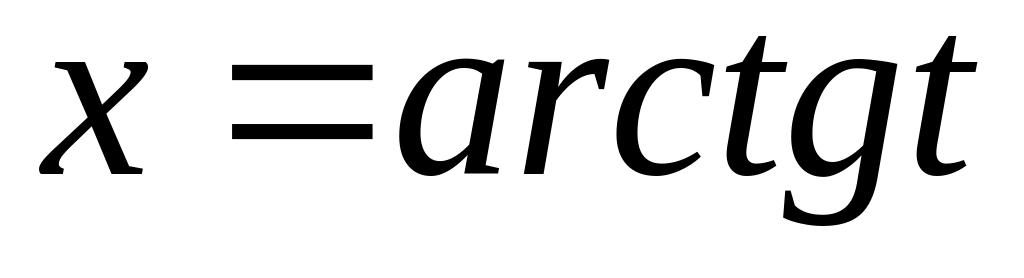 ,
,
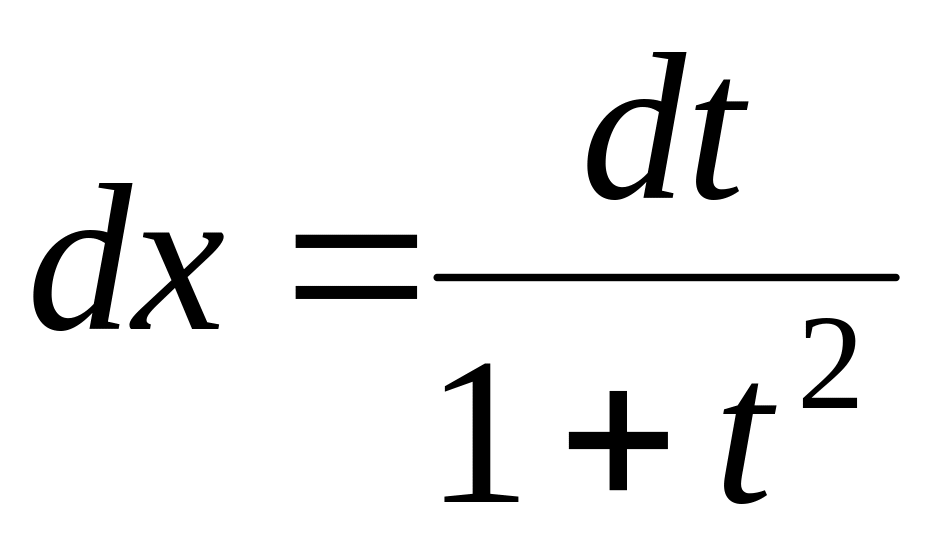 .
Тому
.
Тому
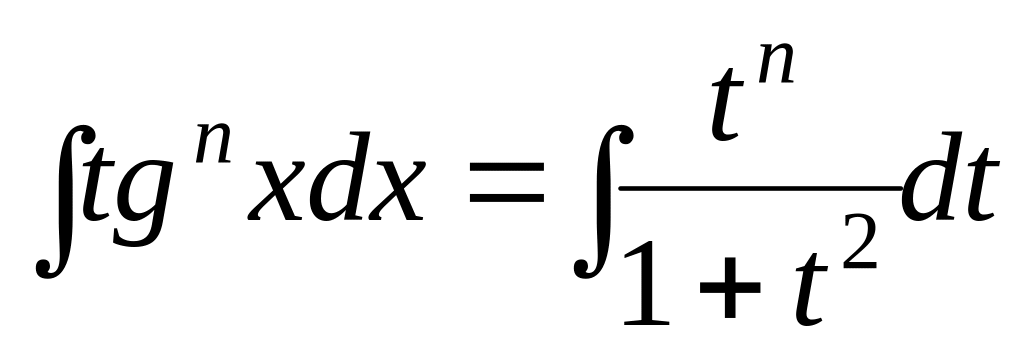 – це інтеграл від раціональної функції,
який розглянуто в 1.3.2.
– це інтеграл від раціональної функції,
який розглянуто в 1.3.2.заміна
 ,
тоді
,
тоді
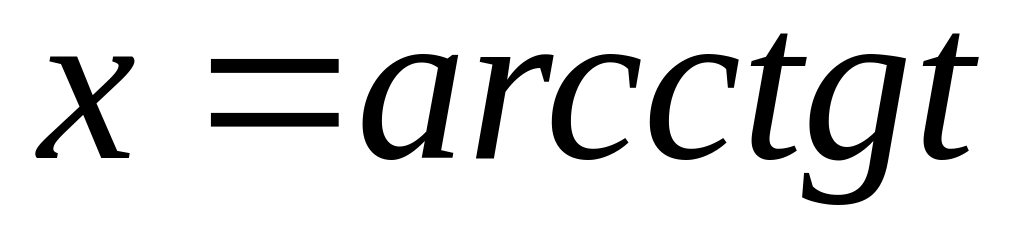 ,
,
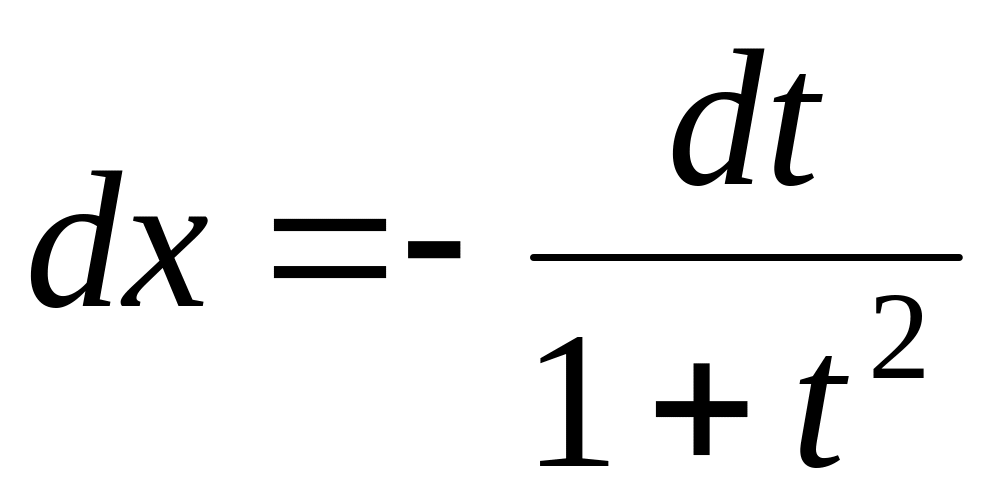 .
Тому
.
Тому
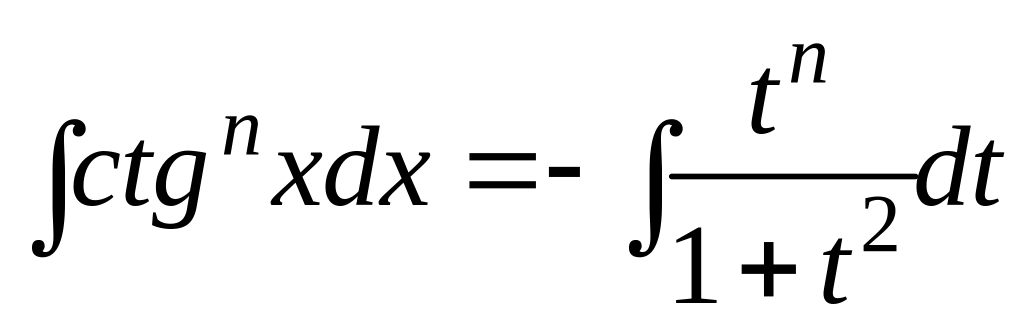 .
.інтеграл просто обчислюється у випадку непарного
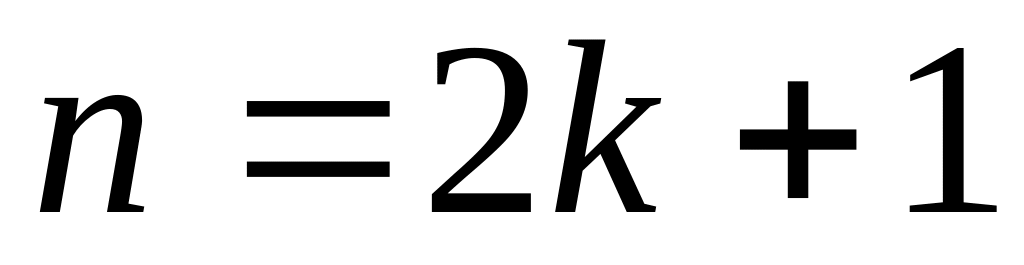 наступним чином:
наступним чином:
![]() – це
– це
інтеграл від
многочлена степеня
![]() .
.
Якщо
![]() ,
то можна скористатись формулою пониження
степеня:
,
то можна скористатись формулою пониження
степеня:
![]() .
.
для цього інтеграла зауваження аналогічні як для випадку в). Якщо , то
![]() .
.
Якщо , то використовуємо формулу пониження степеня:
![]() .
.
Крім того, для інтегралів а) – г) можна отримати рекурентні формули.
Приклад 19.
Знайти інтеграли: а)
![]() ; б)
; б)
![]() .
.
а)
Заміна
,
![]() ,
тоді
,
тоді
![]() ,
.
Тому
,
.
Тому
![]()
![]() .
.
б) Використаємо
формулу пониження степеня:
![]() .
Тоді
.
Тоді
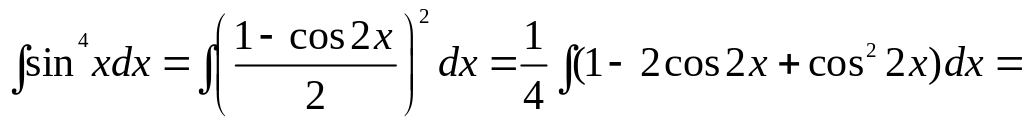
![]()
IV.
Інтеграли вигляду ![]() .
.
Розглянемо такі три випадки:
1. Нехай принаймні одне з чисел чи є непарне натуральне число, наприклад . Тоді
![]()
![]() .
.
А це є інтеграл від многочлена.
2. Нехай та – парні натуральні числа. Тоді використовуємо формули пониження степеня.
3. Нехай
![]() ,
,
![]() .
В
цьому випадку
вигідно використати
підстановку
або
.
В
цьому випадку
вигідно використати
підстановку
або
![]() .
.
Приклад 20.
Знайти
інтеграли: а)
![]() ,
б)
,
б)
![]() .
.
а) Маємо
перший випадок:
![]()
![]()
![]() .
.
б)
Маємо третій випадок:
![]() .
.
![]()
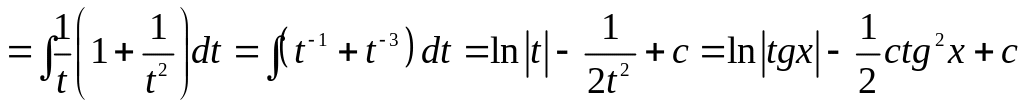 .
.
V. Інтегрування гіперболічних функцій
Чотири основні гіперболічні функції визначаються через експоненту наступним чином
![]() ;
;
![]() ;
;
![]() ;
;
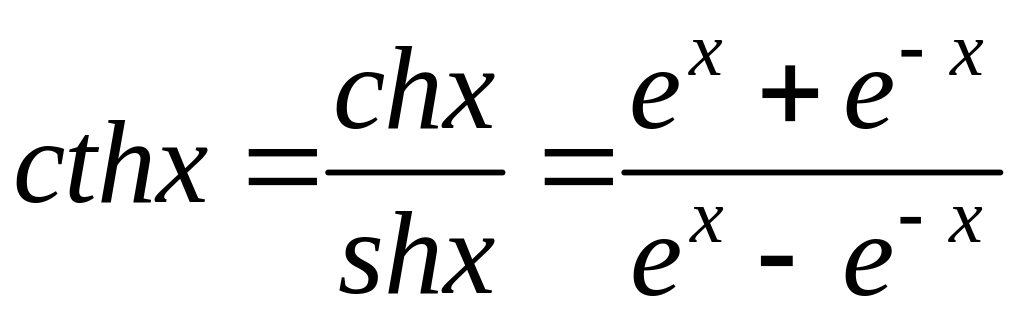 .
.
Крім того, для гіперболічних функцій мають місце формули:
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
; ![]() .
.
Інтеграли від гіперболічних функцій завжди можна звести до інтегралів від експонент, проте іноді отримуємо складні підінтегральні вирази. Не існує загального методу інтегрування гіперболічних функцій.
Інтеграли
вигляду
![]() ,
де
– раціональна функція своїх аргументів
і
,
завжди зводяться до інтегралів від
раціональної функції за до–помогою
підстановки
,
де
– раціональна функція своїх аргументів
і
,
завжди зводяться до інтегралів від
раціональної функції за до–помогою
підстановки
![]() .
Звідси
.
Звідси
![]() ,
,
![]() ,
,
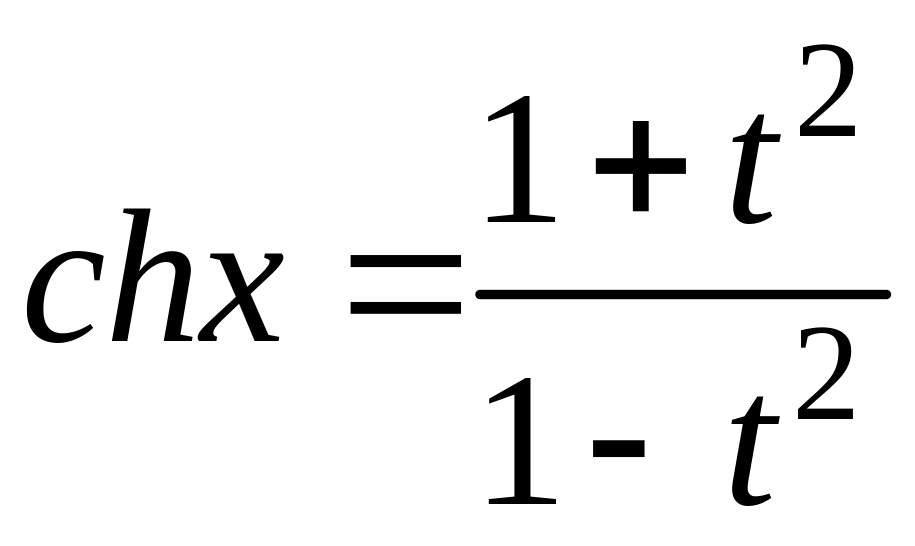 .
.
Якщо
![]() ,
то доцільно використати підстановку
,
то доцільно використати підстановку
![]() .
.
Якщо
![]() ,
то використовуємо підстановку
,
то використовуємо підстановку
![]() .
.
Якщо
![]() ,
то доцільно використати підстановку
,
то доцільно використати підстановку
![]() .
.
Приклад 21. Знайти інтеграли:
а)![]() ; б)
; б)![]() ;
в)
;
в)![]() ;
г)
;
г)![]() .
.
а)
![]()
б)
![]() .
.
в)
![]()
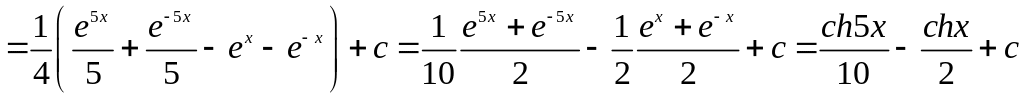 .
.
г) Використаємо формулу інтегрування частинами:
![]()
![]() .
.
Звідси
![]() .
Тому
.
Тому
![]() .
.
