
- •Розділ і. Первісна та невизначений інтеграл
- •Властивості невизначеного інтеграла
- •1.1. Таблиця основних інтегралів
- •1.2. Методи інтегрування
- •1.2.1. Метод безпосереднього інтегрування
- •1.2.2. Метод заміни змінної (метод підстановки)
- •Метод інтегрування частинами
- •I. Інтеграли вигляду
- •II. Інтеграли вигляду
- •III. Інтеграли вигляду
- •IV. Рекурентні формули
- •1.3. Інтегрування деяких класів функцій
- •1.3.1. Інтегрування функцій, які містять квадратний тричлен
- •1.3.2. Інтегрування раціональних функцій
- •1.3.3. Інтегрування деяких ірраціональних функцій
- •Іv. Інтегрування біномних диференціалів
- •1.3.4. Інтегрування тригонометричних та гіперболічних функцій
- •Якщо , то використовуємо підстановку .
- •Якщо , то використовуємо підстановку .
- •Якщо , то використовуємо підстановку .
- •V. Інтегрування гіперболічних функцій
- •Розділ іі. Завдання для розрахунково-графічної роботи
1.3.3. Інтегрування деяких ірраціональних функцій
Інтеграл від довільної ірраціональної функції є, взагалі кажучи, неелементар-ною функцією. Тому лише окремі класи ірраціональних функцій вдається зінтег-рувати в елементарних функціях. Інтегрування ірраціональних функцій здійснюється за допомогою підстановок, які дозволяють інтеграли від ірраціональних функцій звести до інтегралів від раціональних функцій.
Під ірраціональною функцією тут розуміємо явну алгебраїчну ірраціональну функцію – функцію, яку можна отримати шляхом виконання чотирьох арифметичних дій і дії добування кореня, виконаних скінченну кількість разів.
Нехай
![]() – раціональна
функція своїх аргументів.
Розглянемо
інтегрування деяких алгебраїчних
ірраціональностей.
– раціональна
функція своїх аргументів.
Розглянемо
інтегрування деяких алгебраїчних
ірраціональностей.
І.
Інтеграл
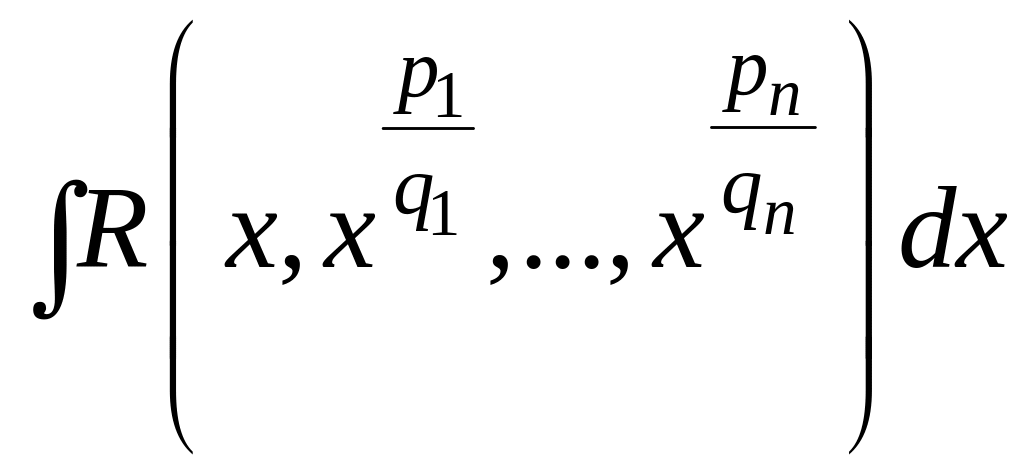 .
Тут
.
Тут
![]() –
раціональні числа,
–
раціональні числа,
![]() .
Заміною
.
Заміною
![]() ,
де
,
де
![]() –
спільний знаменник дробів
,
даний інтеграл зводиться до інтеграла
від раціональної функції.
–
спільний знаменник дробів
,
даний інтеграл зводиться до інтеграла
від раціональної функції.
Приклад 12.
Знайти інтеграл
![]() .
Тут
.
Тут
![]() ,
,
![]() ,
,
![]() .
Спільний знаменник цих дробів
.
Спільний знаменник цих дробів
![]() .
Тому робимо заміну
.
Тому робимо заміну
![]() .
Тоді
.
Тоді
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
Отже,
.
Отже,
![]()
![]() .
.
ІІ. Інтеграл
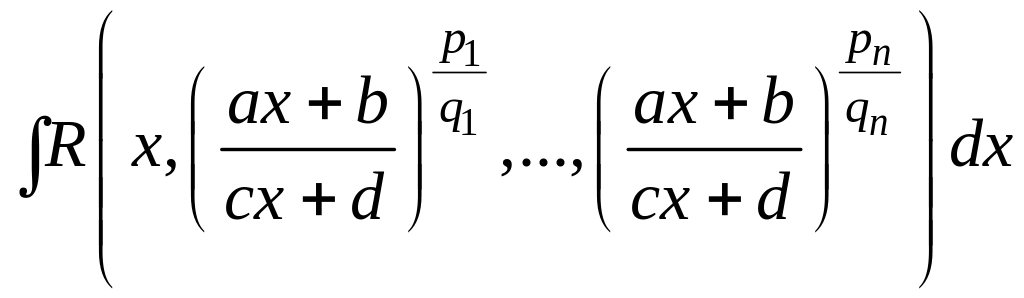 підстановкою
підстановкою
![]() ,
де
–
спільний знаменник дробів
,
зводиться до інтеграла
від раціональної функції.
,
де
–
спільний знаменник дробів
,
зводиться до інтеграла
від раціональної функції.
Приклад 13.
Знайти інтеграл
![]() .
.
Запишемо підінтегральну функцію так:
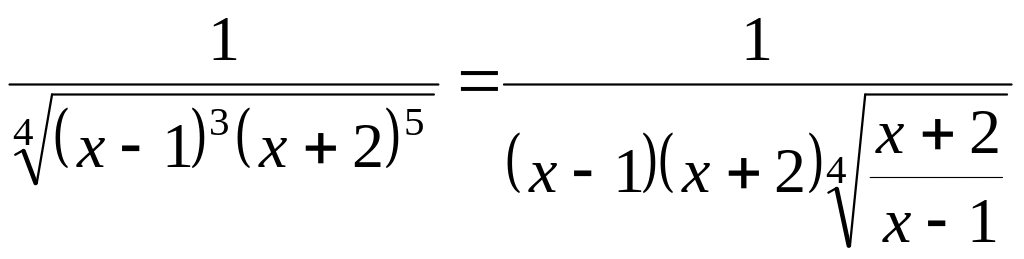 .
.
Тому
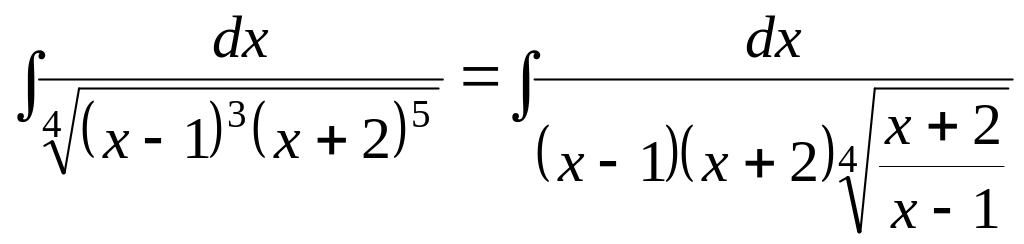 .
Виконаємо підстановку
.
Виконаємо підстановку
![]() .
Тоді
.
Тоді
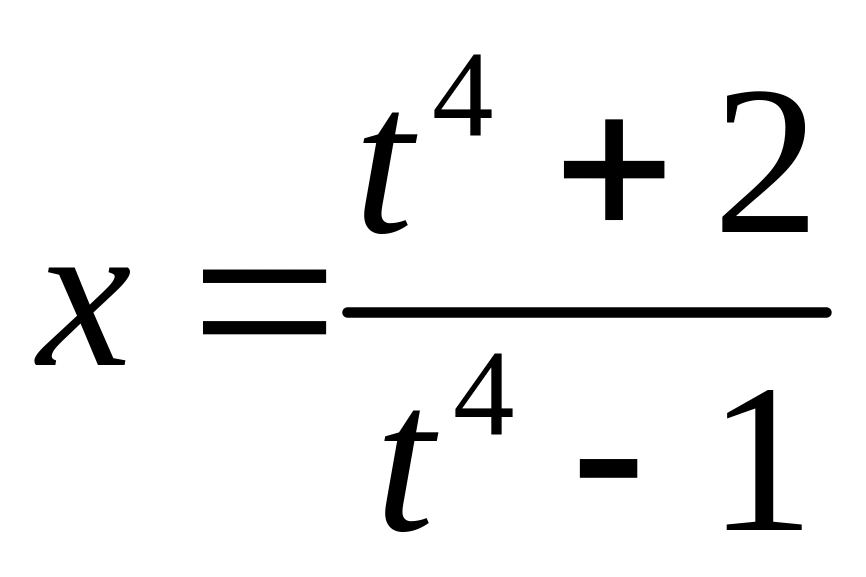 ,
,
![]() ,
,
![]() ,
,
![]() .
Отже,
.
Отже,
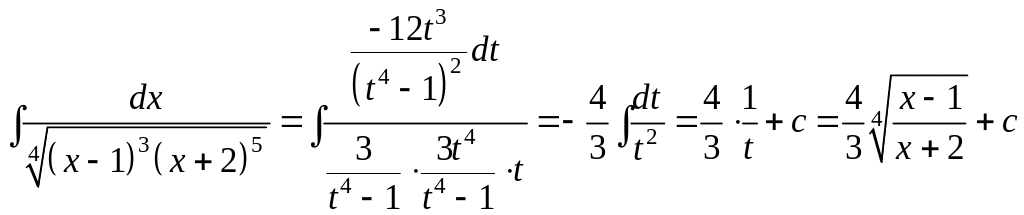 .
.
ІІІ.
Інтеграл
![]() зводиться до інтеграла
від раціональної функції за допомогою
однієї з трьох підстановок Ейлера.
зводиться до інтеграла
від раціональної функції за допомогою
однієї з трьох підстановок Ейлера.
Якщо , то використовується підстановка
 .
.Якщо
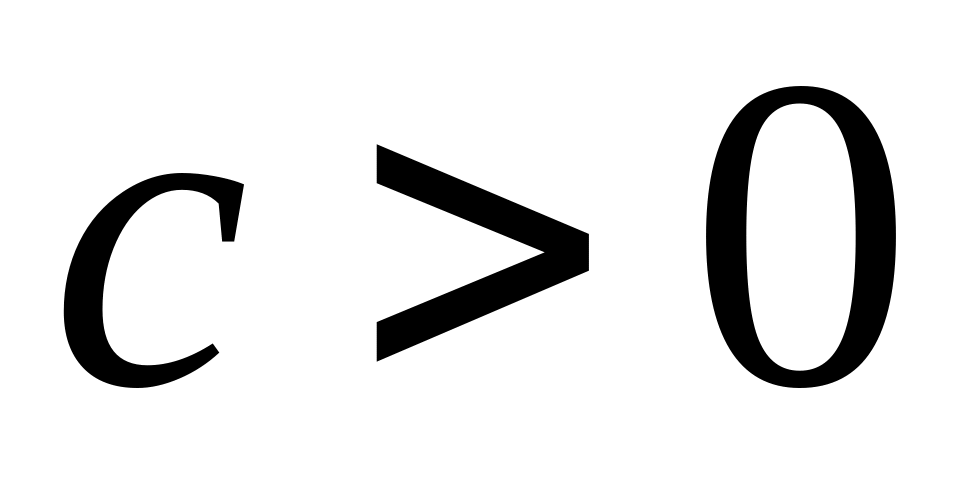 ,
то використовується підстановка
,
то використовується підстановка
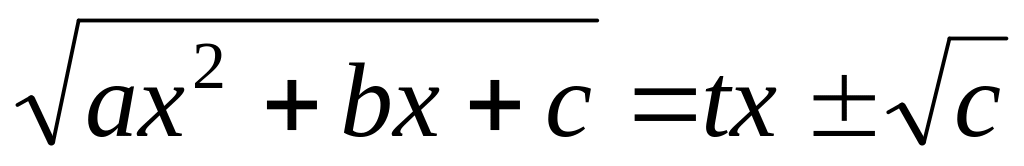 .
.
3. Якщо
![]() –
дійсні корені рівняння
–
дійсні корені рівняння
![]() ,
то використовується підстановка
,
то використовується підстановка
![]() ( або
( або
![]() ).
).
Зауваження.
Оскільки квадратний тричлен
![]() є під знаком квадрат-ного
кореня, то
є під знаком квадрат-ного
кореня, то
![]() .
Якщо
.
Якщо
![]() ,
то рівняння
має
два різні корені, або один кратний корінь
і тому в цьому випадку застосовна третя
підстановка Ейлера. Якщо ж
,
то рівняння
має
два різні корені, або один кратний корінь
і тому в цьому випадку застосовна третя
підстановка Ейлера. Якщо ж
![]() ,
то необхідно
.
Тоді
,
то необхідно
.
Тоді
![]() ,
а тому повинно бути
.
В цьому випадку можна використати першу
або другу підстановку Ейлера. Отже, двох
підстановок Ейлера ( першої і третьої
) досить для інтегрування даного вигляду
інтегралів. Але ми будемо використовувати
всі три підстановки в залежності від
ситуації, яку продемонструємо на такому
прикладі.
,
а тому повинно бути
.
В цьому випадку можна використати першу
або другу підстановку Ейлера. Отже, двох
підстановок Ейлера ( першої і третьої
) досить для інтегрування даного вигляду
інтегралів. Але ми будемо використовувати
всі три підстановки в залежності від
ситуації, яку продемонструємо на такому
прикладі.
Приклад 14.
Знайти інтеграл
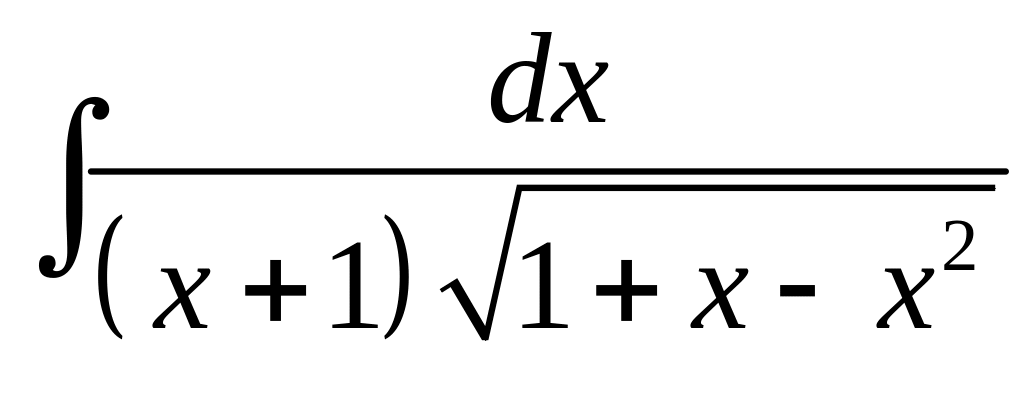 .
.
В даному випадку
![]() ,
,
![]() .
Тому можна застосувати другу підстановку
Ейлера:
.
Тому можна застосувати другу підстановку
Ейлера:
![]() .
Але можна застосувати і третю підстановку
Ейлера, оскільки рівняння
.
Але можна застосувати і третю підстановку
Ейлера, оскільки рівняння
![]() має два дійсні різні корені:
має два дійсні різні корені:
![]() .
Тому з огляду на вигляд
коренів
раціональнішою є саме друга підстановка
Ейлера. Виходячи з неї, отримаємо:
.
Тому з огляду на вигляд
коренів
раціональнішою є саме друга підстановка
Ейлера. Виходячи з неї, отримаємо:
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Тому
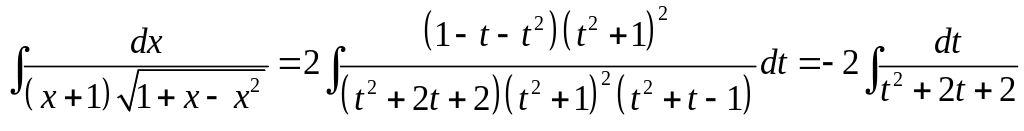 =
=
![]() .
.
На практиці підстановки Ейлера нерідко призводять до громіздких підінтегра-льних виразів. Тому їх слід використовувати лише у випадках, коли інших шляхів нема. Так, зокрема, не раціонально використовувати підстановки Ейлера для таких інтегралів:
![]() ,
,
![]() ,
.
,
.
Ці інтеграли були обчислені нами в п. 1.3.1 іншим способом.
Іv. Інтегрування біномних диференціалів
Розглянемо
інтеграл
![]() від біномного диференціала
від біномного диференціала
![]() ,
де
,
де
![]() –
довільні дійсні числа, а
–
довільні дійсні числа, а
![]() –
раціональні числа. П.Л.Чебишов
довів, що даний інтеграл можна подати
через елементарні функції лише в таких
трьох випадках.
–
раціональні числа. П.Л.Чебишов
довів, що даний інтеграл можна подати
через елементарні функції лише в таких
трьох випадках.
1.
![]() –
ціле: заміна
–
ціле: заміна
![]() ,
де
,
де
![]() –
спільний знаменник дробів
та
.
–
спільний знаменник дробів
та
.
2.
![]() –
ціле: підстановка
–
ціле: підстановка
![]() ,
де
–
знаменник дробу
.
,
де
–
знаменник дробу
.
3.
![]() –
ціле: підстановка
–
ціле: підстановка
![]() ,
де
–
знаменник дробу
.
,
де
–
знаменник дробу
.
Якщо – ціле, то інтеграл від біномного диференціала зводиться до інтеграла І.
Тому розглянемо випадки 2 і 3.
Приклад 15.
Знайти інтеграли: а)
![]() ;
б)
;
б)
![]() .
.
а)
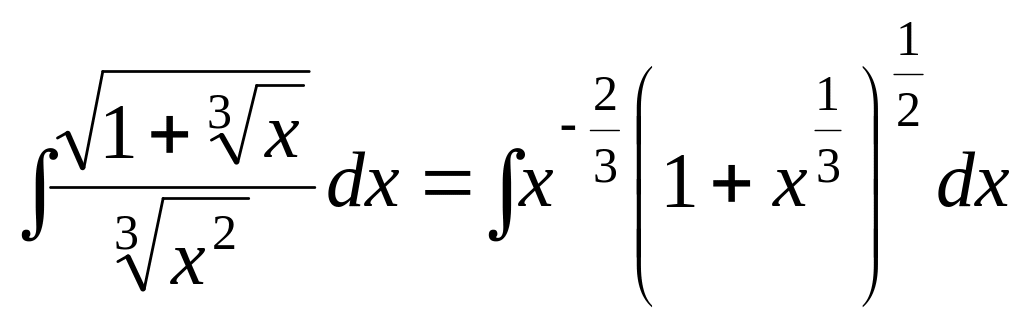 .
Тут
.
Тут
![]() ,
,
![]() ,
,
![]() .
Тоді
.
Тоді
![]() –
ціле. Маємо випадок 2.
Використовуємо підстановку
–
ціле. Маємо випадок 2.
Використовуємо підстановку
![]() .
Звідси
.
Звідси
![]() .
.
Отже,
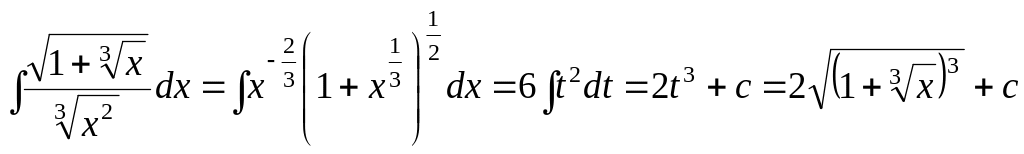 .
.
б)
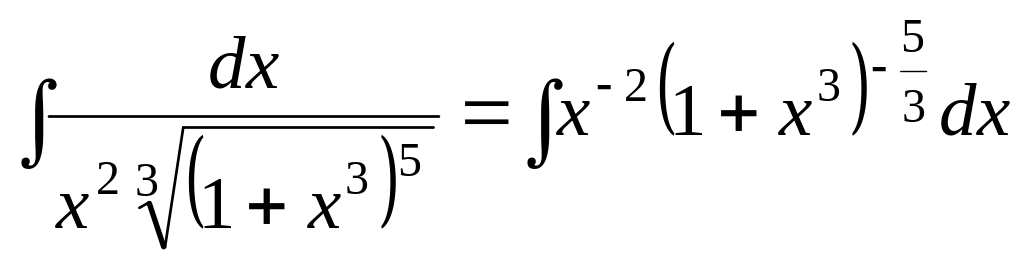 .
В цьому випадку
.
В цьому випадку
![]() ,
,
![]() ,
,
![]() .
Тому
.
Тому
![]() –
не ціле, але
–
не ціле, але
![]() –
ціле. Маємо третій випадок: підстановка
–
ціле. Маємо третій випадок: підстановка
![]() .
Тоді
.
Тоді
![]() ,
,
![]() ,
,
![]() .
.
Отже,

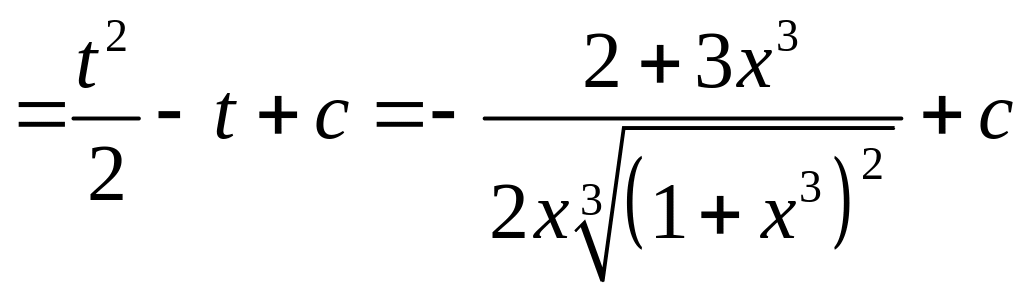 .
.
