4.3. План скоростей

Зависимость между скоростями точек плоской фигуры позво­ляет определять скорости точек этой фигуры простым и наглядным построением, называемым планом скоростей.

План скоростей — это диаграмма, позволяющая графически определить скорости любой точки плоской фи­гуры. План скоростей может быть построен, если известна скорость точки А плоской фигуры и направление скорости другой точки В фигуры или скорость точки А плоской фигуры и мгновенная угловая скорость фигуры.

Пусть известна скорость точки А плоской фигуры и направление скорости точки В (рис. 2.52). Скорость точки С определим с помощью плана скоростей.

Рис. 2.52

Воспользуемся теоремой о скоростях точек плоской фигуры

,

где - скорость полюса; - скорость точки В во вращении вместе с плоской фигурой вокруг полюса А.

Вектор перпендикулярен отрезку АВ, поэтому из произвольного центра О (рис. 2.53) в произвольно выбранном масштабе сначала отложим вектор , затем через концы построенного вектора проведем прямую перпендикулярную отрезку АВ (то есть параллельно вектору вращательной скорости ). Через центр О проведем прямую, параллельную направлению скорости точки В, в пересечении двух проведенных прямых находится точка В, причем вектор будет соответствовать скорости точки В, то есть .

Зная скорости двух точек А и В, найдем скорость третьей, исходя из того, что

и .

Через точки а и b плана скоростей проведем прямые, перпендикулярные АС и ВС соответственно, точка пересечения которых и будет еще одной точкой плана скоростей. Вектор, соединяющий О и с, соответствует скорости точки C

.

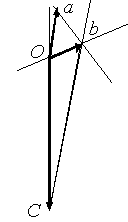
Рис. 2.53

Треугольник abc является планом скоростей, точки а, b, с – вершинами, векторы - лучами. Отрезки, соединяющие вершины плана скоростей (ab,bc,ac), соответствуют скоростям точек В и С при вращении фигуры вокруг соответствующих полюсов ( ). Легко показать, что подобен , поворот происходит в направлении угловой скорости плоской фигуры.

Угловую скорость получим из выражения

или .

Приняв во внимание масштаб построения, можно записать:

.

Задача 2.10. Определить скорость точки D механизма, изображенного на рис. 2.54, а, путем построения плана скоростей, если известно, что угловая скорость стержня равна .

Решение. Скорость точки А будет равна по модулю и направлена, как показано на рисунке. Направление скорости точки В перпендикулярно стержню . Для определения скорости точки D мы сначала должны найти скорость точки С, принадлежащей как стержню АС, так и стержню CD.

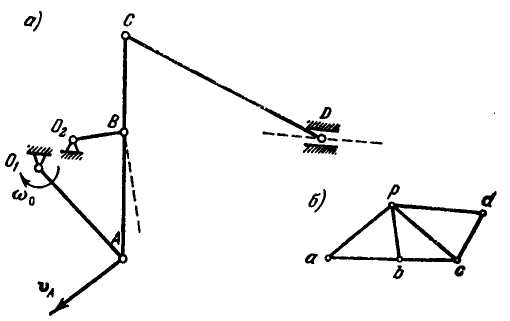
Рис. 2.54

Отложим от полюса р вектор , из точки а проведем прямую, перпендику­лярную стержню АВ (рис. 2.54,6). Прямая, проведенная из точки р параллельно направлению скорости точки В, пересечет прямую, проведенную из точки а, в точке b и, следовательно, вектор будет равен . Точку с на плане скоростей получить путем нахождения точки пересечения прямых линий, проведенных из точки а перпен­дикулярно стержню АС и из точки b перпендикулярно ВС, нельзя, так как эти линии сливаются. Поэтому для нахождения точки с воспользуемся соотношениями:

.

Это значит, что точка b делит отрезок ас в том же отношения, что и точка В — отрезок АС. Таким образом находим точку с. Вектор .

Теперь проведем из точки р прямую, параллельную направлению скорости точки D, а из точки с — прямую, перпендикулярную стержню CD. Пересечение этих прямых определит точку d, причем .