7.4. Модуль и направление кориолисова ускорения

Кориолисовым или поворотным ускорением называется составляю­щая абсолютного ускорения точки в сложном движении, равная удвоен­ному векторному произведению угловой скорости переносного вращения на относительную скорость точки

Кориолисово ускорение характеризует:

1) изменение модуля и направления переносной скорости точки вследствие ее относительного движения;

2) изменение направления относительной скорости точки вследствие вращательного переносного движения.

Модуль кориолисова ускорения определяется как модуль вектор­ного произведения

.

Кориолисово ускорение равно нулю в трех случаях:

1) если , т. е. в случае поступательного переносного движения или в моменты обращения в нуль угловой скорости непоступатель­ного переносного движения;

2) если , т. е. в случае относительного покоя точки или в моменты равенства нулю относительной скорости движущейся точки;

3) если , т.е. в случае, когда ; иначе, когда относительная скорость точки параллельна оси переносного вращения, как, например, при движении точки М вдоль образующей цилиндра, вращающегося вокруг своей оси (рис. 2.102). Направление кориолисова ускорения определяется по правилу вектор­ного произведения (рис. 2.103). Построив условно вектор в точке М, направим кориолисово ускорение по перпендикуляру к плоскости векторов и в ту сторону, откуда поворот вектора к скорости на наименьший угол виден происходящим в сторону, обратную вращению часовой стрелки.

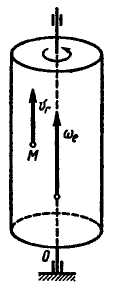
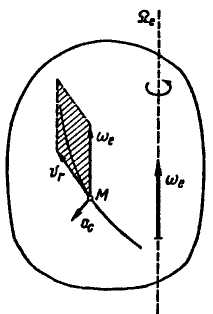
Рис. 2.102 Рис. 2.103

Для определения направления кориолисова ускорения удобно поль­зоваться правилом Жуковского: чтобы найти направление кориолисова ускорения, следует спроецировать относительную скорость точки на плоскость, перпендикулярную оси переносного вращения, и повернуть эту проекцию в той же плоскости на 90° в сторону переносного вращения (рис. 2.104).

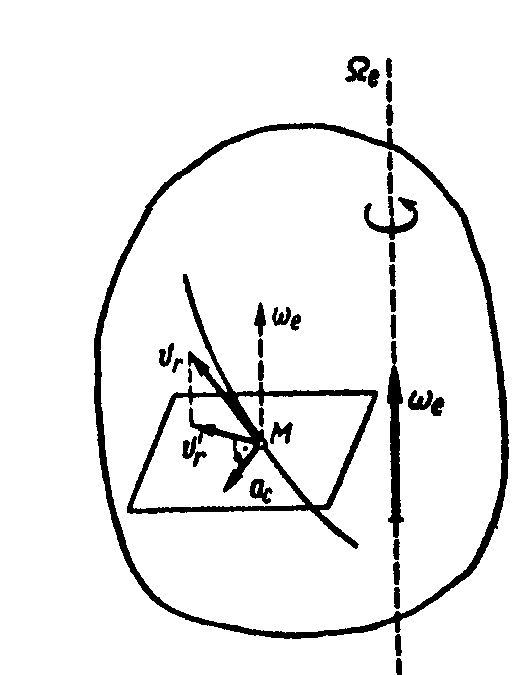
Рис. 2.104

Действительно, полученное направление (рис. 2.104) перпендику­лярно плоскости треугольника, образованного скоростью и ее проекцией , а эта плоскость совпадает с плоскостью векторов и .

Задача 2.21. Клин, движущийся прямолинейно по горизонтальной плоскости с ускорением , перемещает вдоль вертикальных направляющих стержень DE (рис. 2.105). Определить ускорение стержня, если угол клина равен .

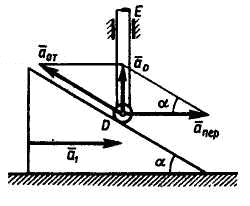
Рис. 2.105

Решение. Абсолютное ускорение точки D стержня направлено по вертикали вверх. Его можно рассматривать как слагающееся из относительного ускорения , направленного вдоль щеки клина, и переносного ускорения , равного ускорению клина (так как переносное движение, т. е. движение клина является поступательным). Строя соответствующий параллелограмм и учитывая, что = , найдем

.

Величина и определяет ускорение стержня.

Задача 2.22. По железнодорожному пути, проложенному по параллели северной широты, движется тепловоз со скоростью v=20 м/с с запада на восток(рис.2.106). Найти кориолисово ускорение тепловоза.

Решение. Свяжем неподвижную систему отсчета с Землей, подвижную систему с тепловозом. Тогда вращение Земли вокруг собственной оси для всех точек тепловоза будет являться переносным, а угловая скорость вращения Земли – переносной угловой скоростью . Скорость движения тепловоза по железнодорожному пути – относительной скоростью .

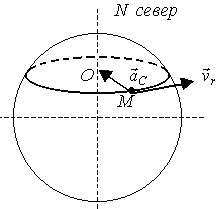
Рис. 2.106

Вектор лежит в плоскости, перпендикулярной оси переносного вращения, и значит угол, образованный вектором переносной угловой скорости и вектором относительной скорости , равен 90^о, а . Тогда

.

Угловая скорость переносного вращения определяется из того, что полный оборот Земля совершает за 24 часа.

.

Ускорение Кориолиса для тепловоза равно 0,29 см/с² и направлено в соответствии с правилом Жуковского к центру окружности той параллели северной широты, по которой движется тепловоз.

Задача 2.23. Диск радиусом R=1 м вращается в плоскости чертежа вокруг неподвижной точки О против хода часовой стрелки по закону (t – в с, - в рад). По ободу диска из точки О движется точка М по ходу часовой стрелки согласно уравнению ( t – в с, s - в м). Определить абсолютную скорость и абсолютное ускорение точки М в момент времени t = 0,5 c (рис. 2.107).

Решение. Точка М совершает сложное движение. Свяжем подвижную систему отсчета с диском. Тогда относительным движением точки М будет ее движение по ободу диска. Это движение задано естественным способом. Переносным движением точки М является движение той точки диска, в которой находится в данный момент рассматриваемая точка М, т.е. вращение диска вокруг оси О.

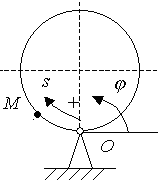
Рис. 2.107

Определим положение точки М в указанный момент времени, при t = 0,5 c

м,

следовательно, к указанному моменту времени точка пройдет четверть окружности. При t = 0,5 c

рад.

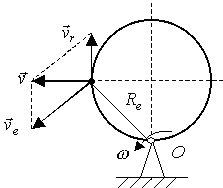
Рис. 2.108

Покажем положение диска и точки, соответствующее заданному времени (рис. 2.108), и определим радиус переносного вращения:

м.

2. Определение абсолютной скорости . По теореме о сложении скоростей

.

Относительное движение задано естественным способом, поэтому воспользуемся формулой для определения

м/с.

На рис. 2.108 в точке М изобразим вектор относительной скорости по касательной к окружности радиусом R в сторону дуговой координаты s, так как . Для определения точки М определим вращательную скорость точки диска, с которой совпадает наша точка М

. (а)

Угловая скорость переносного вращения равна первой производной по времени от угла поворота

213