7.2. Теорема о сложении скоростей при сложном движении точки

Абсолютная скорость точки равна геометрической сумме ее переносной и относительной скоростей.

Эту теорему называют правилом параллелограмма или треуголь­ника скоростей.

Так как абсолютная скорость точки определяется диагональю параллелограмма, построенного на переносной скорости и относи­тельной скорости , то ее модуль можно вычислить по формуле

Задача 2.20. Точка М движется вдоль прямой ОА со скоростью (рис. 2.101), а сама прямая вращается в плоскости Ох₁у₁ вокруг центра О с угловой скоростью . Определить скорость точки М относительно осей Ох₁у₁ в зависимости от расстояния .

Решение. Рассмотрим движение точки М как сложное, состоящее из относительного движения вдоль прямой ОА и движения вместе с этой прямой. Тогда скорость , направленная вдоль ОА, будет относительной скоростью точки. Вращательное движение прямой ОА вокруг центра О является для точки М переносным движением, а скорость той точки т прямой ОА, с которой в данный момент времени совпадает точка М, будет ее переносной скоростью . Так как эта точка прямой движется по окружности радиуса От = r, то по модулю скорость и направлена

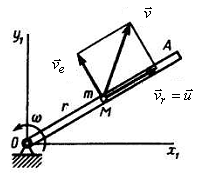
Рис. 2.101

перпендикулярно От. Строя на векторах и параллелограмм, найдем абсолютную скорость точки М по отношению к осям Ох₁у₁. Так как и взаимно перпендикулярны, то по модулю

.

7.3. Теорема о сложении ускорений (теорема Кориолиса)

Для определения абсолютного ускорения точки в случае непоступательного переносного движения воспользуемся выражением абсолютной скорости точки. После ее дифференцирования и преобразования получим

Здесь - кориолисово (поворотное) ускорение точки.

Следовательно,

. (а)

Это равенство выражает теорему Кориолиса (1792-1843) о сложе­нии ускорений в случае непоступательного переносного движения, которая формулируется так: в случае непоступательного переносного движения абсолютное ускорение точки равно геометрической сумме переносного, относительного и кориолисова ускорений.

Таким образом, абсолютное ускорение определяется замыкающей стороной многоугольника ускорений.

В случае поступательного переносного движения = 0, . Так как в этом случае

,

то в случае поступательного пере­носного движения формула (а) принимает вид

Полученный результат является следствием теоремы Кориолиса и формулируется так: в случае поступательного переносного движения абсолютное ускорение точки равно геометрической сумме ее перенос­ного и относительного ускорений.

Таким образом, в случае поступательного переносного движения абсолютное ускорение точки и определяется диагональю параллело­грамма, построенного на двух составляющих ускорениях: переносном , и относительном .

Модуль абсолютного ускорения точки в этом случае можно вычис­лить по формуле

Относительное ускорение , расположено в соприкасающейся пло­скости траектории относительного движения; переносное ускорение - в плоскости, которая параллельна соприкасающейся плоскости траектории полюса О.