2. Задача рівномірного наближення функції.

Як і раніше будемо виходити з таблиці значень функції з п.1. Вище ми розглянули задачу інтерполяції функції, що складалася в заміні даної функції іншої, значення якої в крапці інтерполяції й приймається за наближене значення самої функції. Метод Лагранжа полягає в тому, щоб підміну одного числа іншим виявилося можливим оцінити.

Існує інший підхід, іменований рівномірним наближенням. При цьому підході теж відбувається заміна значення на значення деякої функції , причому виявляється можливим оцінити помилку цієї підміни. Будується функція в такий спосіб.

Для здійснення рівномірного наближення повинна бути задана не тільки таблиця з п.1, але й деякий клас функцій G усередині якого й буде виділена функція . Уведемо величину

,

у якій числа беруться з таблиці в п.1, а числа для кожної функції із класу G передбачаються обчислюваними. Функція вибирається як доставляє мінімум величині . Цю функцію називають найкращим рівномірним наближенням функції із класу G. Звичайно, як оцінити різниця в такій ситуації, - це окрема тема, тісно зв'язана як із природою класу G, так і з таблицею з п.1.

1.4. Метод найменших квадратів.

Припустимо, що клас G являє собою множину всіх багаточленів ступеня не переважаючого деякого конкретного числа m. Тоді задача рівномірного наближення функцій здобуває наступний вид:

серед багаточленів знайти такий, при якому величина

приймає мінімальне значення.

Для цього треба знайти такі , при яких функція приймає мінімальне можливе значення, а це відбувається тоді, коли дорівнюють нулю всі її частки похідні:

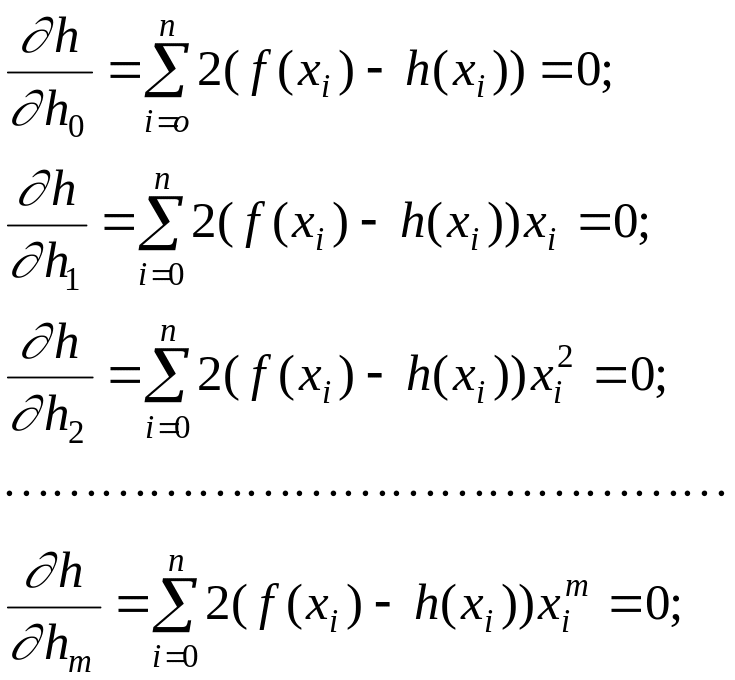
це - система з m+1лінійних алгебраїчних рівнянь із m+1 невідомими ; можна довести, що ця система завжди сумісна й визначена. Її рішенням і є шуканий багаточлен.

Розпишемо цю систему в традиційній формі, розкривши скобки й привівши подібні члени:

;

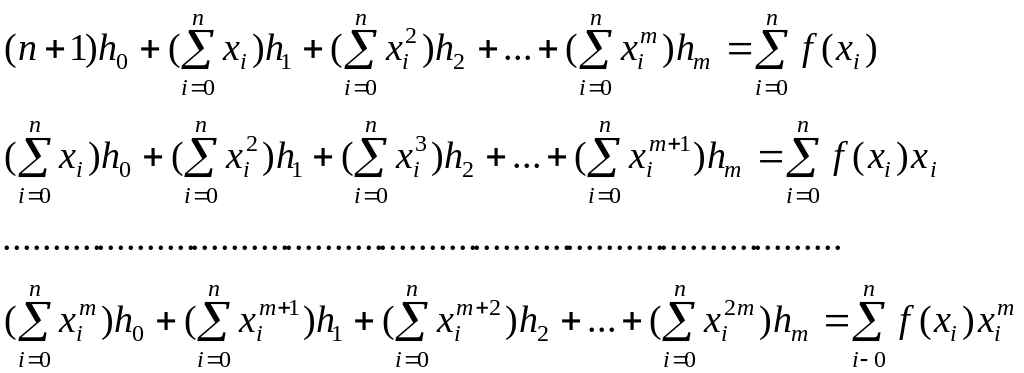включивши процедуру рішення систем лінійних алгебраїчних рівнянь тепер легко одержати відповідь.

2. Багаточлени Бернштейна.

Припустимо, що функція задана у відрізку [0,1] у точках , при деякому фіксованому n. У цьому випадку можна побудувати багаточлен Бернштейна

Можна довести, що при багаточлени прагнуть до функції рівномірно по x; крім того, для будь-якого конкретного цілого має місце граничне співвідношення для похідних:

Нарешті, відомо, що якщо число задовольняє нерівності на всьому відрізку [0,1], те для кожного із цього відрізка виконується нерівність:

.

Це, звичайно, дозволяє оцінювати помилку, що виникає при відповідній інтерполяційній заміні.

Сказане вище для випадку функції один змінної можна узагальнити на випадок двох і більше змінних. Ми обмежимося узагальненням тільки на випадок двох змінних.

Отже, нехай є функція на квадраті

,

причому реально вона задана у вузлах решітки

,

при заздалегідь фіксованих натуральних числах і . Побудуємо по цій інформації наступний багаточлен від двох змінних:

,

де - біноміальні коефіцієнти. Це - багаточлен Бернштейна для заданої функції на заданих решітці. З його допомогою так само можна здійснювати інтерполяцію, приймаючи його значення в тій або іншій точці квадрата за значення самої функції. Можна довести, що для будь-якої точки квадрата має місце нерівність:

,

яке й дозволяє оцінити погрішність інтерполяції. Тут константи й задовольняють у розглянутому квадраті нерівностям

.

Зауваження. Випадок один змінної розглядався вище на відрізку [0,1], а випадок двох змінних - в одиничному квадраті. У дійсності, розгляди можливі на будь-якому відрізку [a,b] і на будь-якому прямокутнику [a,b;c,d]. Для цього у вихідній ситуації (тобто на довільному відрізку або на довільному прямокутнику) потрібно зробити лінійну заміну змінних. Докладніше: нехай функція задана в точках відрізка , де при деякому фіксованому

Покладемо

тоді

якщо тепер у покласти , то виникне ситуація функції , заданої вже на відрізку [0,1]. Аналогічно, у випадку двох змінних треба зробити заміну

,

після чого виникне ситуація одиничного квадрата.