Геометрический закон распределения

Последовательно проводится несколько независимых испытаний до появления некоторого события  , вероятность которого в каждом испытании одна и та же и равна  . Тогда число   произведённых испытаний есть дискретная случайная величина с геометрическим распределением вероятности. Примером может служить стрельба по некоторой цели до первого попадания, причём вероятность попадания при каждом выстреле не зависит от результатов предыдущих выстрелов и сохраняет постоянное значение  . Число   произведённых выстрелов будет случайной величиной, возможные значения которой являются все натуральные числа. Геометрический закон распределения задаётся формулой

 где 

Характеристическая функция геометрического закона распределения задаётся формулой

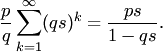
Основные характеристики геометрического закона распределения (математическое ожидание и дисперсия):

Равномерный закон распределения

Равномерное распределение задаётся следующим законом:

Этот закон имеет место в случае, когда   возможных исходов испытания равновероятны. Примером целочисленной случайной величины, распределённой по равномерному закону, может служить число очков, выпадающих при бросании симметричной кости (любое из значений   выпадает с одинаковой вероятностью  ). Характеристическая функция равномерного закона задаётся формулой

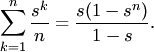
Числовые характеристики геометрического закона распределения (математическое ожидание и дисперсия):

Гипергеометрический закон распределения

Случайная величина   имеет гипергеометрическое распределение с параметрами   и   (  — натуральные числа), если она принимает конечное множество натуральных значений   соответственно с вероятностями

причём  .

Гипергеометрическое распределение возникает в экспериментах по выбору без возвращения   шаров из урны, содержащей   шаров, из которых   белых и   чёрных. Таким образом, это распределение описывает осуществление признака в выборке без возврата (в отличии от биномиального распределения). На практике к гипергеометрическому распределению приводят задачи, где изделия из партии отбирают случайно (обеспечивая для каждого изделия равную возможность быть отобранным), но отобранные изделия не возвращают в партию. Такой отбор особенно важен в тех задачах, где проверка изделия связана с его разрушением (например, проверка изделия на срок службы).

Числовые характеристики гипергеометрического распределения (математическое ожидание и дисперсия):

Следует заметить, что если   очень велико по сравнению с  , то не имеет существенного значения, возвращаются шары обратно или нет, и формула (7.4) может быть приближённо заменена формулой (7.1) биномиального распределения.

19

Правило трёх сигм ( ) — практически все значения нормально распределённой случайной величины лежат в интервале   Более строго — не менее чем с 99,7 % достоверностью значение нормально распределенной случайной величины лежит в указанном интервале (при условии, что величина   истинная, а не полученная в результате обработки выборки).

Если же истинная величина   неизвестна, то следует пользоваться не σ, а s. Таким образом, правило 3-х сигм преобразуется в правило трех s.

20.

Неравенство Чебышева в теории вероятностей утверждает, что случайная величина в основном принимает значения, близкие к своему среднему. Говоря более точно, оно даёт оценку вероятности, что случайная величина примет значение, далёкое от своего среднего. Неравенство Чебышева является следствием неравенства Маркова.