29. Дифференциал функции и его геометрический смысл. Инвариантность формы дифференциала 1-го порядка.

Понятие дифференциала и его геометрический смысл

Пусть функция  определена на промежутке  и дифференцируема в окрестности точки ,тогда  или по теореме о связи бесконечно малых с пределами функций имеем , где  - бесконечно малая величина при . Отсюда:

.          ( 7.1)

Таким образом, приращение функции  состоит из двух слагаемых:

1)  - линейного относительно , т.к. ;

2)  - нелинейного относительно , т.к. .

Определение. Дифференциалом функции называется главная, линейная относительно  часть приращения функции, равная произведению производной на приращение независимой переменной:

.            ( 7.2)

Пример. Найти приращение функции  при  и :

Решение. ,

Пример. Найти дифференциал функции .

Решение. По формуле (7.2.) имеем .

Определение. Дифференциал независимой переменной  равен приращению этой переменной:

          ( 7.3)

Тогда формулу (7.2) для дифференциала функции можно записать в виде:

                  ( 7.4)

Откуда , поэтому  можно рассматривать не только как символическое обозначение производной, но и как обычную дробь с числителем  и знаменателем .

Геометрический смысл. На графике функции  (рис. 7.1.) возьмем произвольную точку . Дадим аргументу  приращение , тогда функция получает приращение . В точке  проведем касательную, образующую угол  с осью . Из треугольника : . Из  имеем: . Таким образом,  и соответствует формуле (7.1).

Следовательно, с геометрической точки зрения дифференциал функции есть приращение ординаты касательной, проведенной к графику функции  в данной точке, когда  получает приращение .

Свойства дифференциала аналогичны свойствам производной.

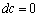
1)	4)
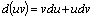
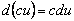
2)	5)
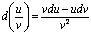
3)

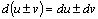
Инвариантность формы дифференциала

Если , то из (7.4) имеем .

Рассмотрим сложную функцию , где .

Если функции  и  дифференцируемые функции от своих аргументов, то производная сложной функции равна .

Умножим обе части равенства на : . Таким образом, .

Это равенство означает, что формула дифференциала не изменится, если вместо функции от независимой переменной  рассматривать функцию от зависимой переменной . Это свойство дифференциала получило название инвариантности (т.е. неизменности) формы дифференциала.

30. Понятие первообразной функции. Неопределенный интеграл и его свойства (одно из свойств доказать).

Понятие первообразной и неопределенный интеграл

Определение. Функция  называется первообразной функцией для функции  на промежутке , если в каждой точке этого промежутка .

Пример.  является первообразной для , т.к. .

Можно заметить, что если для функции  существует первообразная , то она не является единственной. Возвращаясь к примеру, видно, что и функции ,  и вообще  (  - некоторое число) являются первообразными для функции . Таким образом можно сформулировать следующую теорему.

Теорема. Если  и  - первообразные для функции  на некотором промежутке , то найдется такое число , что будет справедливо равенство:

.

Из данной теоремы следует, что, если  - первообразная для функции , то выражение вида , где  - произвольное число, задает все возможные первообразные для .

Определение. Совокупность всех первообразных функции  на промежутке  называется неопределенным интегралом от функции  и обозначается , где  - знак интеграла,  - подынтегральная функция,  - подынтегральное выражение.

Таким образом:

,

где  - некоторая первообразная для ,  произвольная постоянная.

Определение. Операция нахождения неопределенного интеграла называется интегрированием этой функции.

Свойства неопределенного интеграла

1)       Производная от неопределенного интеграла равна подынтегральной функции, т.е. .

□ Доказательство. Дифференцируя левую и правую части равенства , получаем: .■

2)       Дифференциал неопределенного интеграла равен подынтегральному выражению, т.е. .

□ Доказательство. По определению дифференциала и свойству 1 имеем: ■

3)       Неопределенный интеграл от дифференциала некоторой функции равен этой функции с точностью до постоянного слагаемого, т.е. .

□ Доказательство. Рассматривая функцию  как первообразную для некоторой функции , можно записать:  и на основании  дифференциал неопределенного интеграла , откуда .■

4)       Постоянный множитель можно выносить за знак интеграла, т.е. , где  - некоторое число.

5)       Интеграл от алгебраической суммы двух функций равен такой же сумме интегралов от этих функций, т.е. .

Некоторые табличные интегралы

,
,			,

Пример.  Найти .

Решение.

Пример.  Найти .

Решение. = .