21. Теоремы Ролля и Лагранжа (без доказательства). Геометрическая интерпретация этих теорем.

Теорема 1. (Теорема Ролля) Пусть функция f(x)

1. непрерывна на отрезке [a, b];

2. дифференцируема в интервале (a, b);

3. на концах отрезка [a, b] принимает равные значения.

Тогда существует точка c О (a, b) такая, что f'(c) = 0.

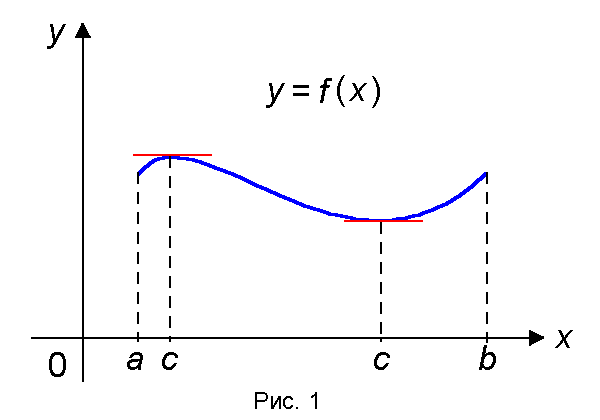
Геометрическая интерпретация теоремы Ролля

Из теоремы Ролля следует, что существует точка с О (a, b), в которой касательная к графику функции f(x) параллельна оси ОX (рис. 1).

Теорема 2. (Теорема Лагранжа) Пусть функция f(x)

1. непрерывна на отрезке [a, b];

2. дифференцируема в интервале (a, b).

Тогда существует точка с О (a, b) такая, что

 

f(b) − f(a) = f '(c) · (b − a) .

(1)

 

Формула (1) называется формулой Лагранжа, или формулой конечных приращений

Доказательство приведено в книге И.М. Петрушко и Л.А. Кузнецова “Курс высшей математики: Введение в математический анализ. Дифференциальное исчисление.” М.: Изд–во МЭИ, 2000. Стр. 119.

Геометрическая интерпретация теоремы Лагранжа

Представим формулу (1) в виде

 

f(b) − f(a) b − a   = f '(c) .

(2)

 

Число  

f(b) − f(a)

b − a

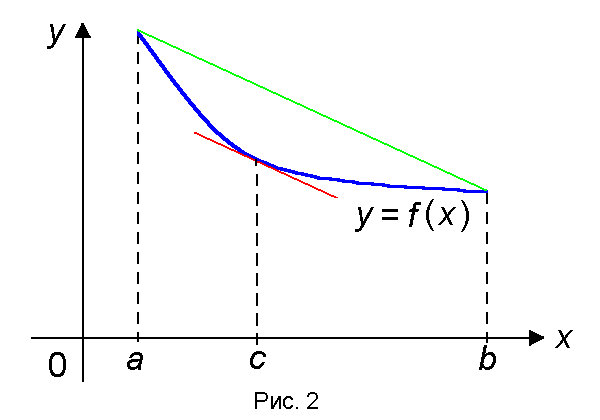
  есть угловой коэффициент прямой, проходящей через концы графика функции y = f(x) — точки (a, f(a) ) и (b, f(b) ), а f '(c) — угловой коэффициент касательной к этому графику в точке (c, f(c) ). Из формулы (2) следует, что существует точка с О (a, b), в которой касательная к графику функции f(x) параллельна прямой, проходящей через концы графика (или совпадает с ней) (рис. 2).

22. Достаточные признаки монотонности функции (график см. стр. 127 учебника)

y=f(x) называется монотонной (возраст. или убыв.) на промежутке М, если для любых двух значений,таких, что х2>x1

Если  f ’( x ) > 0  в каждой точке интервала ( a, b ), то функция  f ( x ) возрастает на этом интервале.

Если  f ’( x ) < 0  в каждой точке интервала ( a, b ) , то функция  f ( x ) убывает на этом интервале

Исследование функций с помощью производных

Условия монотонности функции на интервале

Рассмотрим сначала достаточные условия строгой монотонности функции на интервале.

Теорема 22.1. Для того чтобы дифференцируемая на интервале (a;b) функция   возрастала (убывала) на этом интервале достаточно, чтобы производная   была положительной (отрицательной) всюду на этом интервале.

Доказательство. Рассмотрим случай, когда  . Пусть x1 и x2 - любые две точки интервала (a;b), удовлетворяющие условию  . На отрезке   функция   дифференцируема, а, следовательно, непрерывна. Поэтому к ней можно применить формулу Лагранжа:

  , где  .

По условию  . Поэтому   или  , т.е. функция   возрастает на интервале (a;b). Случай, когда  , рассматривается аналогично.

Теорема доказана.

Из последней теоремы следует, что отличие от нуля производной является достаточным условием строгой монотонности функции. Однако это условие не является необходимым. Так, например, функция   возрастает на любом интервале действительной оси, но при x=0 производная этой функции обращается в нуль (рис. 6). Следующая теорема устанавливает необходимое и достаточное условие монотонности функции.

воторой вариант : Достаточные признаки монотонности ф-ций (один из них доказать).

Теорема (достаточное условие возрастания ф-ции). Если производная дифференцируемой ф-ции положительна внутри некоторого промежутка Х, то она возрастает на этом промежутке.

Рассм х₁ и х₂ на данном промежутке Х. Пусть х₂>х_1,х_1,х₂єХ. Докажем, что f(x₂)>f(x₁).Для ф-ции f(x) на отрехке [x₁;x₂] выполняются условия т. Лагранжа, поэтому f(x₂)-f(x₁)=f ^/(Е)(x₂-x₁), где х₁<Е>х_2, т е Е є промежутку, на кот производная положительна, следов. f^/(Е)>0 и правая часть равенства lim_{x→xo(x→∞)} f(x)/g(x)= lim_{x→xo(x→∞)} f^/(x)/g^/(x)- положительна. f(x₂)-f(x₁)>0 и f(x₂)>f(x₁).

Теорема (достаточное усл убывания ф-ции): Если производная дифференцируемой ф-ции отрицательна внутри некоторого промежутка Х, то она убывает на этом промежутке.

23. Определение экстремума функции одной переменной. Необходимый признак экстремума (доказать).

Опр.экстремума ф-ции одной пер-ной.

Экстремум-это максимум и минимум ф-ции.

Опр1:Точка х₀ наз-ся точкой максимума ф-ции f(x),если в некоторой окрестности точки х0 выполняется неравенство f(x)≥f(x₀).

Опр2:Точка х₁ наз-ся точкой максимума ф-ции f(x),если в некоторой окрестности точки х₁ выполн-ся неравенство f(x)≤f(x1).

Значения ф-ции в точках х₀ и х₁ наз-ся соотв-но максимумом и минимумом ф-ции. Максимум и минимум ф-ции объединяются под общим названием экстремума ф-ции.

На одном промежутке ф-ция может иметь несколько экстремумов,причём может случиться, что минимум в одной т-ке больше максимума в другой f_min(x₂)>f_max(x₀),см. рис.

Необходимое усл-е экстремума.

Для того, чтобы ф-ция y=f(x) имела экстремум в точке х₀, необходимо, чтобы её производная в этой точке равнялась 0 (f’(x₀)=0) или не существовала.

Точки, в кот.выполнено необх.усл-е экстремума,т.е. производная равна нулю или не сущ-ет, наз-ся критическими (или стационарными). Эти точки должны входить в обл.определения ф-ции.(Если в точке х₀ дифференцируемая функция y=f(x) имеет экстремум, то в нек-ой окрестности этой точки выполнены условия тео-мы Ферма, и, следовательно, производная фун-и в этой точке равна нулю.Т.е.f’(x₀)=0. Но фун-я может иметь экстремум и в точках, в которых она не дифференцируема.)

Первое достаточное условие экстремума. Теорема. Если при переходе через точку х₀ производная диф-мой фун-и y=f(x) меняет свой знак с плса на минус, то точка х₀ есть точка максимума фун-и y=f(x), а если с минуса на плюс, - то точка минимума.

Доказательство. Пусть производная меняет знак с плюса на минус, т.е. в некотором интервале (а, х₀) производная положительна (f’ (x) >0), а в некотором интервале (х₀, b) – отрицательна (f’ (x) < 0). Тогда в соответствии с достаточным условием монотонности функции f(x) возрастает на интервале (а, х₀) и убывает на интервале (х₀, b). По определению возрастающей функции f(x₀) > f(x) при всех х принадлежащем (а, х₀), а по определению убывающей функции f(x) < f(x₀) при всех х принадлежащем (х₀, b), т.е. f(x₀)≥f(x) при всех х принадлежащем(а, b), следовательно, х₀ – точка максимума функции y=f(x).

Второе достаточное условие экстремума. Теорема. Если первая производная f’(x) дважды дифференцируемой функции равна нулю в некоторой точке х₀, а вторая производная в этой точке f”(x₀) положительна, то х₀ есть точка минимума функции f’(x); если f”(x₀) отрицательна, то в x₀ – точка максимума.

Доказательство. Пусть f’(x₀) =0, а f” (x₀) >0. Это означает, что f” (x) = (f’(x₀))’ >0 также и в некоторой окрестности точки х₀, т.е. f’(x) возрастает на некотором интервале (a, b), содержащую точку х₀. Но f’(x₀) =0, следовательно, на интервале (а, х₀) f’ (x) >0, т.е. f’ (x) при переходе через точку х₀ меняет знак с минуса на плюс, т.е. х₀ – точка минимума.

24. Достаточные признаки существования экстремума (доказать одну из теорем).

Тео-ма (достаточное условие возр.фун-и). Если производная диф-мой фун-и положительна внутри некоторого промежутка Х, то она возр.на этом промежутке.Док-во: Рас-трим два знач-я x₁ и x₂ на данном промежутке Х. Пусть x₂>x₁, x₁,x₂ принадл-ит Х.Докажем, что f(x₂)>f(x₁). f(x₂)-f(x₁)=f’(a)(x₂-x₁),где х₁<a<x₂ => f’(a)>0. Отсюда f(x₂)-f(x₁)>0 и f(x₂)>f(x₁).

Тео-ма (достаточное условие убыв.фун-и). Если производная диф-мой фун-и отрицательна внутри некоторого промежутка Х, то она убывает на этом промежутке.

25. Понятие асимптоты графика функции. Горизонтальные, наклонные и вертикальные асимтоты. Примеры.

Опр. Асимптотой гра-ка фун-и y=f(x) наз-ся прямая, обладающая тем свой-вом, что расстояние от точки (x, f(x)) до этой прямой стремится к нулю при неограниченном удалении точки графика от начала координат.

Теорема 1. Пусть функция y=f(x) определена на некоторой окрестности точки х₀ (исключая, возможно, саму эту точку) и хотя бы один из переделов функции при х-> х₀ +0 (справа) равен бесконечности, т.е. lim при х стремящимся к х₀ –(+) 0 = бесконечность. Тогда прямая х=х₀ является вертикальной асимптотой графика функции y=f(x).

Теорема 2. Пусть фун-я y=f(x) определена при достаточно больших х и сущ. конечный предел фун-и lim при х стремящимся к бесконечности f(x) = b. Тогда прямая y=b есть горизонтальная асимптота графика фун-и y=f(x).

Теорема 3. Пусть фун-я y=f(x) определена при достаточно больших х и существует конечные пределы lim при х стремящ-ся к беско-ти f(x)/x = k и lim прия х стремящ-ся к беско-ти [f(x) – kx] = b. Тогда прямая y=kх+b явл-ся наклонной асимптотой графика фун-и y=f(x).