Вопросы для самопроверки по дисциплине «Математика (Модуль 1)»

1. Понятие матрицы. Виды матриц. Транспонирование матрицы. Равенство матриц. Алгебраические операции над матрицами: умножение на число, сложение, умножение матриц.

2. Определители 2, 3 и n-го порядков (определения и их свойства). Теорема Лапласа о разложении определителя по элементам строки или столбца.

3. Квадратная матрица и ее определитель. Особенная и неособенная квадратные матрицы. Присоединенная матрица. Матрица, обратная данной, и алгоритм ее вычисления.

4. Система п линейных уравнений с п переменными (общий вид). Матричная форма записи такой системы. Решение системы (определение). Совместные и несовместные, определенные и неопределенные системы линейных уравнений.

5. Решение системы n линейных уравнений с п переменными методом Гаусса.

6. Решение систем п линейных уравнений с п переменными с помощью обратной матрицы (вывод формулы Х=А ^–1В).

7. Теорема и формулы Крамера решения системы п линейных уравнений с п переменными (без вывода).

8. Понятие функции, способы задания функций. Область определения. Четные и нечетные, ограниченные, монотонные функции. Примеры.

функция это «закон», по которому каждому элементу одного множества (называемому областью определения) ставится в соответствие некоторый элемент другого множества (называемого областью значений).

Математическое понятие функции выражает интуитивное представление о том, как одна величина полностью определяет значение другой величины. Так значение переменной x однозначно определяет значение выражения x², а значение месяца однозначно определяет Функция — математическое понятие, отражающее связь между элементами множеств. Можно сказать, что значение следующего за ним месяца, также любому человеку можно сопоставить другого человека — его отца. Аналогично, некоторый задуманный заранее алгоритм по варьируемым входным данным выдаёт определённые выходные данные.

Часто под термином «функция» понимается числовая функция; то есть функция которая ставит одни числа в соответствие другим. Эти функции удобно представляются на рисунках в виде графиков.

Способы задания:Явный( аналитический, описательный),Графический,Табличный

Область определения функции — множество, на котором задаётся функция

Чётность

Основная статья: Нечётные и чётные функции

• Функция 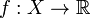называется нечётной, если справедливо равенство

• Функция f называется чётной, если справедливо равенство

1.Ограниченность функции.

Функция f(x) называется ограниченной на данном промежутке (a,b), если существуют некоторые числа m и M такие, что

m ≤ f(x) ≤ M

при хє(a,b).

Число m_o= inf {f(x)} [x є (a,b)] = max m называется нижней гранью функции ,

а число M_o= sup {f(x)} [x є (a,b)]=min M называется верхней гранью функции на данном промежутке (a,b).

Разность M_o- m_o называется колебанием функции на промежутке (a,b).

Моното́нная фу́нкция — это функция, приращение которой не меняет знака, то есть либо всегда неотрицательное, либо всегда неположительное. Если в дополнение приращение не равно нулю, то функция называется стро́го моното́нной. Монотонная функция — это функция, меняющаяся в одном и том же направлении.

Функция возрастает, если большему значению аргумента соответствует большее значение функции. Функция убывает, если большему значению аргумента соответствует меньшее значение функции.

9. Понятие элементарной функции. Основные элементарные функции и их графики (постоянная, степенная, показательная, логарифмическая).

Элементарные функции — функции, которые можно получить с помощью конечного числа арифметических действий и композиций из следующих основных элементарных функций:

• алгебраические:

  • степенная;

  • рациональная.

• трансцендентные:

  • показательная и логарифмическая;

  • тригонометрические и обратные тригонометрические.

Каждую элементарную функцию можно задать формулой, то есть набором конечного числа символов, соответствующих используемым операциям. Все элементарные функции непрерывны на своей области определения.

Иногда к основным элементарным функциям относят также гиперболические и обратные гиперболические функции, хотя они могут быть выражены через перечисленные выше основные элементарные функции.

Постоянная функция.

Постоянной называется функция, заданная формулой у = b, где b - некоторое число.

Графиком постоянной функции у = b является прямая, параллельная оси абсцисс и проходящая через точку (0; b) на оси ординат. На рисунке изображены графики нескольких постоянных функций. В частности, графиком функции y = 0 является ось абсцисс.

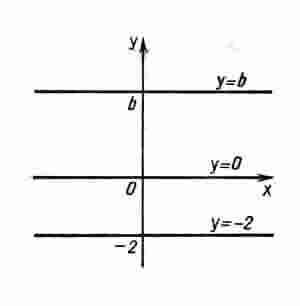
Если b = 0, то получаем прямую пропорциональность у = kх.

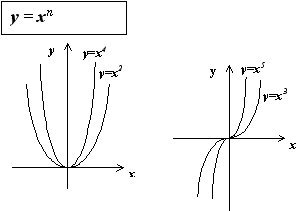
Степенной функцией с вещественным показателем a называется функция y = x ⁿ , x > 0.

Заметим, что для натуральных n степенная функция определена на всей числовой оси. Для произвольных вещественных n это невозможно, поэтому степенная функция с вещественным показателем определена только для положительных x .

Показательная функция — математическая функция , где a называется «основанием», а x — «показателем» степени.

• В вещественном случае основание степени  — некоторое неотрицательное вещественное (действительное) число, а аргументом функции является вещественный показатель степени.

• В теории комплексных функций рассматривается более общий случай, когда аргументом и показателем степени может быть произвольное комплексное число.

• В самом общем виде — u^v, введена Лейбницем в 1695 г.

Особо выделяется случай, когда в качестве основания степени выступает число e. Такая функция называется экспонентой (вещественной или комплексной).

Функция y = log_a х (где а > 0, а $$\ne$$1) называется логарифмической.

Построение графиков. График логарифмической функции log_aх можно построить, воспользовавшись тем, что функция log_aх обратна показательной функции y = a^x. Поэтому достаточно построить график функции y = a^x, а затем отобразить его симметртрично относительно прямой у = х.

Свойства функции у = logaх , a > 1: D(f) = (0; +$$\infty$$); не является ни четной, ни нечетной; возрастает на (0; +$$\infty$$); не ограничена сверху, не ограничена снизу; не имеет ни наибольшего, ни наименьшего значений; непрерывна; E(f) = (-$$\infty$$;+ $$\infty$$); выпукла вверх; дифференцируема.	Свойства функции у = logaх , 0 < a < 1 : D(f) = (0;+$$\infty$$ ); не является ни четной, ни нечетной; убывает на (0; +$$\infty$$); не ограничена сверху, не ограничена снизу; нет ни наибольшего, ни наименьшего значений; непрерывна; E(f) = (-;$$\infty$$+ $$\infty$$); выпукла вниз; дифференцируема.
Свойства функции у = ln х : D(f) = (0; +$$\infty$$); не является ни четной, ни нечетной; возрастает на {0; +$$\infty$$); не ограничена сверху, не ограничена снизу; не имеет ни наибольшего, ни наименьшего значений; непрерывна; E(f) = (-$$\infty$$;+ $$\infty$$); выпукла вверх; дифференцируема.

10. Уравнение линии на плоскости. Точка пересечения двух линий. Основные виды уравнений прямой на плоскости (одно из них вывести).

 Определение. Уравнением линии (кривой) на плоскости называется уравнение, к оторому удовлетворяют координаты и каждой точки данной линии и не удовлетворяют координаты любой точки, не лежащей на этой линии.

Если точка передвигается по линии, то ее координаты, изменяясь, удовлетворяют уравнению этой линии. Поэтому координаты  называются текущими координатами.

Любую линию в принципе можно выразить соответствующим уравнением. Однако не всякое уравнение на определяет на плоскости некоторую линию. Например:  определяет только одну точку (0;0);  не определяет никакого множества точек, т.к. левая часть уравнения не может равняться нулю. Чтобы убедится, лежит ли точка на данной линии , надо проверить, удовлетворяют ли координаты этой точки уравнению .

Уравнения линии могут быть самыми различными, однако надо отметить, что не каждое уравнение имеет геометрический образ в виде линии.

Взаимное расположение двух линий

Чтобы определить взаимное расположение 2-х линий, необходимо знать уравнений этих линий. Если система этих уравнений совместна, то линии имеют общие точки. В противном случае общих точек нет. Число общих точек равно числу решений системы уравнений

Например, прямая линия и окружность  имеют 2 общие точки, так как система из этих уравнений имеет два решения:

.

Уравнение прямой на плоскости

В декартовой системе координат рассмотрим прямую , расположенную под углом  к оси (рис. 3.7).

Выберем на прямой L произвольную точку . Из найдем тангенс угла наклона прямой: . Введем угловой коэффициент прямой . Из последнего равенства              (3.1)

Полученное уравнение называется уравнением прямой с угловым коэффициентом.

Уравнение прямой, проходящей через заданную точку в данном направлении

Пусть прямая  образует с осью  угол  и проходит через точку . Т.к. , то ее координаты удовлетворяют уравнению (3.1), т.е. .                               (3.2) Вычитая из (3.1) уравнение (3.2), получим   .                          (3.3)   Полученное уравнение называется уравнением прямой по точке и угловому коэффициенту .

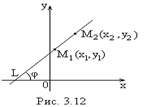
Уравнение прямой, проходящей через две заданные точки

Пусть известны две точки, принадлежащие , . Запишем уравнение прямой по точке  и угловому коэффициенту : .                               (3.4) Т.к. точка  также принадлежит , то ее координаты будут удовлетворять данное равенство: .

Из последнего равенства   . Подставляя выражение для  в  уравнение (3.4):     , получим уравнение прямой по двум точкам

                                                              (3.5).