
- •Вопросы для самопроверки по дисциплине «Математика (Модуль 1)»
- •Чётность
- •Уравнение пучка прямых Уравнение прямой в отрезках
- •Общее уравнение прямой и его исследование
- •Предел числовой последовательности
- •Предел функции в бесконечности и в точке
- •Признаки существования предела
- •Свойства бесконечно малых
- •15.Второй замечательный предел, число е. Понятие о натуральных логарифмах.
- •16. Непрерывность функции в точке и на промежутке. Свойства функций, непрерывных на отрезке. Точки разрыва. Примеры.
- •17. Производная и ее геометрический смысл. Уравнение касательной к плоской кривой в заданной точке.
- •18. Дифференцируемость функций одной переменной. Связь между дифференцируемостью и непрерывностью функции (доказать теорему).
- •19. Основные правила дифференцирования функций одной переменной (одно из этих правил доказать).
- •20. Формулы производных основных элементарных функций (одну из формул вывести). Производная сложной функции.
- •21. Теоремы Ролля и Лагранжа (без доказательства). Геометрическая интерпретация этих теорем.
- •26. Общая схема исследования функций и построения их графиков. Пример.
- •29. Дифференциал функции и его геометрический смысл. Инвариантность формы дифференциала 1-го порядка.
- •30. Понятие первообразной функции. Неопределенный интеграл и его свойства (одно из свойств доказать).
- •31. Метод замены переменной в неопределенном интеграле и особенности применения этого метода при вычислении определенного интеграла.
- •32. Метод интегрирования по частям для случаев неопределенного и определенного интегралов (вывести формулу). Примеры.
- •33. Определенный интеграл как предел интегральной суммы. Свойства определенного интеграла.
- •34. Теорема о производной определенного интеграла по переменному верхнему пределу. Формула Ньютона–Лейбница.
- •34. Несобственные интегралы с бесконечными пределами интегрирования. Интеграл Пуассона (без доказательства).
- •35. Вычисление площадей плоских фигур с помощью определенного интеграла. Примеры.
18. Дифференцируемость функций одной переменной. Связь между дифференцируемостью и непрерывностью функции (доказать теорему).
Функция f(x) называется дифференцируемой
в точке
![]() ,
если её приращение в этой точке
,
если её приращение в этой точке
![]() представимо
в виде
представимо
в виде
![]() ,
где А – некоторая константа.
,
где А – некоторая константа.
![]() ,
где
,
где
![]() .
.
Иначе говоря, функция f дифференцируема
в точке
,
если её приращение есть линейная функция
относительно
![]() с
точностью до бесконечно малых более
высокого порядка, чем
.
с
точностью до бесконечно малых более
высокого порядка, чем
.
Критерий дифференцируемости: пусть
функция f(x) определена в некотором
интервале (а, b) и
![]() ,
тогда функция f(x) дифференцируема в
точке
тогда
и только тогда, когда у неё в точке
существует
производная.
,
тогда функция f(x) дифференцируема в
точке
тогда
и только тогда, когда у неё в точке
существует
производная.
Доказательство:
![]() пусть
функция f дифференцируема в точке
,
тогда её приращение по определению
представимо в виде:
пусть
функция f дифференцируема в точке
,
тогда её приращение по определению
представимо в виде:
![]() .
.
![]() ,
то есть производная существует.
,
то есть производная существует.
![]() Пусть
у функции f(x) в точке
существует
производная, то есть существует конечный
предел
Пусть
у функции f(x) в точке
существует
производная, то есть существует конечный
предел
![]() .
.
![]() .
.
![]() .
.
Теорема доказана.
Следствие: коэффициент А в представлении приращения дифференцируемой функции есть производная функции в точке .
Главная линейная относительно
часть
приращения линейной функции называется
дифференциалом функции в точке
:
![]() .
.
Теорема. Необходимое условие дифференцируемости: если функция дифференцируема в точке ,то она непрерывна в этой точке.
Доказательство: функция дифференцируема
в точке
,
то есть:
![]() .
Покажем, что
.
Покажем, что
![]() .
.
![]() .
.
Если покажем, что
![]() ,
то докажем непрерывность функции.
,
то докажем непрерывность функции.
![]() .
.
![]()
Класс дифференцируемых функций является подмножеством класса непрерывных функций.
Это условие достаточным не является.
Например, функция y=|x|. Эта функция непрерывна в точке х=0, но дифференцируемой в ней не является.
![]() ,
,
![]() .
.
![]() функция
не дифференцируема в точке 0.
функция
не дифференцируема в точке 0.
19. Основные правила дифференцирования функций одной переменной (одно из этих правил доказать).
При
доказательстве правил дифференцирования
будем считать функции f(x)
и g(x)
дифференцируемыми на некотором промежутке
X.
То
есть, для любого
![]() справедливо
справедливо
![]() ,
где
,
где
![]() -
приращения соответствующих функций.
В
другой записи
-
приращения соответствующих функций.
В
другой записи
![]() .
К основным правилам
дифференцирования относят:
.
К основным правилам
дифференцирования относят:
вынесение постоянного множителя за знак производной;
производная суммы, производная разности;
производная произведения функций;
производная частного двух функций (производная дроби).
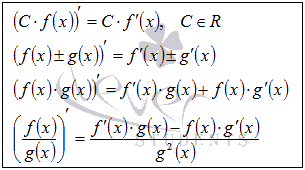
20. Формулы производных основных элементарных функций (одну из формул вывести). Производная сложной функции.
Таблица производных простейших элементарных функций
Легко получить следующую таблицу производных основных элементарных функций, используя определение производной. Для более подробного изучения данного материала рекомендуем использовать, например, "Математический анализ" ч.1 В.А. Ильина, В.А. Садовничего, Бл.Х. Сендова.
(u(x))' = u-1(x)u'(x), в частности,
(1/u(x))'
= -u'(x)/u2(x),
(![]() )'
= u'(x)/2
;
)'
= u'(x)/2
;
(logau(x))' = (u'(x)logae)/u(x) при 0<a1, u(x)>0, в частности, (ln u(x))' = u'(x)/u(x);
(au(x))' = au(x)ln a u'(x) при 0<a1, в частности, (eu(x))' = u'(x)eu(x);
(sin u(x))' = cos u(x)u'(x);
(cos u(x))' = -sin u(x)u'(x);
(tg u(x))' = u'(x)/cos2u(x) x/2+ n, n=0,+-1,...;
(ctg u(x))' = -u'(x)/sin2u(x) x n, n=0,+-1,...;
(arcsin u(x))' = u'(x)/
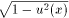 ,
-1<u(x)<1;
,
-1<u(x)<1;
(arccos u(x))' = -u'(x)/ , -1<u(x)<1;
(arctg u(x))' = u'(x)/(1+u2(x));
(arcctg u(x))' = -u'(x)/(1+u2(x)).
Введем гиперболические функции:
sh x = (1/2)(ex-e-x)- гиперболический синус;
ch x = (1/2)(ex+ex)- гиперболический косинус;
th x = sh x/ch x -гиперболический тангенс;
cth x = ch x/sh x - гиперболический котангенс.
Из определения гиперболических функций элементарно вытекают следующие формулы для нахождения их производных.
(sh x)' = ch x;
(ch x)' = sh x;
(th x)' = 1/ch2 x;
(cth x)' = -1/sh2 x.
Пример 7. Найти y', если
y(x) = x3arcsin x.
![]()
y(x) = ln sin (x2+1).
y' = (2xcos(x2+1))/sin(x2+1) = 2x ctg(x2+1)
Замечание. Производная любой элементарной функции является элементарной функцией, то есть операция дифференцирования не выводит из класса элементарных функций.
"Двухслойная" сложная функция записывается в виде
![]()
где u = g(x) - внутренняя функция,
являющаяся, в свою очередь, аргументом
для внешней функции f.
Если f
и g - дифференцируемые функции, то
сложная функция
![]() также
дифференцируема по x и ее производная
равна
также
дифференцируема по x и ее производная
равна
![]()
Данная формула показывает, что производная сложной функции равна произведению производной внешней функции на производную от внутренней функции. Важно, однако, что производная внутренней функции вычисляется в точке x, а производная внешней функции - в точке u = g(x)! Эта формула легко обобщается на случай, когда сложная функция состоит из нескольких "слоев", вложенных иерархически друг в друга.
