
- •Вопросы для самопроверки по дисциплине «Математика (Модуль 1)»
- •Чётность
- •Уравнение пучка прямых Уравнение прямой в отрезках
- •Общее уравнение прямой и его исследование
- •Предел числовой последовательности
- •Предел функции в бесконечности и в точке
- •Признаки существования предела
- •Свойства бесконечно малых
- •15.Второй замечательный предел, число е. Понятие о натуральных логарифмах.
- •16. Непрерывность функции в точке и на промежутке. Свойства функций, непрерывных на отрезке. Точки разрыва. Примеры.
- •17. Производная и ее геометрический смысл. Уравнение касательной к плоской кривой в заданной точке.
- •18. Дифференцируемость функций одной переменной. Связь между дифференцируемостью и непрерывностью функции (доказать теорему).
- •19. Основные правила дифференцирования функций одной переменной (одно из этих правил доказать).
- •20. Формулы производных основных элементарных функций (одну из формул вывести). Производная сложной функции.
- •21. Теоремы Ролля и Лагранжа (без доказательства). Геометрическая интерпретация этих теорем.
- •26. Общая схема исследования функций и построения их графиков. Пример.
- •29. Дифференциал функции и его геометрический смысл. Инвариантность формы дифференциала 1-го порядка.
- •30. Понятие первообразной функции. Неопределенный интеграл и его свойства (одно из свойств доказать).
- •31. Метод замены переменной в неопределенном интеграле и особенности применения этого метода при вычислении определенного интеграла.
- •32. Метод интегрирования по частям для случаев неопределенного и определенного интегралов (вывести формулу). Примеры.
- •33. Определенный интеграл как предел интегральной суммы. Свойства определенного интеграла.
- •34. Теорема о производной определенного интеграла по переменному верхнему пределу. Формула Ньютона–Лейбница.
- •34. Несобственные интегралы с бесконечными пределами интегрирования. Интеграл Пуассона (без доказательства).
- •35. Вычисление площадей плоских фигур с помощью определенного интеграла. Примеры.
Признаки существования предела
Теорема 1. Если числовая последовательность монотонна и ограничена, то она имеет предел.
Теорема
2. Если в некоторой окрестности точки
![]() (или
при достаточно больших значениях
)
функция
(или
при достаточно больших значениях
)
функция
![]() заключена
между двумя функциями
заключена
между двумя функциями
![]() и
и
![]() ,
имеющими одинаковый предел
при
,
имеющими одинаковый предел
при![]() (или
),
то функция
имеет
тот же предел
.
(или
),
то функция
имеет
тот же предел
.
Пусть
при
![]() ,
,
![]() .
.
Это
означает, что для любого
![]() найдется
такое число
найдется
такое число
![]() ,
что для всех
,
что для всех
![]() и
удовлетворяющих условию
и
удовлетворяющих условию
![]() будут
верны одновременно неравенства:
будут
верны одновременно неравенства:
![]() (1.1)
(1.1)
или
![]()
Т.к. по условию функция заключена между двумя функциями, т.е.:
![]() ,
то из неравенств (1.1) следует, что
,
то из неравенств (1.1) следует, что
![]() ,
т.е.:
,
т.е.:
![]() .
.
А это
и означает, что
![]()
13. Определение предела функции в точке. Основные теоремы о пределах (одну из них доказать).
Предел функции в точке: Пусть функция задана в некоторой окрестности точки , кроме, быть может, самой точки .
Определение.
Число
называется
пределом функции
![]() при
стремящемся
к
(или
в точке
),
если для любого, даже сколько угодно
малого положительного числа
,
найдется такое положительное число
при
стремящемся
к
(или
в точке
),
если для любого, даже сколько угодно
малого положительного числа
,
найдется такое положительное число
![]() (зависящее
от
),
что для всех
,
не равных
и
удовлетворяющих условию
,
выполняется неравенство
(зависящее
от
),
что для всех
,
не равных
и
удовлетворяющих условию
,
выполняется неравенство
![]() .
.
Это
предел функции обозначается:
![]() или
при
или
при
![]() .
.
Если
при стремлении
к
переменная
принимает
лишь значения, меньшие
,
или наоборот, лишь значения большие
,
и при этом функция
стремится
к некоторому числу
,
то говорят об односторонних пределах
функции
соответственно
слева
![]() и
справа
и
справа
![]()
1. Предел константы равен самой этой константе:
![]() с
= с.
с
= с.
2. Постоянный множитель можно выносить за знак предела:
[ k • f (х)] = k • f (х).
3. Предел суммы (разности) функций равен сумме (разности) пределов этих функций:
[ f (х) ± g (х)] = f (х) ± g (x).
4. Предел произведения функций равен произведению пределов этих функций:
[ f (х) • g (х)] = f (х) • g (x).
5. Предел отношения двух функций равен отношению пределов этих функций, если только предел делителя не равен нулю:
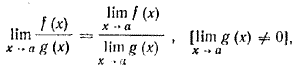
14. Бесконечно малые величины (определение). Свойства бесконечно малых (одно из них доказать). Бесконечно большие величины, их связь с бесконечно малыми.
Бесконечно малая (величина) — числовая функция или последовательность, которая стремится к нулю.
Бесконечно большая (величина) — числовая функция или последовательность, которая стремится к бесконечности определённого знака.
Свойства бесконечно малых
Сумма конечного числа бесконечно малых — бесконечно малая.
Произведение бесконечно малых — бесконечно малая.
Произведение бесконечно малой последовательности на ограниченную — бесконечно малая. Как следствие, произведение бесконечно малой на константу — бесконечно малая.
Если an — бесконечно малая последовательность, сохраняющая знак, то
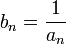 — бесконечно
большая последовательность.
— бесконечно
большая последовательность.
Связь бесконечно больших и бесконечно малых величин устанавливает следующая теорема.
Теорема
2.16
Пусть
![]() --
функция, бесконечно большая при базе
--
функция, бесконечно большая при базе
![]() .
Тогда величина
.
Тогда величина
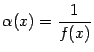 --
бесконечно малая при базе
.
--
бесконечно малая при базе
.
Доказательство.
Для начала заметим, что на всех достаточно
далёких окончаниях
![]() базы
будет
базы
будет
![]() ,
так что функция
,
так что функция
![]() определена
на этих окончаниях. Далее, пусть взято
некоторое
определена
на этих окончаниях. Далее, пусть взято
некоторое
![]() .
Положим
.
Положим
 и
выберем такое окончание
,
что
и
выберем такое окончание
,
что
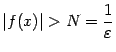 при
при
![]() из
этого окончания. Тогда
из
этого окончания. Тогда
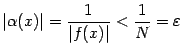 при
таких
,
что и означает, что
при
таких
,
что и означает, что
![]() .
.
Замечание
2.9
Утверждение, обратное к доказанной
теореме, вообще говоря, неверно: если
--
бесконечно малая при базе
,
то функция
 не
всегда является бесконечно большой при
базе
,
хотя бы потому, что может быть не
определена ни на каком окончании
базы
.
Простейший пример -- это постоянная
величина
не
всегда является бесконечно большой при
базе
,
хотя бы потому, что может быть не
определена ни на каком окончании
базы
.
Простейший пример -- это постоянная
величина
![]() ,
которая, очевидно, бесконечно мала при
любой базе (
,
которая, очевидно, бесконечно мала при
любой базе (
![]() ),
но
),
но
![]() не
имеет смысла ни при каких
.
Однако если сделать дополнительное
предположение, что
не
имеет смысла ни при каких
.
Однако если сделать дополнительное
предположение, что
![]() при
всех
из
некоторого окончания
базы
,
то обратное утверждение становится
верным.
при
всех
из
некоторого окончания
базы
,
то обратное утверждение становится
верным.
