
- •4)Бб и бм последовательности
- •5)Предел ф-ции, арифметика пределов. Критерий Коши
- •9) Свойства непрерывных функций (теорема о максимуме)
- •11) Производные от элементарных функций, от сложной и обратной функции, от функции заданных параметрически.
- •12) Дифференциал, его геометрический смыл. Инвариантность дифференциала. Применение дифференциала в численных задачах.
- •19)Выпуклость ф-ции и знак второй производной. Точки перегиба
- •20)Необходимое и достаточное условия максимума (минимума) функции одной переменной
- •21)Схема решения задач на глобальный и локальный минимум
- •22)Асимптоты ф-ции
- •23)Общий план построения графиков и исследования ф-ций.
- •24)Первообразная. Определение и основные свойства первообразной. Таблица основных первообразных
- •25)Замена переменной интегрирование по частям в первообразной
- •26)Полиномы, рациональные ф-ции , разложение рациональной ф-ции на простейшие рациональные ф-ции.
- •28)Интегралы от выражений с радикалами. Подстановки Эйлера
- •29)Интегрирование тригонометрических ф-ций
- •30)Определенный интеграл. Определение основные св-ва
- •31) Интеграл как функция верхнего предела. Непрерывность. Формула Ньютона-Лейбница.
- •32) Замена переменной и интегрирование по частям в определенном интеграле.
- •33) Несобственные интегралы первого рода
- •34) Несобственные интегралы второго рода
- •36)Объем и площадь боковой поверхности тел вращения
32) Замена переменной и интегрирование по частям в определенном интеграле.
 - формула замены
переменной в определенном интеграле.
Когда мы меняем переменные мы делаем
3 изменения переменной у f
аргумента умнож. подынтегральное
выражение
- формула замены
переменной в определенном интеграле.
Когда мы меняем переменные мы делаем
3 изменения переменной у f
аргумента умнож. подынтегральное
выражение
 ,
меняется предел интеграла. В определенном
интеграле нет необходимости возвращаться
к исходному перемещению.
,
меняется предел интеграла. В определенном
интеграле нет необходимости возвращаться
к исходному перемещению.
33) Несобственные интегралы первого рода
Пусть
f(x)
определена и непрерывна на множестве
от [a,+∞)
и
 .
Тогда:
.
Тогда:
Если
 ,
то используется обозначение I=
,
то используется обозначение I= и
интеграл называется несобственным
интегралом Римана первого рода.
В этом случае называется сходящимся.
и
интеграл называется несобственным
интегралом Римана первого рода.
В этом случае называется сходящимся.
Если
не существует конечного
 (
( ),
то интеграл
называется расходящимся к «∞» , «
),
то интеграл
называется расходящимся к «∞» , « ∞»,
или просто расходящимся.
∞»,
или просто расходящимся.
Пусть
f(x)
определена и непрерывна на множестве
от (-∞,b]
и
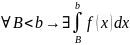 . Тогда:
. Тогда:
Если
 , то используется обозначение I=
, то используется обозначение I=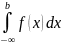 и интеграл называется несобственным
интегралом Римана первого рода.
В этом случае I=
называется
сходящимся.
и интеграл называется несобственным
интегралом Римана первого рода.
В этом случае I=
называется
сходящимся.
Если
не существует конечного
 (
( ∄),
то интеграл
называется
расходящимся к «∞», «
∞»,
или просто расходящимся.
∄),
то интеграл
называется
расходящимся к «∞», «
∞»,
или просто расходящимся.
Если
функция f(x)
определена и непрерывна на всей числовой
прямой, то может существовать несобственный
интеграл данной функции с двумя
бесконечными пределами интегрирования,
определяющийся формулой: =
= =
= ,
где с — произвольное число.
,
где с — произвольное число.
34) Несобственные интегралы второго рода
Пусть
f(x)
определена на (a,b],
терпит бесконечный разрыв в точке x=a и
 . Тогда:
. Тогда:
Если
 ,
то используется обозначение I=
,
то используется обозначение I= и интеграл называется несобственным
интегралом Римана второго рода.
В этом случае интеграл называется
сходящимся.
и интеграл называется несобственным
интегралом Римана второго рода.
В этом случае интеграл называется
сходящимся.
Если
 (
∄),
то обозначение сохраняется, а I=
называется расходящимся к «∞», «
∞»,
или просто расходящимся.
(
∄),
то обозначение сохраняется, а I=
называется расходящимся к «∞», «
∞»,
или просто расходящимся.
Пусть
f(x)
определена на [a,b)
, терпит бесконечный разрыв при x=b и
 . Тогда:
. Тогда:
Если
 , то используется обозначение I=
и интеграл называется несобственным
интегралом Римана второго рода.
В этом случае интеграл называется
сходящимся.
, то используется обозначение I=
и интеграл называется несобственным
интегралом Римана второго рода.
В этом случае интеграл называется
сходящимся.
Если
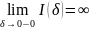 (
∄),
то обозначение сохраняется, а I=
называется
расходящимся к «∞», «
∞»,
или просто расходящимся.
(
∄),
то обозначение сохраняется, а I=
называется
расходящимся к «∞», «
∞»,
или просто расходящимся.
Если
функция f(x)
терпит разрыв во внутренней точке c
отрезка [a;b],
то несобственный интеграл второго рода
определяется формулой:
= =
=
35)
Длина кривой и площадь плоской фигуры.
Заменяем малый сектор на треугольник.
∆SK=1/2
r
(φk)r(φk-∆φk)*sin∆φk=1/2
r2(φk)
∆φk
δ= S=
S=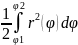
Длина.
∆lk=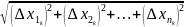 L=
L=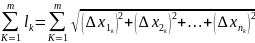 ∆tk=tk+1+tk
L=
∆tk=tk+1+tk
L=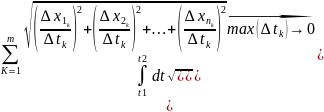
36)Объем и площадь боковой поверхности тел вращения
Рассмотрим
тело образованное вращением вокруг Ox
криволинейной трапеции аАВb
ограниченной кривой y=f(x)осью
Ох и прямыми х=а и х=b
в этом случае произвольное сечение
тела плоскостью ,перпендикулярной к
оси абсцисс ,есть круг площадь которого
 применяя общую формулу для вычисления
объема получим ф-лу для вычисления
объема тела вращения
применяя общую формулу для вычисления
объема получим ф-лу для вычисления
объема тела вращения

36)
Площадь

 =
= =∆xk
=∆xk
 ∆xk
∆xk
 S=
S=
