24)Первообразная. Определение и основные свойства первообразной. Таблица основных первообразных
О:
ф-ция G(x)
называется первообразной если выполняется
равенство:
Свойства первообразной.
Перечислим свойства первообразной.
1. Если F– первообразная для ф-ции f, то F + С, где С – константа, тоже
2. Если F1 и F2 – две первообразные для одной и той же функции f, то они отличаются на постоянное слагаемое.
3.пусть F и G – первообразные для функций f и g соответственно. Тогда F + G является первообразной для функции f + g: (F + G)' = F' + G' =f + g.
4.константа выносится за знак первообразной
25)Замена переменной интегрирование по частям в первообразной
Замена переменной
пусть
требуется найти интеграл
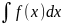сделаем замену переменной
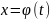где
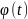непрерывная
ф—ция с непрерывной производной имеющая
обратную ф-цию. Тогда
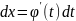;докажем
что в этом случае имеет место нер-во:
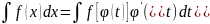(после интегрирования
в правой части равенства вместо t
будет подставлено его выражение через
х )нужно
доказать что производные обеих частей
по х равны. Находим производную от левой
части
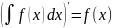Дифференцируем правую часть
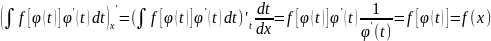
Следовательно части равны читд.
Интегрирование по частям
Пусть
u
и v
–две дифференцируемые ф-ции от х . тогда
как известно дифференциал произведения
вычисл.по ф-ле: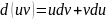
Отсюда интегрируя получаем
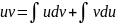или
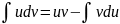- ф-ла интегрирования
по частям
26)Полиномы, рациональные ф-ции , разложение рациональной ф-ции на простейшие рациональные ф-ции.
Функция 
называется рациональной
функцией,
или рациональной
дробью,
если она представляет собой отношение
двух многочленов 
и 
:
Пусть
степень многочлена
равна 
,
а степень
равна 
,
то есть
Q(x)= тому же только а на б замени.
где 
и 
Т(теорема Безу): При делении многочлена f(x)на разность x-a получается остаток, равный f(a).
Т(основная теорема алгебры): Всякая целая рац ф-ция f(x)имеет по крайней мере один корень, действительный или комплексный
27)Интегралы
от рациональных ф-ций Для
интегрирования рациональной функции 
,
где P(x) и Q(x) -
полиномы, используется следующая
последовательность шагов:
Если дробь неправильная (т.е. степень P(x) больше степени Q(x)), преобразовать ее в правильную, выделив целое выражение;
Разложить знаменатель Q(x) на произведение одночленов и/или несократимых квадратичных выражений;
Разложить рациональную дробь на простейшие дроби, используя метод неопределенных коэффициентов;
Вычислить интегралы от простейших дробей.
28)Интегралы от выражений с радикалами. Подстановки Эйлера
Рассмотрим
интеграл
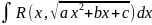где а≠0
1.Первая
подстановка эйлера если а>0 то полагаем
=
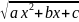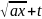перед корнем
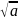возьмем для определенности знак плюс
тогда
откуда
х опред рациональная ф-ция от t
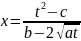следовательно
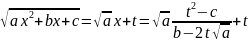т.е.
оказывается рациональной функцией от
t,так
как x,dx
и
выражаются через t,
значит
данный интеграл преобразуется в интеграл
от рациональной ф-ции от t.
2.Вторая
подстановка Эйлера если с>0 то полагаем
=xt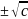
тогда перед
для определенности знак плюс
=
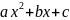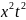+2xt
+c
Отсюда
х опред как рац ф-ция от t
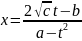т.к. dx
и
тоже выражаются рационально через t то
подставляя значения x,
и dx
в интеграл
мы сведем его к интегралу от рац. Ф-ции
от t
3.Третья подстановка эйлера .Пусть а и b действительные корни трехчлена . Полагаем =(x-a)t
Так
как
,
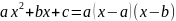то
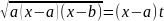
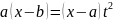отсюда находим х
как рац ф-цию от t
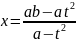так
как . dx
и
тоже рационально зависят от t
то данный интеграл преобраз. В интеграл
от рац. Ф-ции от t