4.3. Класичні ітераційні методи

Було показано, що коли рівняння має корінь , а функція не змінює знак у деякому околі , то рівняння

(4.10)

також має корінь - . При цьому функцію вибирають такою, щоб ітераційний процес для рівняння (4.10) був збіжним. У одному з випадків методу простої ітерації як ми обирали сталу .

Розглянемо два класичних методи, які можливо одержати іншим вибором функції .

4.4. Метод січних (хорд, лінійної інтерполяції)

Нехай - дійсна функція дійсної змінної , а - дійсний корінь рівняння . Припустимо, що у деякому околі точки функція , а та у цьому околі не змінюють знак. Це означає, що при переході через функція змінює знак та має точку простим коренем. Нехай - точка цього околу, в якій . У виразі (4.1) як функцію візьмемо функцію

.

Тоді рівняння

(4.11)

також має корінь .

За початкове наближення візьмемо довільну, достатньо наближену до точку цього околу, в якій має знак, протилежний знаку , а наступні наближення будуємо звичайним способом:

. (4.12)

Далі у викладках враховуємо, що . Тому що, з одного боку,

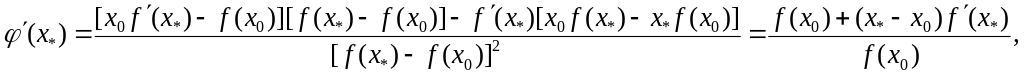а, з іншого боку, за формулою Тейлора^

де міститься проміж та . То якщо покласти , одержуємо

Отже,

,

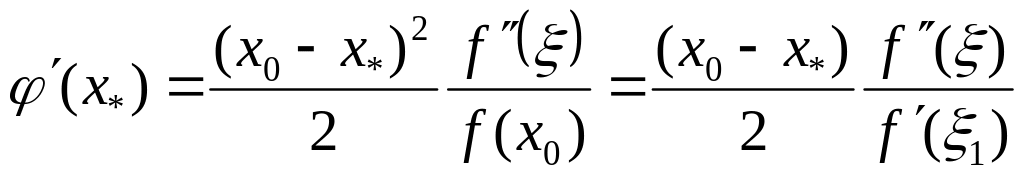тому що

При , достатньо близькому до , - незначна величина, і тому існує такий окіл .

Якщо взяти з цього околу, то послідовність (3) буде збігатися до .

Оскільки , то позначивши , будемо мати , що дає змогу на кожному кроці по значенням стежити за досягнутою точністю.

Геометрично цей метод полягає у тому, що значення є абсцисою точки перетину прямої, що проходить через точки та , з віссю (див. рис. 6, 7, 8 ,9).

Рис. 6 Рис. 7

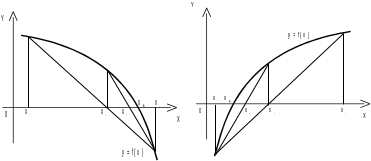(f ^/(x)<0 , f ^//(x)<0) (f ^/(x)>0 , f ^//(x)<0)

Рис. 8 Рис. 9

Тому цей метод називають методом січних (хорд).

4.5. Метод Ньютона (метод дотичних)

Другий класичний метод розв’язання рівняння - метод Ньютона, одержуємо, якщо покладемо в (4.1)

,

тобто зведемо задачу відшукання кореня рівняння до пошуку кореня рівняння

. (4.13)

Припустимо, що на відрізку , де знаходиться єдиний корінь рівняння , функція має неперервні похідні та , що не перетворюються у нуль на цьому відрізку.

У цьому разі

та .

Це означає, що існує такий окіл точки , що коли початкове наближення узято з цього околу, то послідовність

, (4.14)

буде збігатися до . Початкове наближення доцільно обирати так, щоб було

. (4.15)

Метод Ньютона може бути застосовано не тільки для відшукання дійсних коренів рівняння , але й комплексних коренів, тільки слід мати на увазі, що при відшуканні комплексного кореня у разі дійсної функції початкове наближення необхідно брати комплексним числом, а не дійсним.

У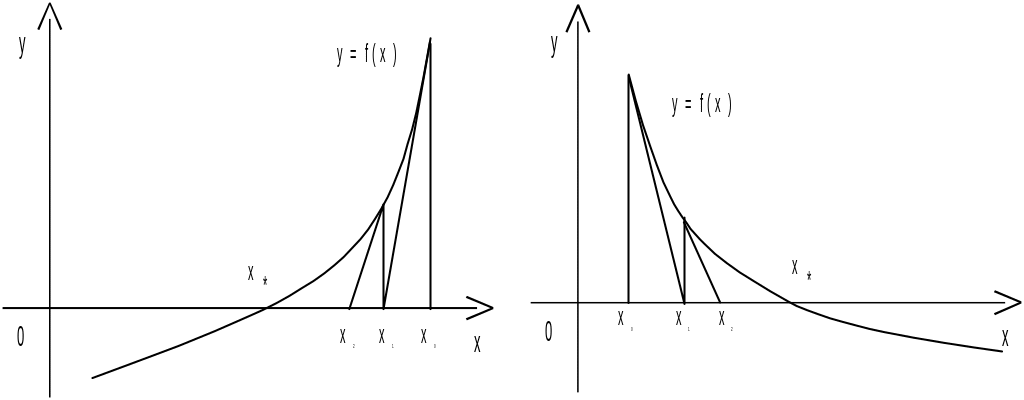 разі, коли є дійсним коренем рівняння , цей метод має просту геометричну інтерпретацію. Значення є абсцисою точки перетину дотичної до кривої у точці з віссю . Тому метод Ньютона часто називають методом дотичних. Як бачимо з рис. 10, 11, 12, 13, послідовні наближення до дійсного кореня у методі Ньютона збігаються до нього монотонно, наближуючись з боку .

(f ^/(x)>0 , f ^//(x)>0) (f ^/(x)<0 , f ^//(x)>0)

Рис. 10 Рис. 11

Р

(f ^/(x)>0 , f ^//(x)<0) (f ^/(x)<0 , f ^//(x)<0)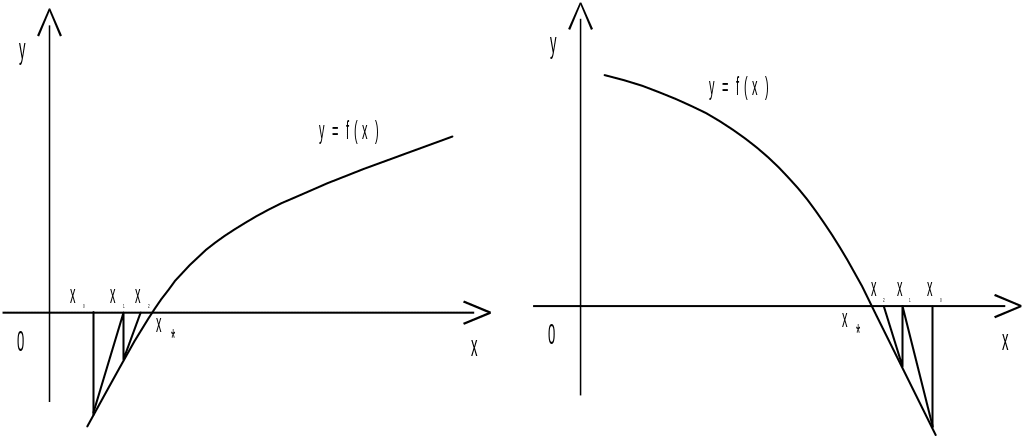

ис. 12 Рис. 13

Коли за початкове наближення у методі Ньютона взяти точку , де , то, як бачимо з рисунка, можна не дійти до кореня , якщо тільки початкове наближення не дуже добре.

Швидкість збіжності методу Ньютона можна визначити так.

За формулою Тейлора

.

Тоді

.

Отже,

.

Якщо , де - відрізок, що містить та , на якому не змінює знак і , то

.

Це свідчить про швидку збіжність методу Ньютона.