4.6. Комбінований метод

Комбінуючи метод січних і метод Ньютона, можна одержати метод відшукання дійсних коренів рівняння , перевага якого полягає у тому, що при попередніх припущеннях відносно і послідовні наближення і знаходяться по різні боки від кореня, і тому можна стежити у процесі обчислень за одержаною точністю, до того ж він збігається значно швидше методу січних.

Нехай на відрізку міститься єдиний корінь рівняння , а та на цьому відрізку не змінюють знаки.

Якщо (рис. 14, 15), то знаходимо і за формулами

, (4.16)

а наступні наближення знаходимо за формулами

. (4.17)

(f (a) f ^//(a)>0) (f (a) f ^//(a)>0)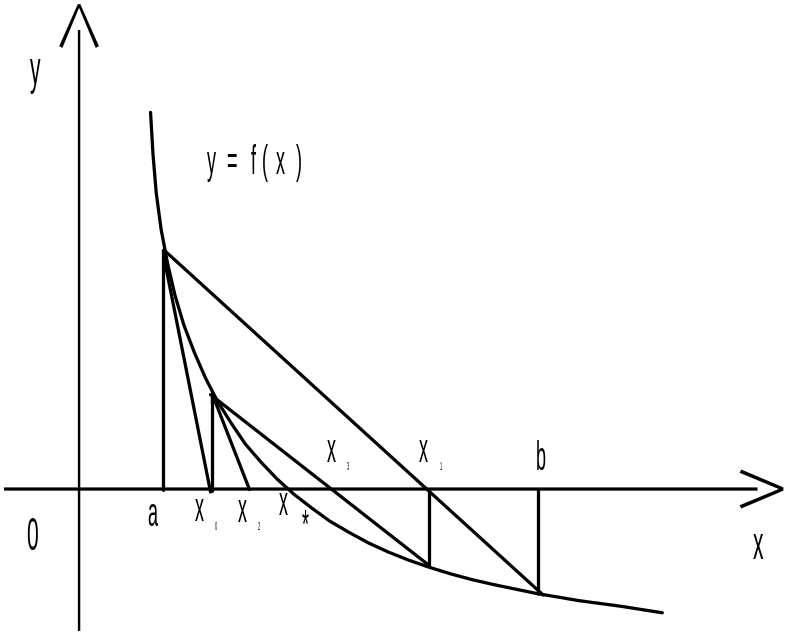

Рис. 14 Рис.15

Коли ж (рис. 16, 17), то і знаходимо за формулами

(4.16′)

а наступні наближення – за формулами (4.17).

(f (b) f ^//(b)>0) (f (b) f ^//(b)>0)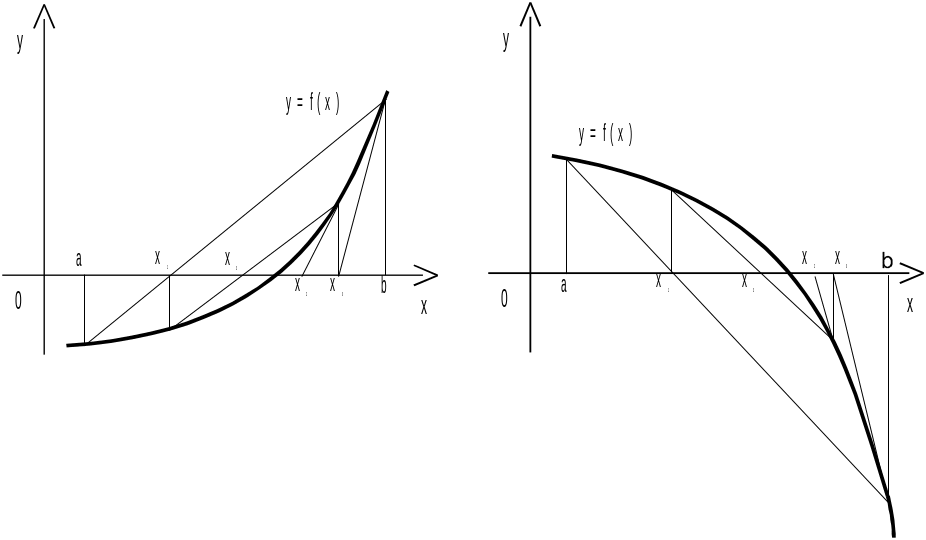

Рис. 16 Рис. 17

Як бачимо з рисунків, послідовні наближення завжди містяться по різні боки від , та перші знаки і , що збігаються, є вірними знаками для .

4.7. Розв’язання алгебраїчних рівнянь

Означення. Рівняння вигляду

(х)=а₀хⁿ+a₁x^n-1+a₂x^n-2+…+a_n-1x+a_n=0, (4.18)

де а_і, і=0,1,2,…,n - дійсні або комплексні числа, х- невідоме, зветься алгебраїчним рівнянням. Якщо а₀0, то n називають степеню рівняння, числа а_і, і=0,1,2,…,n називаються коефіцієнтами рівняння.

З курсу алгебри відомо, що рівняння (4.18) при а₀0 має точно n коренів(комплексних або дійсних). Для розв’язання рівняння (4.18), взагалі, можливо використовувати ті ж самі методи, які розглянуто вище для нелінійних рівнянь загального виду (наприклад, метод Ньютона).

Для відшукання меж області, у якій містяться всі корені рівняння (4.18), можуть бути корисними такі результати (доведення яких наведено у спецкурсі).

Нехай а₀0, а_n0 і

а=maxa₁,a₂,…,a_n , a’= maxa₀,a₁,…,a_n-1 .

Теорема 1. Усі корені рівняння (4.18) (комплексні та дійсні) містяться у кільці

|a_n|/(a’+|a_n|)  |x|  1+a/|a₀|. (4.19)

Припустимо тепер, що всі коефіцієнти рівняння (4.18) дійсні числа та а₀>0. Будемо цікавитися межами дійсних коренів цього рівняння. Очевидно, достатньо мати способи визначення меж додатних коренів, оскільки замінюючи х на -у ми одержимо рівняння, корені якого відрізняються від коренів вихідного рівняння знаком.

Теорема 2 (Лагранжа). Позначимо через максимум абсолютних величин від’ємних коефіцієнтів рівняння, та нехай перший від’ємний коефіцієнт у послідовності а₀,а₁,…,а_n  а_m. Тоді всі додатні корені (4.18) менше за 1+ . Якщо від’ємних коефіцієнтів немає, то нема і додатних коренів.

4.8. Відшукання коренів алгебраїчних рівнянь методом вилучення множників

Розглянемо спеціалізовані методи розв’язання алгебраїчних рівнянь вищих ступенів.

Відомо, що багаточлен

(х)= а₀хⁿ+a₁x^n-1+…+a_n-1x+a_n (4.20)

з дійсними коефіцієнтами може бути зображений у вигляді добутку багаточленів степеню не вище двох також з дійсними коефіцієнтами.

Лінійні множники у такому зображенні відповідають дійсним кореням рівняння (4.18), а квадратичні - парам комлексно-спряжених коренів. Отже, якщо мати способи розкладання багаточлена на множники, то задача відшукання коренів рівняння (4.18) зводиться до розв’язання зовсім простих рівнянь. У зв’язку з цим розроблені методи вилучення дійсних множників (х).

При застосуванні методів вилучення множників доводиться багато разів виконувати ділення багаточлена на багаточлен, тобто знаходити частку та остачу.

Якщо дільник має першу ступінь, тоді це зручно виконувати за схемою Горнера^* . Нехай потрібно відшукати частку і остачу від ділення багаточлена (4.20) на багаточлен х-r. Позначимо остачу від ділення через R, а часткою нехай буде багаточлен

g(x)=b₀x^n-1+b₁x^n-2+…+b_n-2x+b_n-1.

Тоді R і b_i знаходиться за схемою Горнера

a₀ a₁ a₂ a₃ … a_n-1 a_n |r

+ b₀r b₁r b₂r … b_n-2r b_n-1r

________________________________________

b₀ b₁ b₂ b₃ … b_n-1 R,

де b₀=a₀, а кожне наступне число нижнього рядка дорівнює сумі двох чисел, що знаходяться над ним.

Оскільки R=(r) , тоді схему Горнера можна застосувати і для відшукання значень багаточлена х=r.

Для відшукання частки

g(x)=b₀x^n-2+b₁x^n-3+…+b_n-3x+b_n-2

і остачі

R(x)=c₀x+c₁

від ділення багаточлена (4.20) на х²+рх+q можна використовувати таку схему

| a₀ a₁ a₂ a₃ … a_n-2 a_n-1 a_n

-p | -pb₀ -pb₁ -pb₂ … -pb_n-3 -pb_n-2

-q | -qb₀ -qb₁ … -qb_n-4 -qb_n-3 -qb_n-2

_{_}____|_________________________________________

b₀ b₁ b₂ b₃ … b_n-2 c₀ c₁,

де останній рядок одержується як сума перших трьох рядків.