
- •1. Модель динамики об-в рег-ния уровня в-ва.
- •2. Модель дин-ки об-та рег-ния расхода в-ва.
- •3. Модель дин-ки об-тов рег-ния конц-ции в-в.
- •4. Модель идеал-го перемешивания.
- •5. Модель идеального вытеснения.
- •6. Диффузионные модели (дм).
- •7. Ячеечные модели.
- •8. Моделир-е проц-в прямот-х теплообмен-в без учета тепл-й емкости стенки турбы.
- •9. Моделир-е проц-в противоточ-х теплооб-в без учета тепл-й емкости стенки трубы
- •10. Моделир-е проц-в в теплообмен-х с учетом накопл-я теплоты в его стенках.
- •11. Получ-е перед-х ф-ций для противот-х -в.
- •12. Вывод передат-х ф-ций конденсатора без учета накопл-я тепла в стенке.
- •13. Вывод перед-х ф-ций конденсатора с учетом накопл-я тепла в стенке.
- •15. Оценка взаимосвязи перемен-х статист-й модели на основе кор-го анализа.
- •Определение вида уравнения регрессии.
- •Определение силы линейной связи между , .
- •Определение коэффициентов уравнения регрессии:
- •17. Оценка значимости коэф-в ур-я регрессии. 18. Оценка адекват-сти ур-я регрессии.
- •19. Ортогон-е планы 1-го порядка.
- •Полный факторный эксперимент (пфэ).
- •20. Планы 2-го порядка.
- •Ортогональный план второго порядка.
- •22. Идент-я пар-в перед-й ф-ции м-дом м-нтов.
- •23. Идент-ция пар-в передат-й ф-ции м-дом модулирующих ф-ций.
- •24. Беспоиск-е алг-мы идентиф-и с адапт-й моделью в прост-ве перем-х сост-я.
- •25. Поисковые алгоритмы идент-ции с адаптивной моделью.
- •26. Идентиф-я пар-в перед-й ф-ции м-дом площадей.
- •27. Провед-е экспер-та по снятию перех-х ф-ций. М-ды сглажив-я перех-х ф-ций.
- •28. Виды акт-х возд-й для опред-я динамич-х х-к. Изуч-е объекта и подготовка ап-ры для провед-я эксп-нта.
- •Блочный пр-п разработки мат-х моделей хтп.
- •Основные подходы получения мат-х моделей хтп.
- •30. Матем-я модель проц-а газ-й абсорбщии.
22. Идент-я пар-в перед-й ф-ции м-дом м-нтов.
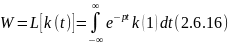
Разложим
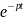 в ряд Падэ:
в ряд Падэ:
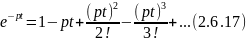
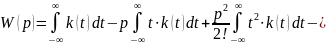

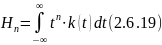
где
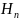 — момент -ого порядка импульсной функции.
— момент -ого порядка импульсной функции.

М-т импульсной функции можно опр-ть по м-нтам кор-й и взаимокорреляционной функции следующим образом:
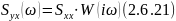
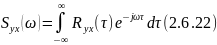
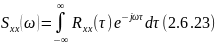
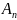 — момент
взаимокорреляционной функции:
— момент
взаимокорреляционной функции:
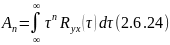
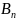 — момент
корреляционной функции
— момент
корреляционной функции
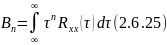
Подставим в 2.6.21; 2.6.22, 2.6.23, 2.6.20:
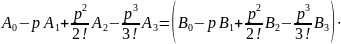

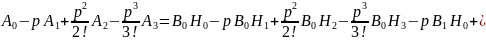
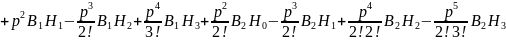
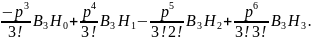
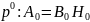 ;
;
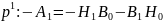 ;
;
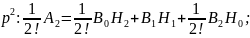
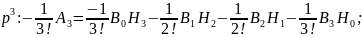
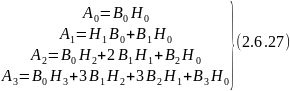
Так как кор-ная ф-ция четная, то все м-нты нечетного порядка будут равны 0. С учетом этого условия перепишем 2.6.27:
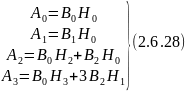
Так
как
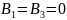 .
.
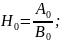
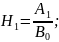
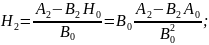

Если
на входе системы действует СП в виде
белого шума, то кор-ная функция опр-ся
в виде -функции, то есть
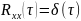 .
Можно подобрать
таким образом, что
.
Можно подобрать
таким образом, что
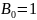 ,
а
,
а
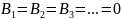 .
Поэтому система 2.6.28 примет вид:
.
Поэтому система 2.6.28 примет вид:
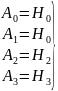 тогда:
тогда:

23. Идент-ция пар-в передат-й ф-ции м-дом модулирующих ф-ций.
Данная задача решается в несколько этапов:
На первом этапе прин-ся и выбирается ДУ -ого прядка, описывающее динамические свойства моделируемого объекта.
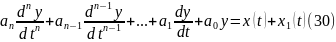
где
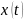 — входная переменная процесса;
— входная переменная процесса;
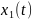 — шум.
— шум.
Принимается, что СП с мат-м ожиданием равным нолю.
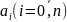 — искомые
коэффициенты.
— искомые
коэффициенты.
На
2м этапе выбир-ся моделирующая ф-ции
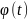 .
Св-ва
:
.
Св-ва
:
она должна быть непрерывной;
она должна быть ограничена и дифференцируема;
на границе интервала
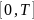 сама функция и все её производные должны
быть равны нолю.
сама функция и все её производные должны
быть равны нолю.
Третий этап. Умножаем уравнение 30 на :
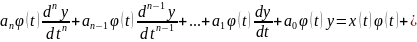
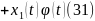
Для нахождения коэффициентов уравнения 31 проинтегрируем его по частям. При этом каждая составляющая интегрируется только раз каков порядок производной этой составляющей. В результате получим;
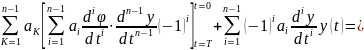
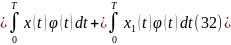
С учетом свойства модулирующих функций:
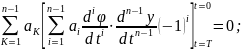
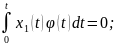
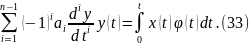
Для
составления
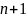 уравнений необходимо составить реализацию
и
уравнений необходимо составить реализацию
и

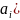 )
)
24. Беспоиск-е алг-мы идентиф-и с адапт-й моделью в прост-ве перем-х сост-я.
Данные алгоритмы идентификации основаны на функц-нии в реальном масштабе времени. Разл-т 2 вида БАИАМ: 1) Общая стр-ра БАИАМ в пр-ве сигналов; 2) БАИАМ с операторной моделью с непрерывными и дискретными временами.
Общая стр-ра БАИАМ в пр-ве сигналов. Идентифицируемый объект описывается в форме 3. Однако с учетом параметрической постановки задачи и наличия шумов оператор объекта может быть записан в следующем виде:
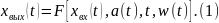
Вектор
параметров
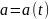 считается в общем случае известным.
Статическая характеристика
считается в общем случае известным.
Статическая характеристика
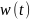 может быть известна и неизвестна.
может быть известна и неизвестна.
Если
идентификация объекта осуществляется
в классе детерминированных моделей с
точностью до вектора параметров
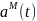 ,
то настраиваемая модель имеет вид:
,
то настраиваемая модель имеет вид:
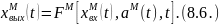 где
— вектор рисковых параметров.
где
— вектор рисковых параметров.
Экспериментальные векторы входных переменных одинаковы:
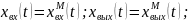
 .
.
Задача
БАИАМ заключается в том, чтобы на основе
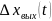 ,
,
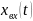 ,
,
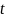 определить вектор параметров модели
по следующему алгоритму:
определить вектор параметров модели
по следующему алгоритму:
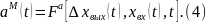
при этом алгоритме величина д.б. минимальной.
Выр-е 4 явл-ся операторной формой алгоритма поиска модели.
Структурная схема алгоритма БАИАМ имеет вид:
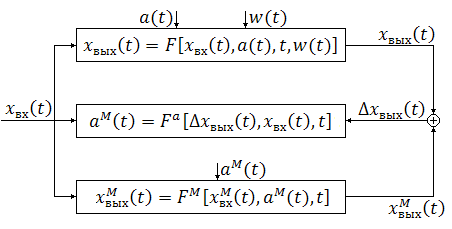
Из
Рис видно, что при малом знач-и в-ны
невязки дан-й БАИАМ не гар-т идент-и в
смысле точного отслеж-я неизвестных
параметров объекта. Это имеет место,
если операторы
и
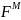 не одинаковы, а также, если в объекте
имеется наличие шума.
не одинаковы, а также, если в объекте
имеется наличие шума.
Отсюда
следует, что данный БАИАМ обесп-т только
малое знач-е в-ны невязки на всем мн-ве
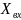 реализации вх-го сигнала
.
Однако для один-х, близких опер-ров
,
это означает приближ-е
реализации вх-го сигнала
.
Однако для один-х, близких опер-ров
,
это означает приближ-е
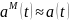 ,
то есть парам-скую идентификацию.
,
то есть парам-скую идентификацию.
2.
Общая стр-ра БАИАМ с дискр-м временем и
операторным описанием.
В данном случае объект опис-ся оператором
1. Однако вх-е и вых-е сигналы квантуются
во времени. На структ-й схеме алгоритма
квант-я можно изобразить с пом-ю преобр-ля
 .
.
Структурная схема БАИАМ с дискретным временем и операторным описанием имеет вид:
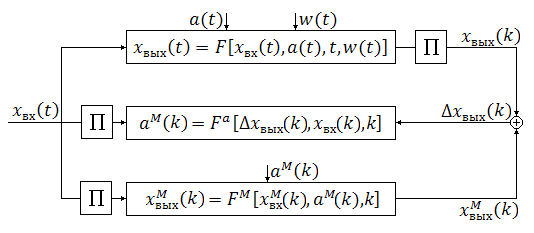
В
качестве
![]() может быть использован АЦП (квантователь
во времени в случае большой разрядности).
может быть использован АЦП (квантователь
во времени в случае большой разрядности).

При этом алгоритм настройки, который реализует данный БАИАМ, имеет следующий вид:
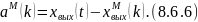
при котором настраиваемая модель имеет операторное описание при операторном описании идентифицируемого объекта (Рис.).

Структура ПАИАМ с дискретным временем и операторным описанием (см. предпоследний Рис. с учетом части структуры, обведенной пунктирной линией на последнем Рис.).
В
данных структурах блоки “вычисление
целевой функции”, “формирование
процесса настойки”, ”алгоритм поиска”
не раскрываются, так как они могут быть
разными для ПАИМ. Алгоритм настройки
должен обеспечивать
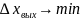 .
.
