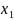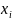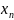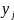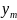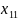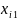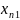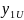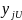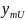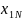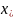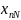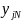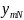11. Получ-е перед-х ф-ций для противот-х -в.

Математическая модель:

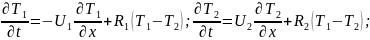
Преобразуем по Лапласу по времени при нулевых начальных условиях (1) и (2):

Преобразуем (6):

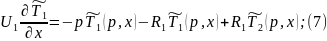
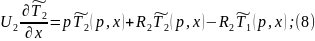
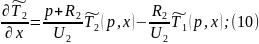
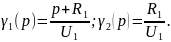
Для решения данной системы уравнений составим матрицу:

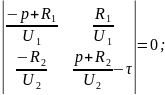
где 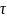— корни матрицы.

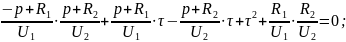
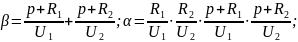
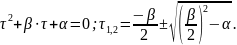
Решение уравнений (7) и (8) с учетом (12) примет следующий вид:

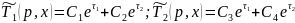
где , , 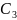, 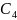— постоянные интегр-я, которые находятся из граничных условий.

Продифференцируем по уравнение (13):

: :

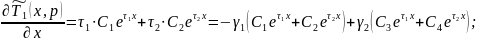
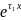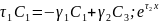Получим граничное условие для 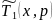из уравнения (13):

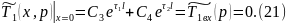
Из (20) определим :

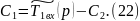
Подставляем (22) в (18):

Из выражения (21) найдем :

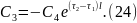
Подставляя (24) в (23):

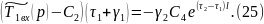
Умножаем левую и правую часть (25) на :

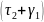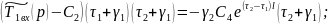
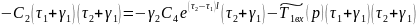
Выражение (19) домножим на :

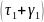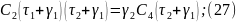
Так как левые части уравнений (26) и (27) равны, то равны их правые части:

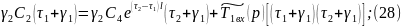
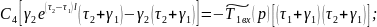
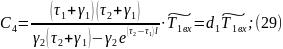
Подставляем (29) в (24):

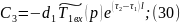
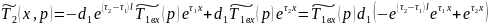
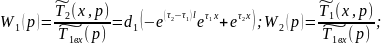
Для нахождения и необходимо использовать выражение (18) и (19).

Примечание: уравнения (7) и (8) нельзя преобразовывать по Лапласу по линейной координате, то есть они имеют различные граничные условия.

12. Вывод передат-х ф-ций конденсатора без учета накопл-я тепла в стенке.

Математическая модель имеет следующий вид:

где 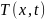– t-ра хладагента; 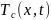— температура пара.

Нач-е усл-я для уравнения (1):

Граничные условия:

Структурная схема:

Второе граничное условие:

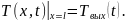
Преобразуем по Лапласу по времени при начальных условиях (2) уравнение (1):

, где символ преобразования по времени.

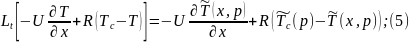
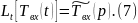
(7) является граничным условием для (6).

Преобразуем по Лапласу по линейной координате уравнение (6) с учетом граничных условий (7):

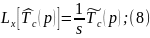
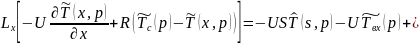
Прировняем (9) и (10):

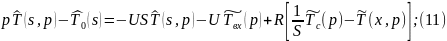
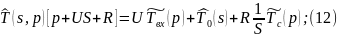
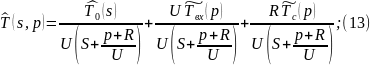
Применим обратное преобразование по Лапласу по линейной координате выражение (13):

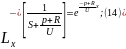
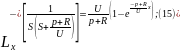
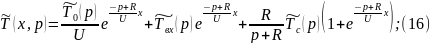
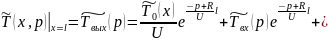
При значительной длительности режима :

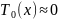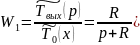
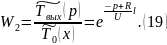
13. Вывод перед-х ф-ций конденсатора с учетом накопл-я тепла в стенке.

Математическая модель данного теплообменника имеет вид:

, ,

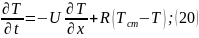
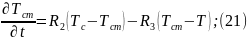
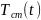
Начальные и граничные условия:

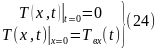
Преобразуем по Лапласу по времени (22), (23):

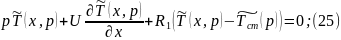
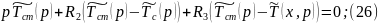
Преобразуем уравнение (25):

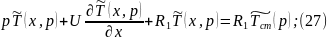
Преобразуем уравнение 4.5.26:

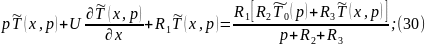
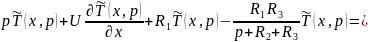
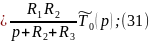
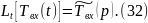
Уравнение (32) является граничным условием для (31).

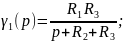
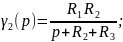
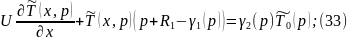
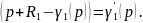
Преобразуем по Лапласу по линейной координате (33) при (32):

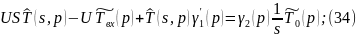
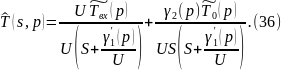
Пр-м обрат-е пр-е по Лапласу по лин-й корд-те уравнения (36):

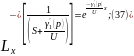
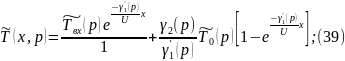
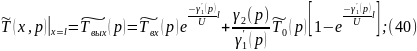
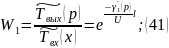
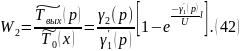
14. ПР-ПЫ ПОСТР-Я М/М-ЛЕЙ АНАЛИТ-МИ М-МИ.

Прим-тся 2 осн-х подхода по получ-ю М/М хим-техн-го проц-а:

1. Детерминистич-й подход осн-н на том, что механизм протек-я ХТП, созд-ся его теория на основе, кот пол-т м/м хтп.

Достоинства: можно спрогн-ть ход ХТП в любых усл-х. Недостатки: трудности разработки детерм-х моделей сложных ХТП и невозм-сть для некот-х ХТП получить детерм-х мм-лей. Если невозм. создать детерм-ю модель, то прим-ся 2-й подход:

2. Эмпирич-й. Получаемая модель наз-ся эмпир-й (статист-й).

Д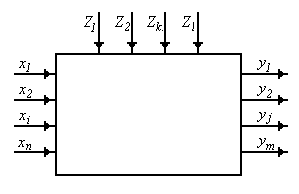 ля получ-я моделей прим-тся методы кибер-ки, осн-м из кот-х явл-тся метод, основ-й на схеме “черного ящика”. Всегда присутствует взаимод-е этого “черного ящика” с окруж-щей средой. Ряд взаимод-й, направл-х на “черный ящик”, наз-тся вх-ми воздействиями. Разл-т контролируемые вх-е возд-я и возмущающие воздействия. Также сущ-т вых-е результаты.

Для получ-я инф-и об объекте необх-о провести эксперимент.

; .

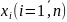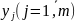Эксперимент состоит из отдельных опытов, рез-ты, кот-х записываются в таблицу.

Таблица 1

N
1
2
…	…	…	…	…	…	…
…	…	…	…	…	…	…
N

По данным таблицы 1 можно получить зависимость:

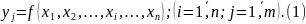
Полученная зав-сть наз-тся функцией отклика и является статистич-й матем-й моделью ХТП. Недостатки данного подхода:

1. малая надежность экстраполяции модели, то есть можно спрогн-ть значение только в пределах ;

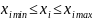2. данная модель не позв-т изучить механизм протекания, и она используется для решения экспериментальных задач.

Если ХТП является очень важным для химической технологии, то целесообразно применять детерминированный подход. Если ХТП является осень сложным, то для целей управления процессом целесообразно разработать статистическую модель. Если ХТП является и важным и сложным, то получение модели осуществляется в два этапа:

1. разработка статистической модели;

разработка детерминированной модели.