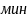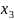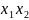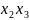5. Определение коэффициентов уравнения регрессии:

Если (2) дифференцируема, то коэф-нты можно определить с помощью метода наименьших квадратов, математическая формулировка которого имеет вид:

Данный функционал обеспечивает минимум квадрата разности между измеренным и рассчитанным значением вых-й величины. Для получ-я минимума необходимо:

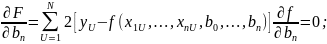
Преобразуем:

(4) явл-тся системой норм-ных ур-ний. В общем виде данная система не решается.

17. Оценка значимости коэф-в ур-я регрессии. 18. Оценка адекват-сти ур-я регрессии.

Используем для реш-я задачи получ-я ур-ния регрессии вычисл-я в матрич-й форме.

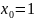фикт-я в-на. Рез-ты пасс-го эксп-нта предст-м в форме:

Решим (6) в матричной форме. Транспонируем (2):

Домножим (11) на

;

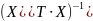
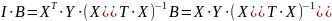
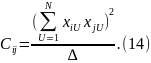
где 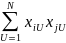- алг-е дополн-е любого эл-нта матрицы ;

— определитель матрицы (8).

6. Оценка значимости получ-х коэф-в выполняется по след-му нерав-ву.

или 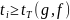, где

— среднеквадратичное отклонение коэффициента :

где — соотв-щий диаг-й элемент обратной матрицы (12).

—среднеквадратичное отклонение выходной величины .

— табличное значение критерия Стьюдента для и .

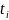Для всех рассчит-ся в-на и далее по выраж-ю (15) произв-ся оценка значимости . Если нерав-во вып-ся, то явл-ся значимым и наоборот. Если неск-ко коэф-ов не соотв-т нерав-ву (15), то вначале счит-ся коэф-нт незначимых для кот-го было наименьшим; данный пар-тр исключ-ся из матрицы исх-х данных, а все ост-ные коэф-ты пересчит-ся заново, т.к. переменные связаны между собой кор-ной связью. Процедура пров-ся до тех пор, пока все будут значимые.

7. Проверка адекватности уравнения регрессии. Для оценки исп-тся неравенство:

где – расчет-е знач-е вых-й вел-ны для усл-й i-того опыта. – фактич-е знач-е.

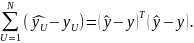
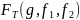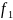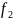— табличное значение критерия Фишера, которое выбирается из таблиц при и числе степеней свободы числителя уравнения 2.7.26 и — числе степеней свободы знаменателя .

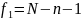Если неравенство 2.7.26 выполняется, то полученное уравнение 2.7.9 является адекватным.

Если неравенство 2.7.26 на выполняется, то полученное уравнение регрессии 2.7.9 является неадекватным.

19. Ортогон-е планы 1-го порядка.

Акт-й эксперимент провод-ся по заранее составл-му плану при этом одновременно варьируются все , что дает возм-сть сохранить число опытов по сравн-ю с пассивным. Каждому актив-му экспер-нту соот-ет вид регрессии. Для получения линейных ур-ний регрессии прим-тся ортогон-й метод 1-го порядка (симплекс планир-е, дробный и т.д.). Для получ-я нелин-х ур-ний регрессии прим-ся ортогон-й план 2-го пор-ка, центр-е композ-е планы, рототабельные м-ды, оптим-е планы и др.

1. Полный факторный эксперимент (пфэ).

В данном эксперим-те переем-е принимают 2 знач-я, при этом реализ-тся всевозмож-е комбинации из перем-х на 2х ур-нях, то такой экспер-нт наз-ся ПФЭ. .

Пример: предположим, что для некот-го объекта изуч-ся влияние 3х переменных:

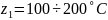(температура) 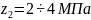(давление) 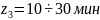(время преб-я)

Выходной параметр — выход конечного продукта .

Среднее значение:

Применение переменные в безразмерныймасштаб: .

Количество опытов: Составим матрицу:Таблица 2.3

№	,	,	,				, %
1	100	2	10	-1	-1	-1	2

Перепишем Таблицу 2.3, введя в неё столбец фиксированной переменной .

№					, %
1	+1	-1	-1	-1	2

где ур-ние 3. Представляет собой сумму скалярных произвед-й 2х любых векторов-столбцов матрицы ПФЭ равных 0. Данное св-во наз-ся св-вом ортогональности.

По плану ПФЭ можно получить следующие уравнения регрессии:

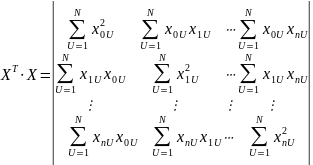(см. формулу) с учетом свойств примет вид:

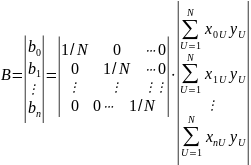
Вычисл-й алгоритм м-м ПФЭ сод-т три обязательных проверки:На воспроизводительность опытов эксперимента;На значимость коэффициентов , , ;На адекватность ур-я вида (32) на экстремальных данных.

Составляется следующие соотношение:

где — макс-я дисперсия, рассчит-я по формуле 2.7.36.

где 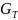– табл-е знач-е критерия Кохрена, кот-е выбир-ся из таблиц распред-я Кохрена и — числа степеней свободы и .

Если (38) вып-тся, то ПФЭ считается воспроизводимым и его данные считаются достоверными. Причина невоспроводимости может быть малое число опытов 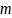. Если ПФЭ воспроизводим, то можно определить дисперсию вопроизводимости:

1. Проверка на значимость , ,

В виду ортогон-сти матриц ПФЭ, обратная матрица будет диаг-ной, при этом диаг-ные эл-нты будут одинак-ми. Это зн., что для всех ур-ний регрессии также будет одинакова и равна: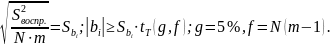

Если (42) не вып-ся, то коэф-нт счит-ся стат-ски незначимым и искл-ся из ур-ния (32) без пересчета, т.к. в силу ортог-сти матрицы ПФЭ эл-нты не св-ны кор-ной связью

Проверка уравнения регрессии 2.7.32 на адекватность.

Для решения этой задачи составим неравенство:

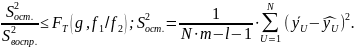
где — кол-во значимых коэф-в в уравнении регрессии; — расчетное знач-е выхода для усл-й -ого опыта экспер-та.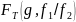 для

Если (43) вып-ся, то получ-е ур-ние вида (32) явл-ся адекватным. Если (43) не выполняется, то уравнение вида (32) является не адекватным. Необх-о прим-ть ортог-й план 2 порядка.

Дробный факторный эксперимент (ДФЭ) Если при мат-м мод-и объекта м огран-ся лин-м ур-м регрессии след-го вида: то вместо ПФЭ можно применять ДФЭ. Чтобы ДФЭ был ортогон-м планом 1го порядка, необх в кач-ве ДФЭ принять ближайший к нему ПФЭ, но с меньшим числом опытов.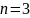 — ПФЭ; — ДФЭ ПФЭ= ( ).

Выр-е (47) наз-ся генер-щим. Постр-м матрицу ДФЭ для 3х перем-х: Таблица 2.5

№
1	+1	-1	-1	+1

Переп-м таблицу 2.5, введя в неё соотв-щие столбцы произв-й. Таблица 2.6

№
1	+1	-1	-1	+1	+1	-1	-1

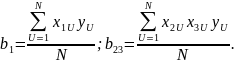
1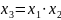. (см. таблицу 2.6), то есть коэффициент 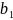является совместной оценкой . : . : .

Умножим соотношение (47) на : 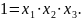Это соотн-е наз-тся опред-щим контрастом ДФЭ. Он позволяет опр-ть какие столбцы в матрице ДФЭ явл-ся одинаковыми, т.е., какие коэффициенты уравнения регрессии являются раздельными оценками, а какие являются смешанными.
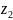