1. Модель динамики об-в рег-ния уровня в-ва.

С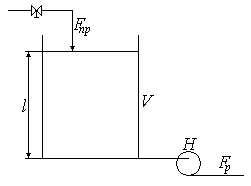 лучай А: Ж-ть подается в резервуар самотеком ч/з клапан, а вых-т из резервуара откачиванием насосом пост-й производ-сти.

где 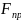– притока; — расхода.

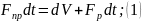
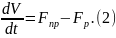
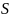— площадь сеч-я резервуара, ; 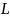-ур-нь.

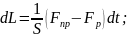
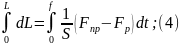
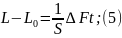
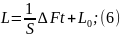
Для расчета АСР М/М объекта необх. представить в безразм-й форме:

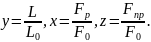
Подст-м в (3) введ-е обозначения:

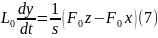
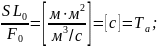
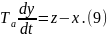
Прин-м 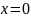: Если , то

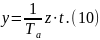
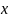можно принять = 0, так как ур-ие (3) можно записать в приращениях , .

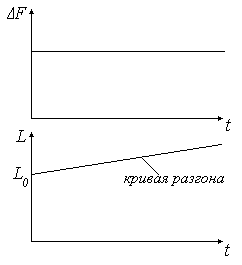
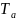– вр. разгона объекта (то вр., за кот-е относ-е измен-е рег-мой вны станет равным относму измен-ю возм-щего воздействия).

Преобр-уем по Лапласу при нулевых нач-х усл-ях по вр. ур-ние (9): 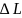при 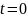будет = 0.

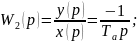
Случай В: Ж-сть подается в резервуар самотеком и отводится из резервуара самотеком по трубопроводу с клапаном.

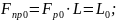
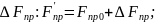
В-на расхода ж-сти опр-ся как в-ной уровня, так и проходным сеч-м. – коэф-нт пропорц-сти клапана; — площадь проходного сечения.

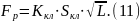
можно линеаризовать, разложив в ряд Тейлора:

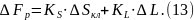
где

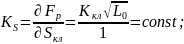
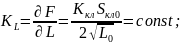
Составим уравнение материального баланса следующего вида:

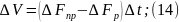
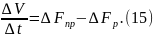
Ур-е 15 подставим в 13:

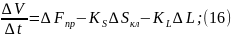
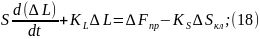
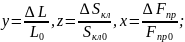
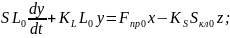
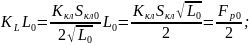
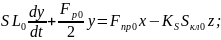
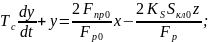
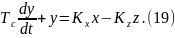
Начальные условия для (9) нулевые.

Преобразуем по Лапласу по времени (19):

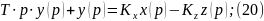
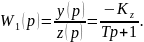
2. Модель дин-ки об-та рег-ния расхода в-ва.

С лучай А: Объект рег-ния участок трубопровода 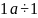г:

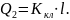
где — коэф-т пропорц-сти клапана; 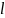– перем-е клапана.

Т. к. ж-сть полностью заполняет сеч-е трубопровода, то изменение 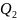на ту же вел-ну изменяет , то есть .

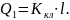
Запишем (1) в безразмерной форме:

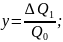
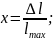
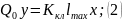
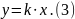где

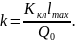
Выражение (3) преобразуем по Лапласу при :

С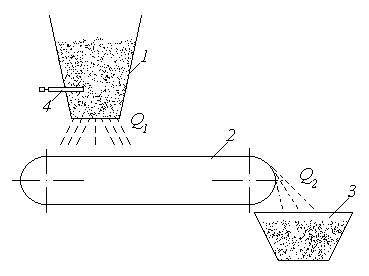 лучай В:

4 - шибер (заслонка).

Лента конвейера перем-ся со скоростью .

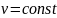При равномерной загрузке ленты транспортера определяется как:

где 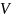- объем мат-ла; – раб-я дли-на от места сброса из бункера 1 в место сброса в бункер 3.

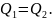
В мом-нт вр мы увелич-ем степень открытия шибера, при этом получим:

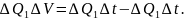
В начальный период .

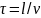Для отрезка времени : .

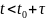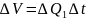Для отрезка времени : .

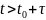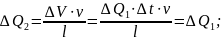
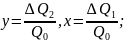
3. Модель дин-ки об-тов рег-ния конц-ции в-в.

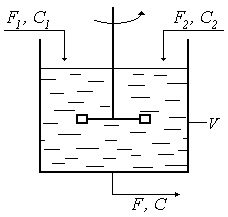— объемные скорости потоков;

– конц-и в-ва. - объём смесителя. Предп-ся, что .

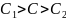Переменными в-ми являются .

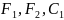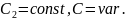
Для нахожд-я ур-ния динамики об-кта сост-м ур-ние мат-го баланса по конц-м в-в за время :

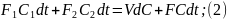
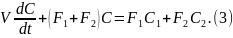
Данное ур-е явл-ся нелин-м ДУ-нием, поэтому приведем это уравнение, к линейному виду заменив все переменные величины суммой их значений в стационарном режиме к приращением:

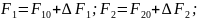
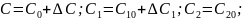
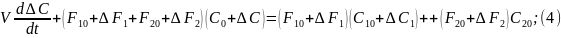
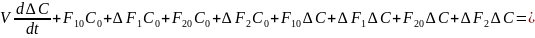
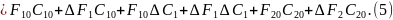
Запишем уравнение (3) для стационарного режима:

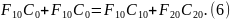
Вычтем из (5) уравнение (6):

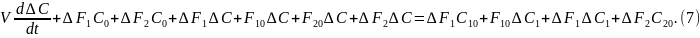
Так как приращение переменных малы, то и их произведения мало, то есть приблизительно равно нулю.

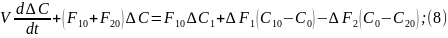
Выражение (8) представим в безразмерных величинах:

Разделим на коэф-нт при :

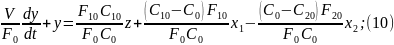
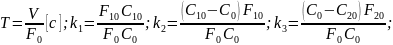
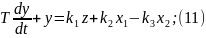
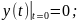
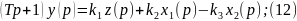
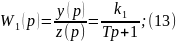
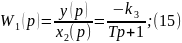
4. Модель идеал-го перемешивания.

З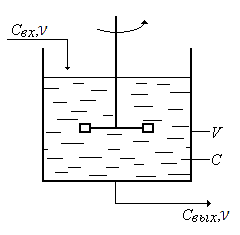 а стр-ру потока соотв-щую модели ид-го перемеш-я приним-т след-е:

Поток среды, поступ-й в аппарат, мгновенно распр-ся по всему объему ап-та и конц-я в-ва в каждой точке аппарата и на его выходе одинакова.

где 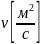– объемная скорость; – объем зоны ид-го переем-я;

Для стац-го режима: , ,

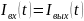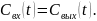
Для нестац-х р-мов:

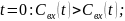
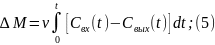
где 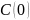– конц-я в уст-шимся режиме.

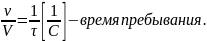
Продифференцируем (7) по времени:

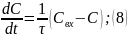
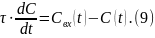
Преобразуем по Лапласу при нулевых нач-х усл-х выраж-е (9):

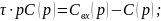
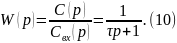
Решение уравнения 10 зависит от вида 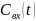. Если:

1. , то

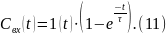
Выражение (11) называется F-кривой.

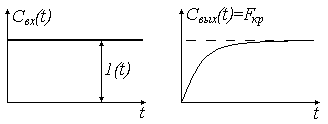
2. , то

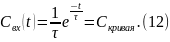
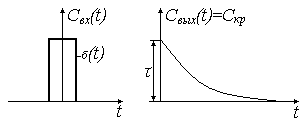
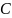Если при исследовании неизвестной структуры потока, получ-е экспериментальные и кривой совпадают с расчетными, то модели можно отнести к модели идеального перемешивания.

На практике часто стремясь получить модель ид-го перемеш-я, снабжаются их мешалками. Наиболее лучшему режиму идеального перемешивания соответствуют ёмкостные аппараты, проточного типа снабженные мешалками при небольшой объемной скорости и при условии .
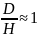