8. Разложение функций в степенные ряды. Ряд Тейлора. Ряд Маклорена. Разложение функции в степенные ряды

Рассмотрим степенной ряд для все х, принадлежащих области сходимости ряда, его сумма является функцией от х

В общем случае представляется функцией f(x) в виде степенного ряда производится на основе формулы Тейлора. Рядом Тейлора функции f(x0 в точке x₀. Называется степенной ряд

F(x₀)+f¹(x₀)(x-x₀)+ f²(x₀)(x-x₀)²…+ (x₀)(x-x₀)ⁿ+…= fⁿ(x₀)(x-x₀)ⁿ

Следует отметить, что ряд Тейлора для функции f(x) может расходится. Более того, … для сходящегося ряда Тейлора его сумма может не совпадать со значениями функции f(x). Необходимое и достаточное условие совпадения суммы сходящегося ряда Тейлора со значением самой функции формулируется следующая теорема.

Для того, чтобы ряд Тейлора функции f(x) в точке х, сходился к значению самой этой функции f(x) при х=х₁, необходимо и достаточно, чтобы член P_xn(х₁) стремится к нулю при n→∞

Формула Тейлора:

Пусть функция y=f(x) определена в некоторой окрестности X₀ и имел в ней производные до порядка n+1 включительно. Тогда для всего x из этой окрестности справедливо равенство.

(1)F(x)=f( )+ (x- )+ * +…+ +

Где с – некоторая точка из интервала ( ;x)

Формулой Тейлора для функции f(x) в окрестности точки называется формула (1) многочленном для функции f(x) в окрестности точки называется многочлен (x)=f( )+ (x- )+ (x- )+…

Остаточным членом формулы Тейлора называется слагаемое в форме Тейлора

(x)= =f(x)-P_n(x)

Таким образом, многочлен Тейлора P_n (x) служит приближение формулы f(x). Оценкой этого приближения служит остаточный член формулы Тейлора P_n(x).

Формула Маклорина

Формула Маклорина для функции f(x) называется ее формулой Тейлора при x₀=0

F(x)=f(0)+ x+ x²+…+ xⁿ+ xⁿ⁺¹

Где с некоторая точка из интервала (0,x)

9. Применение степенных рядов для приближенных вычислений: интегрирование функций, вычисление пределов.

Тема 3. Дифференциальные уравнения

10. Общее и частное решения дифференциального уравнения. Общий и частный интегралы.

Обыкновенным дифференциальным уравнением первого порядка называется уравнение вида

F(x, y, y' )=0,     

где F — известная функция трех переменных, определенная в области G из R³,   x — независимая переменная из интервала (a, b), y(x) — неизвестная функция, y'(x) — ее производная.  

Обыкновенные дифференциальные уравнения, разрешенные относительно производной, т.е. уравнения вида 

y'=f(x, y)

Функция y=y(x) называется решением дифференциального уравнения, если она непрерывно дифференцируема на (a, b) и при всех x из (a, b) удовлетворяет уравнению F(x, y(x), y'(x))=0.

График решения дифференциального уравнения называют интегральной кривой дифференциального уравнения.

Если дифференциальное уравнение первого порядка y'=f(x, y), имеет решение, то   решений у него, вообще говоря, бесконечно много и эти решения могут быть записаны в виде y=y(x,C), где C — произвольная константа. Выражение y(x,C) называют общим решением дифференциального уравнения 1-го порядка: при всех допустимых значениях C функция y=y(x,C) является решением уравнения, y'(x,C)=f(x, y(x, C)); для любого наперед заданного решения y=x) найдется такое значение константы C, C=С*, что y(x,C*)=x).  

Однако, если поставить задачу: найти решение, удовлетворяющее условию y(x₀)=y₀, то при определенных условиях такая задача имеет единственное решение.  Задача об отыскании решения y=y(x) дифференциального уравнения y'=f(x, y), удовлетворяющего начальному условию y(x₀)=y₀, называется задачей Коши. Решение задачи Коши называют частным решением.

11. Общим решением дифференциального уравнения (12.1) 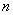–го порядка называется такое его решение 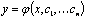, которое является функцией переменных 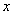 и  произвольных постоянных .

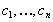12. Частным решением дифференциального уравнения называется решение, получаемое из общего решения при некоторых конкретных числовых значениях постоянных

Любое конкретное решение y = φ(x) уравнения n –го порядка F(x, y(x), y '(x), y ''(x),  …  , y^{(n )}(x)) = 0, называется частным решением.

 

Общим решением дифференциального уравнения

F(x, y(x), y '(x), y ''(x),  …  , y^{(n )}(x)) = 0

называется функция

y = Ф(x,  С₁, С₂, … , С_n),

содержащая некоторые постоянные (параметры) С₁, С₂, … , С_n, и обладающая следующими свойствами:

1. Ф(x, С₁, С₂,  … , С_n) является решением уравнения при любых допустимых значениях С₁, С₂, … , С_m;

2. для любых начальных данных  y(x₀) = y₀,  y '(x₀) = y₁,  y ''(x₀) = y₂,  …  , y^{(n − 1)}(x₀) = y_{n − 1}, для которых задача Коши имеет единственное решение,

существуют значения постоянных С₁ = A₁, С₂ = A₂,  … , С_n = A_n, такие что решение y = Ф(x, A₁, A₂,  …, A_n) удовлетворяет заданным начальным условиям.

Иногда частное или общее решение уравнения удается найти только в неявной форме: f(x, y) = 0 или G(x, y, С₁,  С₂,  ..., С_n) = 0.

Такие неявно заданные решения называются частным интегралом или общим интегралом уравнения.