4. Знакопеременные ряды. Достаточный признак сходимости знакопеременного абсолютно сходящегося ряда. Абсолютно сходящиеся ряды. Условно сходящиеся ряды.

Обобщенный геометрический ряд

при а>1 является сходящимся

а≤1 ряд расходящийся

Признаки Коши:

Пусть для числового ряда с положительными членами существует =λ

Тогда:

А) если λ<1, то ряд сходится

Б) если λ1, то ряд расходится

Пример:

Для числового ряда с положительными членами

Найдем предел

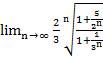= = = <1

Знакопеременные ряды:

Знакопеременным называется числовой ряд , содержащий бесконечно много положительных слагаемых и бесконечно много отрицательных слагаемых.

Числовой ряд является знакопеременным.

Достаточный признак сходимости знакопеременного ряда.

Знакопеременный ряд сходится, если сходится ряд, составленный из модулей его членов.

(A₁) ₊ (A₂) +…+(A_n)= () – это модуль

Абсолютно сходящимся называется знакопеременный ряд , для которого ряд, составленный из модулей его членов, , является сходящимся.

Условно сходящимся, называется сходящийся знакопеременный ряд, составленный из модулей его членов , расходится.

Пример:

Знакопеременный ряд является абсолютно сходящимся, так как ряд сходится.

Знакочередующий ряды:

Знакочередующимся называется числовой ряд

А₁-а₂+а₃-…(-1)ⁿ⁺¹an= an

Где an>0 для всех n∈N

5. Знакочередующиеся ряды. Признак Лейбница.

Признак Лейбница.

Знакочередующий ряд an сходится, если a₁a₂>…>an>

Пример:

Знакочередующий ряд

1- удволетворяет условиям признака Лейбница, поэтому он сходится. Однако ряд из модуля его членов 1- является гармоническим и расходящимся. Таким образом исходный ряд является сходящимся.

Тема 2. Степенные ряды

6. Степенные ряды. Интервал, радиус сходимости.

Степенным рядом называется ряд вида

C₀+C₁X+C₂X²+C_nXⁿ+…= , где c_n – некоторые числа, Х-переменная. Коэффициентом степенного ряда называется числа С₀,С₁,…_,С_n,…

Пример:

1+х+х²+…+хⁿ+…= степенной ряд, все его коэффициенты равны 1. При каждом конкретном значении переменной степенной ряд становится числовым рядом, к которому применены все понятия и результаты, в частности, понятия абсолютной сходимости. Областью сходимости степенного ряда называется множества всех значений переменной х, при которых соответствующий числовой ряд сходится.

Степенной ряд в предыдущим примере является бесконечной суммой членов геометрической прогрессии со знаменателям Х. его частная сумма S_n= Эта сумма имеет конечный предел при <1. Поэтому область сходимости исходного ряда является интервал (-1;1)

7. Свойства степенных рядов.

Теорема Абеля

1. Если степенной ряд сходится при некотором значении х=х₀≠0, то он сходится абсолютно при всех значениях 

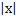
2. Если степенной ряд расходится при х=х₁, то он расходится при всех значениях х, таких что 

Из теоремы Абеля следует, что существует такоe число R≥0, что при R сходится, а при >R ряд расходится. Вопрос о сходимости ряда при х=±R требует дополнительных исследований. Радиусом сходимости степенного ряда называется такое число R≥0, что ряд сходится при <R и расходится при >R. Радиусом сходимости степенного ряда, при С_n≠≠0 находится по формуле