25

1. Определение сходимости числового ряда. Свойства сходящихся рядов. Числовые ряды

Числовыми рядами называются бесконечная последовательность чисел, соединенных знаком сложения: U₁+U₂+…+U_n+…= Числа U₁U_2… называются членами ряда, член U_n – общим или n-ым членом ряда, сумма n-первых членов ряда.

S_n=U₁+U₂+…+U_n= называются частной суммой ряда.

Ряд называется сходящимся, если существует конечный предел последовательности его частичных сумм, т.е S=

Число S называется суммой ряда. Если конечного предела, последовательности частичного сумм не существует, то ряд называется расходящимся.

Отбрасывание или приписывание к ряду конечного числа членов не влияет на сходимость или расходимость ряда.

Пример Покажем, что ряд + + = сходится. Возьмем сумму S_n первых n членов ряда. S_n= + +…+ . Слагаемые этой суммы могут быть представлены в виде =1- ; = - ; = - ;…; = - . Поэтому S_n=(1-- )+( - - )+…+( - )=1- Отсюда следует, что предел последовательности членов числительных сумм данного ряда равен единице.

)=1- Ряд сходится, его сумма S=1

Пример 2.

Установим сходятся или расходятся ряды.

1-1+1-1+…+(-1)^n-1+…=

Последовательность его частных сумм имеет вид S₁=1, S₂=0, S₃=1, S₄=0… и значит, не сходится ни к какому пределу, поэтому данный ряд расходится.

Пример 3.

Рассмотрим ряд, составленный из элементов геометрической прогрессии:

a +aq+aq²+ aq³+…+ aq^n-1+…= ,a≠0

Частичная сумма S_n этого ряда при q≠1 имеет вид S_n = a +aq+aq²+ aq³+…+ aq^n-1= = -

Отсюда:

1. еслиq1, то 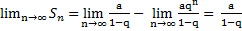т.е ряды сходятся и его сумма S=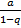

например, при a=1,q= имеет:

S=1+ + +… +…=2

2. еслиq1, то 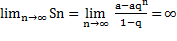, ряд расходится

3. если q=1 ряд принимает вид a+a+a+…a+…

В этом случае: , ряд расходится

4. при q=-1 ряд принимает вид a-a+a-a+… Для него S_{n = -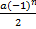} – , т.е S_n=0 при n четном и S_n =a при n нечетном. Следовательно, S_n не существует и ряд расходится. Таким образом, ряд является сходящимся приq<1 и расходящимся при q1

2. Необходимое условие сходимости числового ряда.

Если ряд сходится, то предел его общего члена при n→∞ равен нулю . При нарушении необходимого условия сходимости ряда, т.е если предел общего члена ряда при n→∞, не существует или если он не равен нулю, ряд расходится. Заметим, что если предел общего члена ряда равен нулю, то вывод о сходимости или расходимости ряда можно сделать только после дополнительного исследования.

Пример:

Гармонический ряд

1 + +…+ +…= этот ряд расходящийся

Пример: обобщенный гармонический ряд

1+ + +…+ +…=

Где α -некоторое число

Этот ряд сходится, если α 1 и расходится если α≤ 1.

Пример

3+

Является расходящимся, поскольку его общий член a_n= не стремится к нулю.

3. Ряды с неотрицательными членами. Достаточные признаки сходимости: признаки сравнения, Даламбера, Коши, интегральный признак.

Признаки сходимости числовых рядов с положительными членами.

Пусть имеется два числовых ряда с положительными членами.

a₁+a₂+…+a_n+…(1)

b₁+b₂+…+b_n…(2)

где a_n>0,b_n>,для всех n∈N. Для таких рядов справедливы следующие признаки сходимости.

Признаки сравнения.

Пусть общие члены рядов (1) и (2) (с положительными членами) связаны неравенством a_n≤b_n, для всех n∈N.

Тогда:

1. Если ряд (2) сходится, то и ряд (1) сходится

2. Если ряд (1) расходится, то и ряд (2) расходится

При применении признака сравнения обычно в качестве эталонных рядов рассматриваются следующие ряды.

1. Сумма членов геометрической прогрессии

2. Гармонический ряд

3. Обобщенные гармонический ряд

Пример:

1) =2+ + + +

Является расходящимся, так как его общий член b_n= больше общего члена a_n= расходящегося гармоничного ряда.

2)Члены числового ряда положительны. Сравним их с членами обобщенного гармонического ряда. сходится, то по признаку сравнения сходится и сходный ряд.

Признак Даламбера

Пусть для числового ряда c положительными членами предел отношения последующего члена к предыдущему равен λ: тогда,

1. Если λ<1, то ряд сходится

2. Если λ>1, то ряд расходится

3. Если λ=1, то ряд может сходиться, а может и расходится

Примеры:

1. Числовой ряд 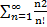является сходящимся. Для него 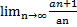= =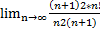 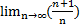²*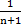

0<1

По признаку Даламбера ряд сходится

2. Числовой ряд 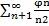( все в степени) расходится. Для него =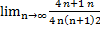 (n+1 в числителе-это степень, а n,2 в знаменателе – это степень)=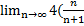 )2 (в степени)=4>1 - По признаку Даламбера ряд расходится

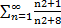3. Для числового ряда имеем = =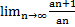

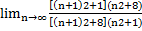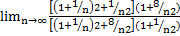
Признак Даламбера не позволяет выяснить вопрос о сходимости ряда, однако этот ряд является расходящимся по необходимому признаку.

=1≠0

Предельный признак сравнения

Пусть и ряды с положительными членами и существует конечный предел отношения их обоих членов.

=μ≠0

Тогда ряда одновременно сходятся или расходятся.

Пример:

Для числовых рядов и рядов предел отношения общих членов равен =1≠0

Поскольку первый ряд как обобщенный гармонический сходится , то по предельному признаку сравнения сходится и второй ряд.

Интегральный признак сходимости

Пусть все члены числового ряда и не возрастают а₁≥а₂≥…≥a_n≥…

Пусть существует непрерывно возрастающая функция у=f(x) , опр. При всех x≥1, такая что f(1)=a₁; f(2)=a₂… f(a_n)=a_n , тогда для сходимости числового ряда необходимо и достаточно, чтобы сходился несобственный интервал dx

Пример:

Для α>1 члены обобщенного гармонического ряда «+» и не возрастают.

Рассмотрим функцию f(x)= . Для х≥1эта функция непрерывна и не возрастает, кроме того f(n)= , т.е для нее выполнены все интегрального признака сходимости.

Несобственный интеграл является сходящимся при а>1

Действительно, по определению сходимости несобственного интеграла имеем:

= = * = =0+ <∞

Поэтому обобщенный гармоничный ряд

при α>1, является сходящимся