§ 7 Наибольший общий делитель многочленов. Алгоритм Евклида.
О1)Общим делителем многочленов f(x) и g(x) называется такой d(x) что, выполняются f(x)⋮d(x) и g(x)⋮d(x).
О2)Наибольшим будет тот из общих делителей степень которого больше.
Будем считать что, общий делитель d(x) который делится на любой другой делитель этих многочленов будет наибольшим d(x)=(f(x),g(x)) очевидно что, общим делителем многочленов будет и делитель вида: с*d(x)=(с*f(x),с*g(x)),c=const 0.
НОД отыскивается с точностью до
постоянного множителя. Многочлены
отличающееся друг от друга постоянным
множителем называются ассоциированными.
НОД отыскивают с помощью алгоритма
Евклида который состоит в следующем: с
начал делят с остатком многочлен f(x)
на g(x) затем
g(x) на остаток
от первого деления затем
от первого деления на остаток 
от второго деления и так далее до тех
пока не получится нулевой остаток при
этом получается цепочка равенств.
Последний не нулевой остаток и есть НОД двух многочленов.
Пример 1:
В кольце R[x] найти НОД двух многочленов:
|
|
|
|
|
|||
|
|
|
|
|
|
||
|
|
|
|
|
|
||
|
|
|
|
|
|||
|
|
|
|
|
|
||
|
|
|
|
|
|||
.
На практике может возникнуть задача отыскания нескольких многочленов:
НОД(f,g…q)=НОД(f,НОД(g,…НОД(t,q)…)).
Т1:НОД двух многочленов может быт
представлен в виде: 
Где 
из тогоже кольца что, и данные многочлены.
Доказательство:
Для нахождения НОД(f,g) воспользуемся равенствами 1 алгоритма Евклида:
подставляя это равенство во второе
равенство совокупности 1 можем выразить
остаток
.
действуя так и далее можно выразить
остаток 
через f(x) и
g(x) а, также
последний остаток 
.
Пример 2:
Из примера 1 запишем представление остатков:
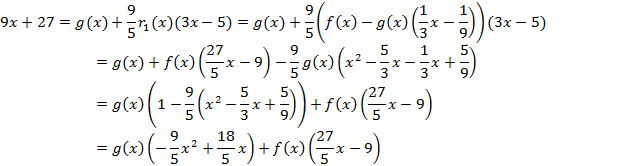
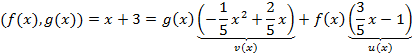
§ 8 Наименьшее общее кратное двух многочленов.
О1) Многочлен
называется общим кратным для 
и 
если 
.
О2)Общее кратное f(x)
и g(x)
на которое делится любое общее кратное
этих многочленов называется наименьшим
общим кратным многочленов
и
и обозначается: 
.
Т1:Для любых многочленов 
существует наименьшее общее кратное
которое можно найти по формуле 
Доказательство:
Пусть многочлен 
некоторое произвольное общее кратное
многочленов f(x)
и g(x). Так
как М общее кратное то M(x)=f(x)p(x),
M(x)=g(x)q(x)
(f(x),g(x))=d(x),
тогда 
g(x)⋮d(x)
Из этого равенства видно, что 
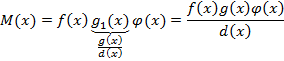
Получено выражение для произвольного общего кратного многочленов f(x) g(x) положив в этом выражении 𝜑(x)=1 получим формулу для нахождения наименьшего общего кратного.
Замечание:
[f,g]⋮f
[f,g]⋮g
M⋮[f,g]