13 Вопрос:

Если число строк матрицы равно числу столбцов, то есть m = n, то матрицу называют квадратной порядка n. Квадратные матрицы, у которых отличны от нуля лишь элементы главной диагонали, называются диагональными матрицами.

Квадратная матрица называется треугольной, если все элементы, стоящие выше (или ниже) главной диагонали, равны нулю. Транспонированием называется такое преобразование матрицы, при котором строки и столбцы меняются местами с сохранением их номеров. Обозначается транспонирование значком Т наверху.

Пусть дана матрица (4.1). Переставим строки со столбцами. Получим матрицу

AT = ,

которая будет транспонированной по отношению к матрице А. В частности, при транспонировании вектора-столбца получается вектор-строка и наоборот.

Произведением матрицы А на число λ называется матрица, элементы которой получаются из соответствующих элементов матрицы А умножением на число λ: λA = ( λaij).

Суммой двух матриц А = (aij) и B = (bij) одного размера называется матрица C = (cij) того же размера, элементы которой определяются по формуле cij = aij + bij.

Произведение АВ матрицы А на матрицу В определяется в предположении, что число столбцов матрицы А равно числу строк матрицы В.

Произведением двух матриц А = (aij) и B = (bjk), где i = , j= , k= , заданных в определенном порядке АВ, называется матрица С = (cik), элементы которой определяются по следующему правилу:

cik = ai1b1k + ai2b2k + ... + aimbmk = aisbsk. (4.2)

Иначе говоря, элементы матрицы-произведения определяются следующим образом: элемент i-й строки и k-го столбца матрицы С равен сумме произведений элементов i-й строки матрицы А на соответствующие элементы k-го столбца матрицы В.

Пусть нам дана квадратная матрица порядка n

. (4.3)

Рассмотрим все возможные произведения по n элементов этой матрицы, взятых по одному и только по одному из каждой строки и каждого столбца, т.е. произведений вида:

, (4.4)

где индексы q1, q2,..., qn составляют некоторую перестановку из чисел

1, 2,..., n. Число таких произведений равно числу различных перестановок из n символов, т.е. равно n!. Знак произведения (4.4) равен (- 1)q, где q - число инверсий в перестановке вторых индексов элементов.

Определителем n -го порядка, соответствующим матрице (4.3), называется алгебраическая сумма n! членов вида (4.4). Для записи определителя употребляется символ ‌ A ‌ = или det A= (детерминант, или определитель, матрицы А).

14 Вопрос:

Метод Гаусса:

Наиболее известным и популярным точным способом решения систем линейных алгебраических уравнений (СЛАУ) является метод Гаусса. Этот метод заключается в последовательном исключении неизвестных. Пусть в системе уравнений

первый элемент a11(0) не равен 0. Назовем его ведущим элементом первой строки. Поделим все элементы этой строки на a11(0) и исключим x1 из всех последующих строк, начиная со второй, путем вычитания первой (преобразованной), умноженной на коэффициент при x1 в соответствующей строке. Получим

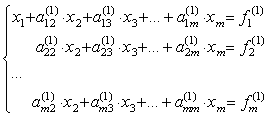
Если a22(1), то, продолжая аналогичное исключение, приходим к системе уравнений с верхней треугольной матрицей

Из нее в обратном порядке находим все значения xi:

Процесс приведения к системе с треугольной матрицей называется прямым ходом, а нахождения неизвестных - обратным. Если один из ведущих элементов равен нулю, изложенный алгоритм метода Гаусса неприменим. Тем не менее, для нормальной матрицы с ненулевым определителем всегда возможна такая перестановка уравнений, что на главной диагонали не будет нулей. В приведенном коде для простоты перестановок не делается, зато делается проверка решения, а прямой и обратный ход для наглядности вынесены в отдельные подпрограммы.

Метод Крамера:

Для системы n линейных уравнений с n неизвестными (над произвольным полем)

с определителем матрицы системы Δ, отличным от нуля, решение записывается в виде

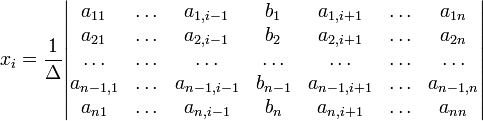
(i-ый столбец матрицы системы заменяется столбцом свободных членов). В другой форме правило Крамера формулируется так: для любых коэффициентов c₁, c₂, …, c_n справедливо равенство:

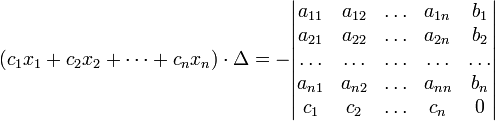
В этой форме формула Крамера справедлива без предположения, что Δ отлично от нуля, не нужно даже, чтобы коэффициенты системы были бы элементами целостного кольца (определитель системы может быть даже делителем нуля в кольце коэффициентов). Можно также считать, что либо наборы b₁,b₂,...,b_n и x₁,x₂,...,x_n, либо набор c₁,c₂,...,c_n состоят не из элементов кольца коэффициентов системы, а какого-нибудь модуля над этим кольцом. В этом виде формула Крамера используется, например, при доказательстве формулы для определителя Грама и Леммы Накаямы.