- •1 Вопрос: Определение множества
- •Основные числовые множества
- •Элементы логической символики
- •Операции над множествами
- •4 Вопрос:
- •Угловой коэффициент в уравнении прямой. Геометрический смысл коэффициента.
- •5 Вопрос:
- •10 Вопрос:
- •11 Вопрос:
- •12 Вопрос:
- •Основные действия над матрицами
- •Операция умножения матриц
- •13 Вопрос:
- •14 Вопрос:
- •15 Вопрос:
- •16 Вопрос:
- •Основные теоремы о пределах
- •17 Вопрос:
- •18 Вопрос: Асимптота
- •19 Вопрос: Непрерывная функция
- •21 Вопрос: Производная
- •22 Вопрос: Дифференциал функции
- •23 Вопрос:
- •24 Вопрос:
- •25 Вопрос:
- •26 Вопрос:
- •27 Вопрос: теоремы о дифференцируемых функциях
- •28 Вопрос:
- •29 Вопрос: Выпуклые и вогнутые функции
- •Проверка функции на выпуклость
- •Вогнутая функция
- •Проверка функции на вогнутость
- •30 Вопрос:
28 Вопрос:
Правило
Бернулли[1]-Лопита́ля —
метод нахождения пределов
функций,
раскрывающий
неопределённости
вида 0 / 0
и
![]() .
Обосновывающая метод теорема утверждает,
что при некоторых условиях предел
отношения функций
равен пределу отношения их производных.
.
Обосновывающая метод теорема утверждает,
что при некоторых условиях предел
отношения функций
равен пределу отношения их производных.
Условия:
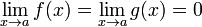 или
или
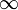 ;
;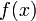 и
и
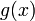 дифференцируемы
в проколотой окрестности
дифференцируемы
в проколотой окрестности
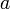 ;
;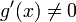 в
проколотой окрестности
;
в
проколотой окрестности
;существует
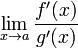 ,
,
тогда существует
![]() .
.
Пределы также могут быть односторонними.
29 Вопрос: Выпуклые и вогнутые функции
Введем обозначение: x=(x1,x2,:,xn) - n-мерный вектор.
Определение:
n мерная функция f(x), определенная на выпуклом множестве D, называется выпуклой функцией тогда и только тогда, когда для любых двух точек x(1) и x(2) принадлежащих D, и любого числа L (0<=L<=1) выполняется неравенство:
f(Lx(1) +(1-L)x(2))<=Lf(x(1))+(1-L)f(x(2))
Проиллюстрируем определение выпуклой функции для случая одной переменной:
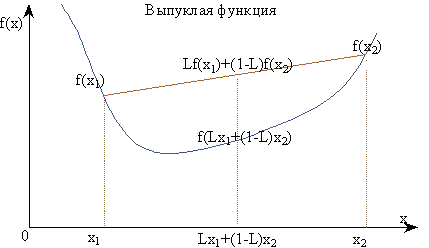
Свойства выпуклых функций:
Хорда, соединяющая две любые точки кривой графика выпуклой функции, всегда проходит над (или выше) кривой в интервале между двумя этими точками.
Выпуклая функция лежит над своими касательными
Тангенс угла наклона касательной, или первая производная f(x), возрастает или, по крайней мере, не убывает при увеличении x.
Вторая производная f(x) всегда не отрицательна на рассматриваемом интервале.
Для выпуклой функции локальный минимум всегда является глобальным минимумом.
Градиент функции f(x1,x2,:,xn) определяется как вектор:
С f(x1,:,xn)=(df/dx1,df/dx2,:,df/dxn)T
Матрица Гессе(гессиан) для функции f(x1,:,xn) есть симметрическая матрица порядка n*n:
Hf(x1,:,xn)=[d2f/dxidxj]=С2f
Проверка функции на выпуклость
Функция f(x1,:,xn) выпуклая, если ее матрица Гессе положительно определена или положительно полуопределена для всех значений x1,x2,:,xn.
Для функции одной переменной: функция f(x) выпуклая, если ее вторая производная неотрицательна для всех значений x:
d2f/dx2=>0, для всех x
Если матрица Гессе Hf - положительно определенная матрица, то f называется строго выпуклой функцией и обладает единственной точкой минимума.
Вогнутая функция
Функция f(x1,:,xn) является вогнутой функцией на множестве D тогда и только тогда, когда -f(x) есть выпуклая функция на D.
Проверка функции на вогнутость
Функция f(x1,:,xn) вогнутая, если ее матрица Гессе отрицательно определена, или отрицательно полуопределена для всех значений x1,:,xn.
30 Вопрос:
Непрерывная на отрезке [a; b] функция f (x) называется выпуклой вверх на этом отрезке, если для любых точек x1 и x2 из этого отрезка
|
|
||||||||||
Аналогично определяется функция, выпуклая вниз.
Дважды
дифференцируемая на [a; b]
функция f (x)
выпукла вверх, если для любого
Дважды дифференцируемая на [a; b] функция f (x) выпукла вниз, если для любого
Так, вторая
производная функции
Пусть функция
f (x)
непрерывна в точке
Необходимое условие наличия точки перегиба. Если – точка перегиба функции f (x), и функция f (x) имеет вторую производную, непрерывную в этой точке, то
Достаточные условия наличия точки перегиба.
Пусть функция
f (x)
непрерывна и имеет конечную или
бесконечную производную в точке
Если
В заключение приведем примеры, когда точка x0 не является точкой перегиба несмотря на то, что ее вторая производная меняет знак при переходе через эту точку:
Не являются
точками перегиба и точки
возврата,
например точка
Все вышеперечисленные случаи изображены на рисунке.
31 ВОПРОС:
Тейлора формула формула
изображающая функцию f (x), имеющую n-ю производную f (n)(a) в точке х = а, в виде суммы многочлена степени n, расположенного по степеням х—а, и остаточного члена Rn (x), являющегося в окрестности точки а бесконечно малой более высокого порядка, чем (x—a) n [то есть Rn (x) = an (x)(x—a) n, где an (x) → 0 при х → а]. Если в интервале между а и х существует (n + 1)-я производная, то Rn (x) можно представить в видах:
, где ξ и ξ1 — какие-то точки указанного интервала (остаточный член Т. ф. в формах Лагранжа и соответственно Коши). График многочлена, входящего в Т. ф.. имеет в точке а Соприкосновение не ниже n-го порядка с графиком функции f (x). Т. ф. применяют для исследования функций и для приближённых вычислений.
32 ВОПРОС:
Первообразная и неопределенный интеграл Первообразной функцией для функции f(x) называется такая функция F(х), производная которой равна данной функции F'(x) = f(x). Обозначение
где F'(x) = f(x). Функция f(x) называется подынтегральной функцией, а выражение f(x)dx - подынтегральным выражением.
33 ВОПРОС:
Свойства неопределенного интеграла 1°. Производная неопределенного интеграла равна подынтегральной функции; дифференциал от неопределенного интеграла равен подынтегральному выражению, т.е.
2°. Неопределенный интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной постоянной, т.е.
3°. Постоянный множитель можно вынести из под знака интеграла, т.е. если k = const ≠ 0, то
4° . Неопределенный интеграл от алгебраической суммы двух функций равен алгебраической сумме интегралов от этих функций в отдельности.
34 ВОПРОС:
Метод замены переменной в неопределенном интеграле Переходим к рассмотрению общего случая – метода замены переменных в неопределенном интеграле. Пример 5
Найти неопределенный
интеграл.
В качестве примера
я взял интеграл, который мы рассматривали
в самом начале урока. Как мы уже
говорили, для решения интеграла нам
приглянулась табличная формула
Идея метода
замены состоит в том, чтобы сложное
выражение (или некоторую функцию)
заменить одной буквой.
В
данном случае напрашивается:
Итак:
Действие следующее.
После того, как мы подобрали замену,
в данном примере,
,
нам нужно найти дифференциал
Так как , то
После разборок
с дифференциалом окончательный
результат рекомендую переписать
максимально коротко:
В итоге:
Чистовое оформление рассмотренного примера должно выглядеть примерно так:
“
Проведем замену:
Значок
Также всем
рекомендую использовать математический
знак
При оформлении
примера в тетради надстрочную пометку
Внимание! В следующих примерах нахождение дифференциала расписываться подробно не будет.
А теперь самое
время вспомнить первый способ
решения:
В чем разница? Принципиальной разницы нет. Это фактически одно и то же. Но с точки зрения оформления задания метод подведения функции под знак дифференциала – гораздо короче. Возникает вопрос. Если первый способ короче, то зачем тогда использовать метод замены? Дело в том, что для ряда интегралов не так-то просто «подогнать» функцию под знак дифференциала.
Интегри́рование по частя́м — один из способов нахождения интеграла. Суть метода в следующем: если подынтегральная функция представима в виде произведения двух непрерывных и гладких функций (каждая из которых может быть как элементарной функцией, так и композицией), то справедливы следующие формулы для неопределённого интеграла:
для определённого:
Предполагается,
что нахождение интеграла
Получение формул для неопределённого интеграла
Функции
Эти функции также непрерывны, значит можно взять интеграл от обеих частей равенства:
Операция интегрирования обратна дифференцированию:
После перестановок:
Не стоит, однако, забывать, что это равенство подразумевается в смысле равенства множеств, то есть, грубо говоря, с точностью до константы, возникающей во время интегрирования. Типичную ошибку «потери» константы при обращении с неопределенным интегралом иллюстрирует следующий пример-софизм:
Отсюда «следствие»: 0 = 1, что очевидно неверно. для определённого В целом аналогично случаю неопределённого интеграла:
35 ВОПРОС:
Интегрирование рациональных функций
Для интегрирования
рациональной функции
Рассмотрим указанные шаги более подробно. Шаг 1. Преобразование неправильной рациональной дроби Если дробь неправильная (т.е. степень числителя P(x) больше степени знаменателя Q(x)), разделим многочлен P(x) на Q(x). Получим следующее выражение:
где - правильная рациональная дробь. Шаг 2. Разложение знаменателя на простейшие дроби Запишем многочлен знаменателя Q(x) в виде
где квадратичные функции являются несократимыми, то есть не имеющими действительных корней. Шаг 3. Разложение рациональной дроби на сумму простейших дробей. Запишем рациональную функцию в следующем виде:
Общее число неопределенных коэффициентов Ai , Bi , Ki , Li , Mi , Ni , ... должно быть равно степени знаменателя Q(x). Затем умножим обе части полученного уравнения на знаменатель Q(x) и приравняем коэффициенты при слагаемых с одинаковыми степенями x. В результате мы получим систему линейных уравнений относительно неизвестных коэффициентов Ai , Bi , Ki , Li , Mi , Ni , .... Данная система всегда имеет единственное решение. Описанный алгоритм представляет собой метод неопределенных коэффициентов. Шаг 4. Интегрирование простейших рациональных дробей. Простейшие дроби, полученные при разложении произвольной правильной рациональной дроби, интегрируются с помощью следующих шести формул:
У дробей с квадратичным знаменателем сначала необходимо выделить полный квадрат:
где
Интеграл
36 ВОПРОС:
Определение
определённого интеграла.
Пусть на отрезке [a,b]
задана функция y
= f(x).
Разобьём отрезок [a,b]
произвольным образом на n
частей точками [x0
,
x1],
[x1
,
x2],
…, [xi-1
, xi],
…, [xn-1
, xn];
длину i-го
отрезка обозначим
Как следует из
пункта 11.1.1,
если f(x)
>0 на отрезке [a,b],
то
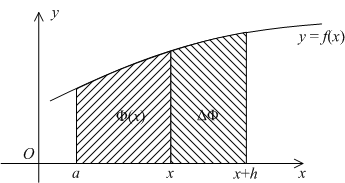
37 ВОПРОС: Интеграл с переменным верхним пределом
Рассмотрим
функцию
определена при
всех
Теорема
3.11
Функция
,
определённая выше, непрерывна при
всех
Доказательство.
Заметим, что если функция
положительна,
то значение
интерпретируется
как площадь под графиком
Рис.3.4.
Эта площадь,
вследствие ограниченности интегрируемой
функции, мала, если приращение
мало;
это и означает непрерывность функции
Проведём теперь более аккуратные рассуждения, не предполагая, что функция принимает положительные значения.
Пусть фиксирована
точка
Согласно неравенству (3.5),
Но по теореме
3.5
функция
ограничена,
поэтому существует такая постоянная
откуда
При
Рассматривая
аналогично отрезок
при , что означает непрерывность функции слева в любой точке .
Тем самым функция
непрерывна
справа в точке
Теорема
3.12
Пусть
функция
непрерывна
на отрезке
и
функция
определена
всё той же формулой. Тогда
имеет
производную в любой точке интервала
Доказательство.
Снова рассмотрим приращение
где
откуда при из непрерывности следует, что
поскольку
Аналогично
доказывается, что левая производная
Точно так же доказывается, что производная интеграла
от непрерывной
функции
по
переменному нижнему пределу равняется
Равенство
Итак, мы получили важный результат о наличии первообразной у любой непрерывной функции:
Теорема
3.13
Пусть
--
непрерывная на интервале
функция.
Тогда на интервале
функция
имеет
некоторую первообразную
Доказательство.
Для доказательства достаточно
фиксировать произвольную точку
При
Нетрудно видеть,
что при
Пусть теперь
где
поскольку
где -- произвольная первообразная для функции . Эта формула называется формулой Ньютона - Лейбница. Она играет ключевую роль в интегральном исчислении и во всём математическом анализе. Напомним, что мы получили её в предположении, что функция непрерывна. Если функция имеет разрыв на отрезке , то разность значений первообразной может не иметь никакого отношения к величине определённого интеграла. Поэтому при применении формулы Ньютона - Лейбница нужно строго следить за законностью этого действия.
Смысл формулы
Ньютона - Лейбница (3.6)
состоит в том, что для нахождения
определённого интеграла
Итак, формула Ньютона - Лейбница устанавливает связь между определённым интегралом от данной функции и первообразной для этой функции, то есть между определённым и неопределённым интегралами. Заметим, что смысл этих двух понятий первоначально совершенно различен: неопределённый интеграл -- это набор функций (первообразных), а определённый интеграл -- это число (равное пределу интегральных сумм).
При вычислениях
разность
часто
называют подстановкой
в функцию
пределов
и
и
обозначают
а формулу Ньютона - Лейбница можно записать в виде
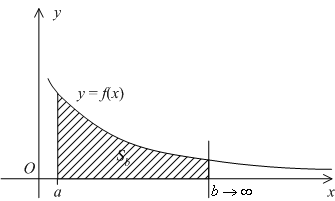
Несобственные интегралы первого рода
Определение
4.1
Предположим, что функция
задана
на бесконечном промежутке вида
Если эта функция
имеет предел
а сам интеграл
Если же предела
Геометрически,
в случае
Рис.4.1.
Сходящиеся интегралы соответствуют таким областям , площадь которых конечна (хотя сама область неограничена), а расходящиеся (в случае ) -- неограниченным областям с бесконечной площадью. В случае, когда при , часто пишут формально:
однако нужно ясно понимать, что эта запись означает расходимость интеграла и отсутствие у него числового значения.
Само определение
значения интеграла через предел
интегралов по конечным, но увеличивающимся
отрезкам означает исчерпание площади
Рис.4.2 Глава 3. Признаки сходимости и расходимости несобственных интегралов Теорема 1. Пусть фиксировано число и функция интегрируема на любом отрезке , где . Тогда если несобственный интеграл сходится, то при любом сходится интеграл . Обратно, если при некотором сходится интеграл , то сходится и интеграл . Теорема 2 (теоpема сpавнения) Пусть даны две функции и , заданные на , причём при всех выполняется неравенство Тогда из сходимости интеграла от большей функции, , следует сходимость интеграла от меньшей функции, , причём а из расходимости интеграла от меньшей функции, , следует расходимость интеграла от большей функции, : Геометрически доказанное утверждение почти очевидно: оно означает, что если площадь под верхним графиком на следующем рисунке (она заштрихована), конечна, то конечна и имеет меньшее значение площадь под нижним графиком (она имеет двойную штриховку). Рис. 5. Если условие неотрицательности функций и не предполагается, то оба утверждения теоремы могут оказаться не верны: так, если взять и при всех , то интеграл от большей функции, оказывается сходящимся (его значение, очевидно, равно 0), а интеграл от меньшей функции, -- расходится (докажите расходимость, вычислив интеграл и рассмотрев его поведение при ). При помощи теоремы 2 можем в некоторых случаях исследовать сходимость интеграла, не вычисляя его значения. Для доказательства сходимости интеграла от функции достаточно найти более простую функцию , для которой интеграл легко вычисляется и сходится. Согласно теореме, тогда исходный интеграл тоже сходится, причём мы получаем оценку его величины: . Если же нам нужно доказать расходимость интеграла , то достаточно найти такую (более просто устроенную) функцию , что и интеграл расходится. Признак сходимости Абеля: 1. пусть функции f(x) и g(x) определены в промежутке , причём f(x) интегрируема в этом промежутке, т.е. интеграл сходится (условно или абсолютно); 2. g(x) монотонна и ограничена: . Тогда интеграл сходится. Признак сходимости Дирихле: 1. пусть функция f(x) интегрируема в любом конечном промежутке [a, b], и интеграл по этому промежутку ограничен (как функция верхнего предела b): ; 2. g(x) монотонно стремится к нулю при : . Тогда интеграл сходится. Эталонные интегралы Пример 2. Рассмотрим интеграл Если , то подынтегральная функция стремится к при , так что получается несобственный интеграл второго рода. Рассмотрим такие случаи: 1) . Тогда интеграл вычисляется так: поскольку при имеем и 2) . Тогда то есть интеграл расходится, поскольку при . 3) . Тогда и интеграл снова расходится, поскольку при , если показатель . Заметим также, что при интеграл не является несобственным: это обычный (то есть собственный) интеграл от непрерывной ограниченной функции. Единственная неприятность получается при , поскольку тогда подынтегральная функция не определена при (и тождественно равна 1 при ). Но мы знаем, согласно одному из свойств определённого интеграла, что значение подынтегральной функции в одной точке можно изменить без изменения значения интеграла. Так что достаточно переопределить значение в 0, положив и получив собственный интеграл Пример 3. Определим, при каких значениях показателя интеграл cходится. Рассмотрим случай . Тогда Поскольку при Значит, при интеграл сходится и имеет значение Рассмотрим случай . Тогда поскольку (то есть предела не существует) и . Значит, при интеграл расходится. Рассмотрим случай . Тогда поскольку при Значит, при интеграл расходится. Итак, интеграл сходится (и функция определена и равна ) только при ; при интеграл расходится. Теорема 3. Если интеграл сходится, то сходится также интеграл причём имеет место неравенство
|
|||||||||||
График 3.2.3.1. Выпуклая вверх функция. |
|||||||||||

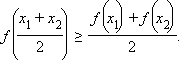
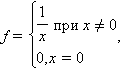
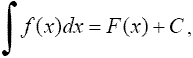
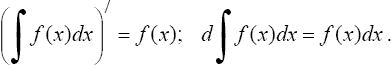
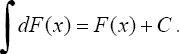
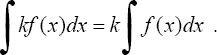
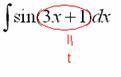 Но
при замене у нас остаётся
Но
при замене у нас остаётся
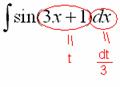 Таким
образом:
Таким
образом:
 Готово.
Готово.
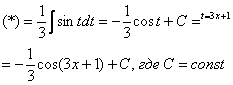 “
“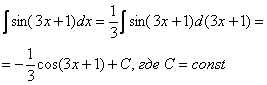
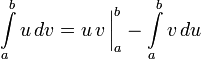
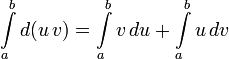
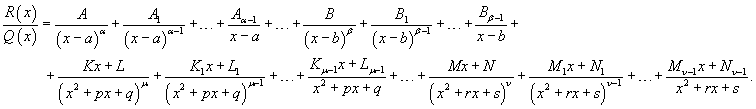
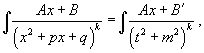
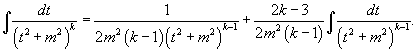
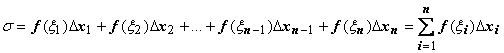 .
.
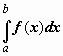 .
Функция
f(x),
как и в случае неопределённого
интеграла, называется подынтегральной,
числа a
и b
- соответственно, нижним и верхним
пределами интегрирования.
Кратко
определение иногда записывают так:
.
Функция
f(x),
как и в случае неопределённого
интеграла, называется подынтегральной,
числа a
и b
- соответственно, нижним и верхним
пределами интегрирования.
Кратко
определение иногда записывают так:
 .
В
этом определении предполагается, что
b>
a.
Для других случаев примем, тоже по
определению:
Если b=a,
то
.
В
этом определении предполагается, что
b>
a.
Для других случаев примем, тоже по
определению:
Если b=a,
то
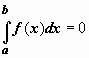 ;
если b<a,
то
;
если b<a,
то
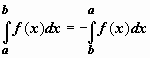 .
.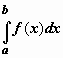 равен
площади криволинейной трапеции ABCD,
ограниченной снизу отрезком [a,b],
слева и справа - прямыми x
= a
и x
= b,
сверху – функцией y
= f(x).
равен
площади криволинейной трапеции ABCD,
ограниченной снизу отрезком [a,b],
слева и справа - прямыми x
= a
и x
= b,
сверху – функцией y
= f(x).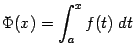
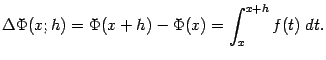
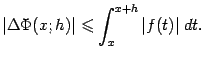
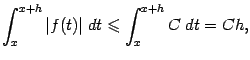
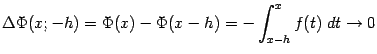
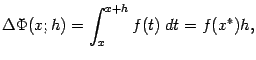
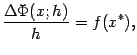
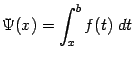
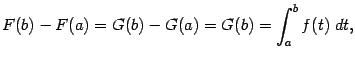
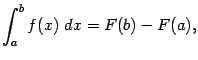
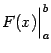 .
Таким образом, по определению,
.
Таким образом, по определению,
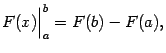
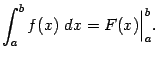
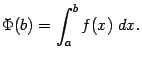
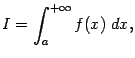
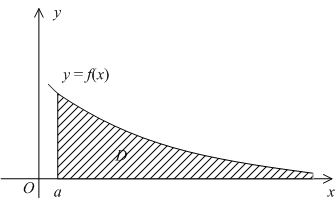
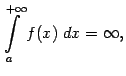
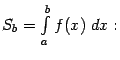 правый
вертикальный отрезок, проведённый
при
,
отодвигается всё дальше и дальше в
бесконечность; в пределе будет учтена
вся площадь под графиком
(см. рис.).
правый
вертикальный отрезок, проведённый
при
,
отодвигается всё дальше и дальше в
бесконечность; в пределе будет учтена
вся площадь под графиком
(см. рис.).