
- •1 Вопрос: Определение множества
- •Основные числовые множества
- •Элементы логической символики
- •Операции над множествами
- •4 Вопрос:
- •Угловой коэффициент в уравнении прямой. Геометрический смысл коэффициента.
- •5 Вопрос:
- •10 Вопрос:
- •11 Вопрос:
- •12 Вопрос:
- •Основные действия над матрицами
- •Операция умножения матриц
- •13 Вопрос:
- •14 Вопрос:
- •15 Вопрос:
- •16 Вопрос:
- •Основные теоремы о пределах
- •17 Вопрос:
- •18 Вопрос: Асимптота
- •19 Вопрос: Непрерывная функция
- •21 Вопрос: Производная
- •22 Вопрос: Дифференциал функции
- •23 Вопрос:
- •24 Вопрос:
- •25 Вопрос:
- •26 Вопрос:
- •27 Вопрос: теоремы о дифференцируемых функциях
- •28 Вопрос:
- •29 Вопрос: Выпуклые и вогнутые функции
- •Проверка функции на выпуклость
- •Вогнутая функция
- •Проверка функции на вогнутость
- •30 Вопрос:
10 Вопрос:
Пусть даны векторы
![]() и
и
![]() .
Определение. Суммой векторов
.
Определение. Суммой векторов
![]() и
и
![]() называется
вектор
называется
вектор
![]() ,
т.е. при сложении векторов их соответствующие
координаты складываются: (2, –4) + (–2, 4)
= (0, 0); (3,0,1) + (0,1,4)+(–1, –7,0) = (2, –6,5).
Определение. Произведением вектора
,
т.е. при сложении векторов их соответствующие
координаты складываются: (2, –4) + (–2, 4)
= (0, 0); (3,0,1) + (0,1,4)+(–1, –7,0) = (2, –6,5).
Определение. Произведением вектора
![]() на
число
на
число
![]() называется
вектор
называется
вектор
![]() т.е.
при умножении вектора на число каждая
его координата умножается на это
число.
Можно проверить,
что введенные таким образом операции
над векторами удовлетворяют всем
свойствам операций в линейном пространстве.
Следовательно, арифметическое n-мерное
пространство Rn является
частным случаем введенного ранее
линейного пространства.
Определение. Скалярным произведением
двух векторов
т.е.
при умножении вектора на число каждая
его координата умножается на это
число.
Можно проверить,
что введенные таким образом операции
над векторами удовлетворяют всем
свойствам операций в линейном пространстве.
Следовательно, арифметическое n-мерное
пространство Rn является
частным случаем введенного ранее
линейного пространства.
Определение. Скалярным произведением
двух векторов
![]() и
и
![]() называется
число, равное сумме произведений
соответствующих координат векторов:
называется
число, равное сумме произведений
соответствующих координат векторов:
![]() Пример: Пусть
Пример: Пусть
![]() и
и
![]() .
Тогда
.
Тогда
![]() .
Скалярное произведение обладает
следующими свойствами:
1.
.
Скалярное произведение обладает
следующими свойствами:
1.![]() ,
причем
,
причем
![]() ,
только при
,
только при
![]() 2.
2.![]() ,
3.
,
3.![]() ,
4.
,
4.![]() .
Определение. Два вектора называются
ортогональными, если их скалярное
произведение равно 0, т.е.
.
Определение. Два вектора называются
ортогональными, если их скалярное
произведение равно 0, т.е.
![]() .
Пример. Пусть
.
Пример. Пусть
![]() Тогда
Тогда
![]() ортогональны.
Определение. Линейное пространство
с введенным скалярным произведением
называется евклидовым n-мерным
пространством.
Примеры:
1. Множество трехмерных векторов R3.
2. Множество
двумерных векторов R2.
3.
Множество R1 = R – множество
действительных чисел.
ортогональны.
Определение. Линейное пространство
с введенным скалярным произведением
называется евклидовым n-мерным
пространством.
Примеры:
1. Множество трехмерных векторов R3.
2. Множество
двумерных векторов R2.
3.
Множество R1 = R – множество
действительных чисел.
11 Вопрос:
Скалярное произведение
Скалярное
произведение векторов
![]() и
и
![]() :
:
![]()
где
![]() -
угол между векторами
-
угол между векторами
![]() и
;
если
и
;
если
![]() либо
либо
![]() ,
то
,
то
![]()
Из
определения скалярного произведения
следует, что
![]() где,
например,
где,
например,
![]() есть
величина проекции вектора
на
направление вектора
.
есть
величина проекции вектора
на
направление вектора
.
Скалярный
квадрат вектора:
![]()
Свойства
скалярного произведения:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Скалярное произведение в координатах
Если
![]()
![]() то
то
![]()
![]()
Угол между векторами
![]()
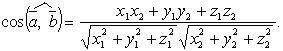
Векторное произведение
Векторное
произведение векторов
и
-
вектор, обозначаемый
![]()
![]() или
или
![]() для
когорого:
для
когорого:
1)
![]() (
- угол между векторами
и
,
(
- угол между векторами
и
,
![]() );
);
2)
![]()
3) тройка , , - правая.
Свойства
векторного произведения:![]()
![]()
![]()
![]()
![]()
![]() если
если
![]() ,
то
,
то
![]() равен
площади параллелограмма, построенного
на приведенных к общему началу векторах
и
.
равен
площади параллелограмма, построенного
на приведенных к общему началу векторах
и
.
Норма — структура длины векторов на линейном пространстве.
Норма в векторном
линейном
пространстве
![]() над
полем
вещественных
или комплексных
чисел
есть функция
над
полем
вещественных
или комплексных
чисел
есть функция
![]() ,
удовлетворяющая следующим условиям
(аксиомы нормы):
,
удовлетворяющая следующим условиям
(аксиомы нормы):
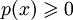 ,
причём p(x)
= 0 только
при
,
причём p(x)
= 0 только
при
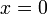 ;
;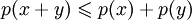 для
всех
для
всех
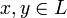 (неравенство
треугольника);
(неравенство
треугольника);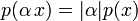 для
любого скаляра
α.
для
любого скаляра
α.
Норма
![]() обычно
обозначается
обычно
обозначается
![]() .
Линейное пространство с нормой называется
нормированным
пространством,
а условия (1-3) — также аксиомами
нормированного пространства.
.
Линейное пространство с нормой называется
нормированным
пространством,
а условия (1-3) — также аксиомами
нормированного пространства.
Аксиома 2 обеспечивает
выпуклость
шаров
![]() ,
аксиома 3 — кроме прочего, их центральную
симметрию.
,
аксиома 3 — кроме прочего, их центральную
симметрию.
Любой ненулевой вектор (в частности функцию) конечной нормы можно нормировать, поделив его на значение его нормы (после чего он станет нормированным). Также, нередко применяется выражение «нормированный на», подразумевающее, что норма объекта равна в этом случае не единице, а другой определенной величине. Например, иногда говорят о нормировании на дельта-функцию, когда речь идет о нормировании базиса функций, нумерованного непрерывным параметром.
