
- •Геометрические векторы. Линейные операции с векторами
- •Пример.
- •N10 Метрические соотношения в Rn
- •Преобразование матрицы линейного оператора при переходе к новому базису
- •N19 Определение собственного значения и собственного вектора линейного оператора
- •Общий случай Подпространство называется инвариантным подпространством линейного преобразования a (a-инвариантным подпространством), если
- •Определение собственного значения и собственного вектора линейного оператора
- •Общее уравнение в матричном виде
- •Гиперболоиды
Пример.
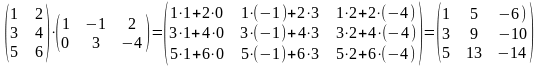 .
.
Для произведения матриц соответствующих порядков справедливо:
A·B ≠ B·A,
(A + B) · C = A·C + B·C,
C·(A + B) = C·A + C·B,
α(A·B) = (αA) ·B,
(A·B) ·C = A·(B·C),
(AB)T = B TA T,
 ,
A,
B
— квадратные матрицы одинаковой
размерности.
,
A,
B
— квадратные матрицы одинаковой
размерности.AE=EA=A, A— квадратная матрица, E — единичная матрица соответствующей размерности.
Если AB = BA, то матрицы A и B называются перестановочными.
Непосредственным вычислением легко проверить основное свойство единичной матрицы
Обратная матрица
Обратная матрица:
Определение: Матрица Х, удовлетворяющая вместе с заданной матрицей А равенствам XA=AX=En (1),
(где Еn – единичная матрица некоторого порядка n) наз. обратной к А и обозначается A–1.Поскольку А и A–1 перестановочны, они обе должны быть квадратными того же порядка n. Из (1) в силу того, что ранг произведения двух матриц не превосходит рангов сомножителей, мы имеем Rg EnRg A. Отсюда RgA=n. Поэтому матрица А может иметь обратную только тогда, когда её детерминант 0. Приведенное условие является не только необходимым, но и достаточным для существования обратной матрицы. Предложение: (1) Каждая квадратная матрица с детерминантом, отличным от нуля, имеет обратную матрицу, и притом только одну. Доказательство: Для каждой матрицы А с det A0 существует единственная матрица Х такая, что АХ=Е. Действительно, при любом j столбец xj матрицы Х должен удовлетворять условию Ахj=еj, где еj – j-й столбец единичной матрицы. Подробнее это условие записывается сист. линейных уравнений: (2)
a11xi1+...+a1nxjn=0 По правилу Крамера эта система
............................. уравнений имеет единственное
aj1xi1+...+ajnxjn=1 решение, и, => каждый столбец
............................. матрицы Х однозначно определен.
an1xi1+...+annxjn=0 Докажем, что ХА=Е. С этой целью заметим, что det X0 и по только что доказанному существует такая матрица Y, что XY=Е. Мы найдем Y, если умножим обе части последнего равенства слева на матрицу A. Тогда AХY=А, откуда в силу АX=Е следует Y=A. Итак, матрица Х удовлетворяет обоим условиям (1). Способ, примененный при доказат-ве существования, является основой для нахождения обратной матрицы. Согласно правилу Крамера i-я неизвестная в системе (2) находится по формуле хji=i/det A, где i – детерминант матрицы, получаемой из А заменой её i-го столбца на j-й столбец единичной матрицы. Разлагая i по этому столбцу, мы имеем только одно слагаемое, так как в ej только один элемент равен 1, а остальные – нули. =>, i = (–1)i+j Mij, где Mij – дополнительный минор элемента aij в матрице А. Окончательно:
xji = ((–1)i+j Mij)/det A, (3). Можно решать систему (2) и методом Гаусса.
N6 Элементарные преобразования матриц
Помимо операций с матрицами определены операции с элементами матриц, операции со столбцами и строками матрицы — так называемые элементарные преобразования матриц.
Определение. Элементарными преобразованиями матрицы называют следующие операции:
перестановка любых двух строк (столбцов) матрицы;
умножение любой строки (столбца) на произвольное, отличное от нуля, число;
сложение любой строки (столбца) с другой строкой (столбцом), умноженной (умноженным) на произвольное, отличное от нуля, число.
к элементарным преобразованиям иногда относят и операцию транспонирования матрицы.
Приведение матрицы к ступенчатому виду Гауссовым исключением
Утверждение. Любую прямоугольную матрицу можно с помощью элементарных преобразований привести к ступенчатой форме.
Это утверждение на лекции доказано.
Пример.
Приведем к ступенчатой форме матрицу.
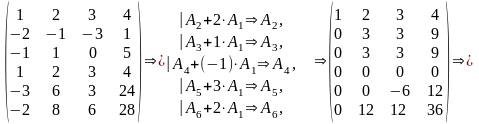
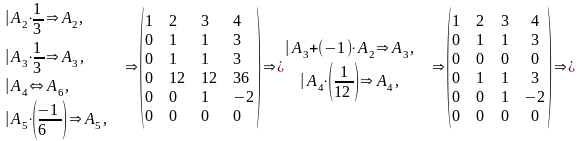
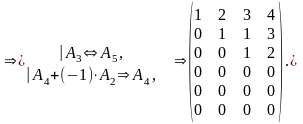
Алгоритм приведения матрицы к ступенчатой форме с помощью элементарных преобразований называют Гауссовым исключением или методом Гаусса.
N7 Линейное пространство:
Пространство арифметических векторов Rn
Определение.
Арифметическим
вектором называется упорядоченная
совокупность n
чисел. Обозначается
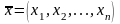 ,
числа
,
числа
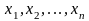 называются
компонентами арифметического вектора.
называются
компонентами арифметического вектора.
Для
арифметических векторов определены
линейные операции — сложение
арифметических векторов и умножение
вектора на число:
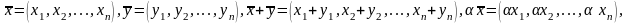 для
любых
для
любых
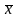 и
и
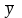 и
любого числа
и
любого числа
Определение. Множество арифметических векторов, для которых определены операции сложения и умножения на число называется пространством арифметических векторов Rn.
Вектор
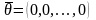 называется
нулевым вектором, а вектор
называется
нулевым вектором, а вектор
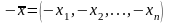 — противоположным вектором для вектора
.
— противоположным вектором для вектора
.
Для
любых
,
,
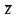 из Rn
и любых чисел
α
, β справедливо:
из Rn
и любых чисел
α
, β справедливо:
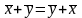 ,
сложение коммутативно;
,
сложение коммутативно;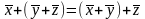 ,
сложение ассоциативно;
,
сложение ассоциативно;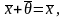
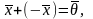
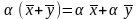 ,
умножение на число дистрибутивно
относительно сложения элементов;
,
умножение на число дистрибутивно
относительно сложения элементов;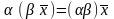 ,
умножение на число ассоциативно;
,
умножение на число ассоциативно;
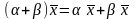 ,
умножение вектора на число дистрибутивно
относительно сложения чисел.
,
умножение вектора на число дистрибутивно
относительно сложения чисел.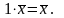
Примерами пространства арифметических векторов являются пространства геометрических векторов на плоскости, записанных в координатной форме.
N8 Линейная зависимость и линейная независимость в Rn
Определение.
Линейной
комбинацией векторов
 называется выражение
называется выражение
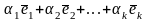 ,
где коэффициенты линейной комбинации
,
где коэффициенты линейной комбинации
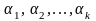 — некоторые числа.
— некоторые числа.
Определение.
Говорят,
что вектор
пространства Rn
линейно
выражается через векторы
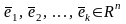 ,
если его можно представить в виде
линейной комбинации этих элементов
,
т.е. представить в виде
,
если его можно представить в виде
линейной комбинации этих элементов
,
т.е. представить в виде
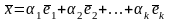 .
.
Определение.
Система
векторов из Rn
называется линейно
независимой
если из
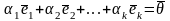 следует равенство нулю всех коэффициентов
следует равенство нулю всех коэффициентов
 ,
,
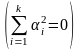 .
.
Иными
словами, линейная комбинация векторов
равна нулю тогда и только тогда, когда
все
коэффициенты линейной комбинации равны
нулю.
Определение. Система векторов, которая не является линейно независимой, называется линейно зависимой.
Иными
словами, существуют такие коэффициенты
линейной комбинации
,
не все равные нулю
 ,
что
.
,
что
.
Или: линейная комбинация векторов может обратиться в нуль, хотя не все коэффициенты линейной комбинации равны нулю.
Свойства линейно зависимых и линейно независимых систем функций
Любая система векторов, содержащая нулевой вектор линейно зависима.
Любая система векторов, содержащая пару взаимно противоположных векторов — линейно зависима.
Любая система векторов, содержащая два равные вектора — линейно зависима.
Любая подсистема линейно независимой системы векторов — линейно независима.
Если некоторая подсистема системы векторов линейно зависима, то и вся система — линейно зависима.
Необходимое и достаточное условие линейной зависимости системы векторов в Rn
Справедливо следующее утверждение.
Теорема (Необходимое и достаточное условие линейной зависимости системы векторов). Система векторов из Rn линейно зависима тогда и только тогда, когда хотя бы один вектор системы векторов из Rn линейно выражается через остальные векторы системы.
Базис в Rn. Координаты вектора в заданном базисе. Линейные операции в координатной форме
Определение. Система векторов из Rn образует базис в Rn если:
система векторов упорядочена;
система векторов линейно независима;
любой вектор из Rn линейно выражается через векторы системы.
Иными
словами, линейно независимая упорядоченная
система векторов
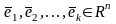
Образует
базис в Rn
если любой
вектор
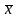 из Rn
может быть
представлен в виде
из Rn
может быть
представлен в виде
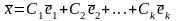 .
.
Определение.
Выражение
называется разложением вектора в базисе
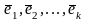 ,
а числа
,
а числа
 называются координатами вектора
в базисе
.
называются координатами вектора
в базисе
.
Теорема (о единственности разложения вектора в базисе). Для любого вектора из Rn разложение вектора в базисе единственно
Теорема. В пространстве Rn существует базис из n векторов.
Действительно,
этот базис — естественный базис
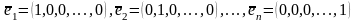
Линейные подпространства:
Определение: Непустое множество L' векторов в линейном пространстве L наз. линейным подпространством если: а) сумма любых векторов из L' принадлежит L', б) произведение каждого вектора из L' на любое число также принадлежит L'. =>можно доказать, что в силу этого определения любая линейная комбинация векторов из L' принадлежит L'. В частности, нулевой вектор, как произведение 0x, должен лежать в L' Точно так же для каждого вектора х из L' противоположный вектор, равный — 1x, лежит в L'. Сложение и умножение на число, определенные в пространстве L будут такими же операциями в его подпространстве L', Справедливость аксиом линейного пространства для L' прямо вытекает из их справедливости в L, т.о. каждое линейное подпространство само является линейным пространством. Предложения: (1) Размерность линейной оболочки конечного множества векторов не превосходит числа этих векторов. (2) Пусть L' – подпространство n-мерного линейного пространства Ln. Тогда L' имеет размерность k n. Если k=n, то L' совпадает с Ln. (3) Пусть L' – подпространство в n-мерном пространстве L. Если базис e1, ..., ek, ek+1, ..., ek в L, то в базисе e1, ..., ek все векторы из L' и только такие векторы будут иметь компоненты k+1=0, ..., k=0. (4)Пусть в n-мерном пространстве L выбран базис. Тогда координатные столбцы векторов, принадлежащих k-мерному подпространству L', удовлетворяет однородной системе линейных уравнений ранга n–k (при L'=L сист. имеет 0-ой ранг, т.е. не содержит ни одного нетривиального уравнения).
N9 Ранг матрицы и метод её вычисления:
Определение: В матрице А размеров тn минор порядка r наз. базисным, если он отличен от нуля, а все миноры порядка r+1 равны нулю или миноров порядка r+1 вообще нет, т.е. r совпадает с меньшим из
чисел т или п. Ясно, что в матрице может быть несколько разных базисных миноров. Все базисные миноры имеют один и тот же порядок. Действительно, если все миноры порядка r+1 равны нулю, то равны нулю и все миноры порядка r+2, а =>, и всех больших порядков. Это становится очевидным, если применить определение детерминанта к какому-нибудь минору порядка r+2; все дополнительные миноры элементов его первой строки являются минорами порядка r+1 нашей матрицы и, следовательно, равны нулю. Столбцы и строки, на пересечении которых расположен базисный минор, мы назовем базисными столбцами и строками. Определение: Рангом матрицы наз. порядок базисного минора, или, иначе, самый большой порядок, для которого существуют отличные от нуля миноры. Если каждый элемент матрицы равен нулю, то ранг такой матрицы, по определению, считают нулем. Ранг матрицы А мы будем обозначать Rg A. Перебирать все миноры в поисках базисного – задача, связанная с большими вычислениями, если размеры матрицы не очень малы. Проще всего находить ранг матрицы и её базисный минор при помощи элементарных преобразований. Предложения: (1) Элементарные преобразования не меняют ранга матрицы. Доказательство: [1] При умножении строки на число 0 базисный минор либо не изменится, либо умножится на . Ни один минор, равный 0, не сделается отличным от 0. [2] Если все миноры порядка r+1 равны нулю, то сложение строк не сделает ни один из них отличным от 0. Действительно, полученный после преобразования минор либо равен алгебраической сумме двух миноров порядка r+1 исходной матрицы (в том случае, когда к строке, входящей в минор, прибавили строку, в него не входящую), либо он равен сумме минора порядка r+1 и детерминанта матрицы с двумя одинаковыми строками (в том случае, когда к строке, входящей в минор, прибавили другую строку, в него входящую). Из этих соображений следует, что ранг матрицы не может повыситься. Ясно, что он не может и понизиться, так как в противном случае при обратном преобразовании – вычитании строк – он бы повысился. [3] При перестановке строк минор может изменить (если в него входят обе переставляемые строки), или может замениться на минор, не больше чем знаком отличающийся от другого минора той же матрицы (если содержит только одну из переставляемых строк), или вообще не изменится. Ясно, что при этом порядок базисного минора останется тем же. [4] Неизменность ранга при элементарных преобразованиях столбцов доказывается аналогично. Элементарные преобразования строк матрицы будут для нас предпочтительнее ввиду их тесной связи с преобразованиями систем линейных уравнений. Для системы из m уравнений с п неизвестными:
a11x1+...+a1nxn=b1 расширенная ||a11...a1n b1||
............................. матрица A*=||....................||
amx1+...+amnxn=bm имеет вид: || am1...amn bm||
Перестановке строк этой матрицы соответствует изменение порядка уравнений в системе. Умножение строки на число 0 равносильно умножению соответствующего уравнения на это число. Наконец, прибавить в матрице A* к одной строке другую – то же самое, что сложить соответствующие уравнения системы. При всех этих преобразованиях множество решений системы, разумеется, не меняется. Итак, доказано. (2) Элементарным преобразовазованиям строк расширеной марицы соответствуют преобразования системы линейных уравнений в эквивалентную систему.
