Линейная алгебра. Краткий конспект. Лекция 1. стр. 20

N1

Геометрические векторы. Линейные операции с векторами

Сначала вспомним известные из школьной программы определения и свойства геометрических векторов.

Определение. Геометрическим вектором называется направленный отрезок.

Обозначаем: , А — начало, B — конец вектора.

Геометрические векторы также обозначают одной буквой: 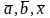и т.п.

Определение. Длина вектора — расстояние между точками A и B.

Обозначаем: и т.п.

Определение. Два вектора называются равными, если они коллинеарны (лежат на параллельных прямых), одинаково направлены и их длины равны.

Обозначаем: .

Определение. Два вектора называются противоположными, если они коллинеарны, равны по длине и противоположно направлены. Обозначаем: .

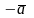Определение. Нулевым называется вектор, имеющий нулевую длину. Направление нулевого вектора не определено. Обозначаем: .

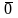Определение. Суммой векторов 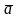и 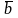называется вектор , определенный на рисунке (правило параллелограмма или правило треугольника). Обозначаем: .

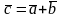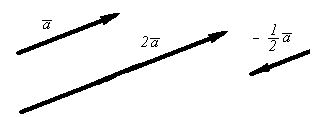
Определение. Произведением вектора на число 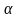называется вектор длины 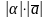, коллинеарный вектору , направление которого при 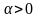совпадает с направлением вектора , а 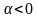— противоположно направлению вектора .

Определение. Ортом вектора называется вектор единичной длины, направление которого совпадает с направлением вектора .

Обозначаем: и т.п. Понятно, что .

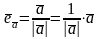Определение. Операции сложения векторов и умножение вектора на число называются линейными операциями с векторами.

Известно (нетрудно доказать), что для линейных операций с векторами справедливо:

1. ;

2. ;

3. ;

4. ;

5. ;

6. ;

7. ;

8. .

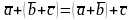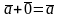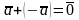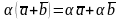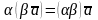Равенства 1-8 справедливы для произвольных векторов 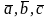и для любых чисел .

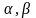N2

Углом между векторами считается тот из углов, который не превосходит . Если угол прямой, то векторы наз. ортогональными. Определение: Скалярным произведением двух векторов наз. число, равное произведению длин этих векторов на косинус угла между ними. Если хоть один из векторов нулевой, то угол не определен и скаляр­ное произведение по определению считают равным нулю.

Скалярное произведение векторов а и b обозначается (а,b). т.о., мы можем записать (а,b) = |a| |b| cos,

где ( – угол между векторами а и b. Очевидны следую­щие свойства операции скалярного умножения:

(1) Скалярное умножение коммутативно, т.е., для любых векторов а и b справедливо равенство (а,b) = (b,а). (2) (а,а) = |а|² для любого вектора а. (3) Скалярное произведение = 0 тогда и толь­ко тогда, когда сомножители ортогональны или хотя бы один из них = 0. (4) Векторы ортонормированного базиса удовлетворяют соотношениям (e₁,e₁) = (e₂,e₂) = (e₃,e₃) =1 Предложения: [1] Если базисные векторы e₁,е₂,е₃ ортогональны, то компоненты любого вектора а находятся по формулам: ₁ = (a,e₁)/|e₁|²; ₂ = (a,e₂)/|e₂|²; ₃ = (a,e₃)/|e₃|²; В частности, если базис ортонормированный, ₁ = (a,e₁); ₂ = (a,e₂); ₃ = (a,e₃);

[2] Для лю­бых векторов а,b,с и любых чисел  и b выполнено равенство (a+b,c) = (a,c) + (b,c). В частности, (а,с) = (а,c) и (a+b,c) = (a,с) + (b,с). Теорема 1. Если базис ортонормированный, то скалярное произведение векторов выражается через их компоненты по формуле (a,b) = ₁₁ + ₂₂ + ₃₃. Теорема позволяет написать выражение длины вектора через его компоненты в ортонормированном базисе: || = ₁²+₂²+₃² ***, а так же выражение угла между векторами через их компоненты в ортонормированном базисе:

И спользуя формулу ***, мы можем вычислить расстояние между точками, если заданы их координаты в декартовой системе координат. В самом деле, пусть точки А и В имеют соответственно координаты (x,y,z) и (x₁,y₁,z₁). Тогда расстояние между ними равно |AB| = (x₁–x)²+(y₂–y)²+(z₃–z)².

Векторное произведение:

Определение: Пусть даны векторы a и b. Построим по ним вектор с, удовлет­воряющий условиям: (1) |e| = |a| |b| sin  (sin0, т.к. 0), где  – угол между a и b;

(2) вектор с ортогонален векторам а и b; (3) векторы а, b, с образуют правую тройку векторов. Так построенный вектор с наз. векторным произ­ведением векторов а и b и обозначается [а, b]. Приведенные условия определяют векторное произведение с точностью до равенства, если сомножители – ненулевые векторы. Если хоть один из сомножителей – нуль, то векторное произведение по определению есть нулевой вектор. Из определения вытекает, что модуль векторного про­изведения неколлинеарных векторов численно равен пло­щади параллелограмма, построенного на сомножителях (если сомножители имеют общее начало). Векторное произведение равно нулю тогда и только тогда, когда сомножители коллинеарны (0-ой вектор коллинеарен любому вектору) Предложение: Векторное умножение антиком­мутативно, т.е., всегда [а,b] = – [b,а]. Действительно, из определения =>, что модуль векторного произведения не зависит от порядка сомно­жителей. Точно так же вектор [а, b] коллинеарен векто­ру [b, а]. Однако, переставляя сомножители, мы долиты изменить направление произведения, чтобы было выпол­нено условие (3) определения. Действительно, если a,b,[а,b] – правая тройка, то b,а,[а,b] – левая, а b, а, – [а, Ь] – снова правая тройка.

Смешанное произведение:

Определение: Число (а, [b,с]) наз. смешанным произведением векто­ров а,b,с и обозначается (а,b,с). Предложения: [1] Смешанное произведение неком­планарных векторов а,b и с по модулю равно объему па­раллелепипеда, построенного на сомножителях. Оно поло­жительно, если тройка а,b,с правая, и отрицательно, если она левая. Действительно, объем параллелепипеда, построенного на векторах а,b и с, равен (рис) произведению пло­щади основания |[b, с]| на высоту |a| |cos|. Здесь  – угол между векторами а и [b,с]. Поэтому мы можем записать V=|[b, c]| |a| |cos| = |(a,[b,с])| = |(а,b,с)|. [5] Смешанное произведение = 0 тогда и только тогда, когда сомножители компла­нарны (рис). Действительно, (а,b,с) = |a| |b,c| cos, где  – угол между векторами а и [b,с]. Равенство |a| |b,c| cos = 0 возможно только тогда, когда выполнено хоть одно из условий: а) |a| = 0. Очевидно, что тогда векторы компланарны; б) |[b, с]| = 0. Тогда b и с коллинеарны и, => а, b и с компланарны. в) cos = 0. Тогда вектор а ортогонален [b,с], т.е. компланарен b и с. Обратное утверждение доказывается аналогично: ес­ли а, b и с компланарны и не имеют места случаи а) и б), то имеет место случай в).

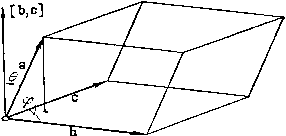
N3

Плоскость и прямая в пространстве:

Плоскость Р в декарто­вой прямоугольной системе координат Охуz может быть задана урав­нением одного из следующих видов: (1) Ax+By+Cz+D=0 – общее уравнение плоскости; (2) А(х–x₀)+В(у–y₀)+С(z–z₀) = 0 – уравнение плоскости, проходящей через точку M₀(x₀,y₀,z₀) перпендикулярно нормальному вектору п(А,В,C); (3) x/+y/b+z/c =1 – уравнение плоскости в отрезках, где ,b,с – величины направленных отрезков, отсекаемых плоскостью на коор­динатных осях Ox,Оу,Oz соответственно; (4) х cos+y cos+z cos =0 – нормальное уравнение пло­скости, где cos, cos, cos – направляющие косинусы нормального вектора п, направленного из начала координат в сторону плоскости, а p>0 – расстояние от начала координат до плоскости. Общее уравнение (1) приводится к нормальному виду (4) путем умножения на нормирующий множитель = –sgn D/A²+B²+C²

если плоскость Р задана нормальным уравнением вида (4), а M(x,y,z) – некоторая точка пространства, то выражение (М, P)=x cos+y cos+z cos–p задает отклонение точки М от плоскости Р, Знак (М, Р) ука­зывает на взаимное расположение точки М, плоскости Р и начала координат, а именно: если точка М и начало координат лежат по разные стороны от плоскости Р, то (М, Р)>0, а если М и начало координат находятся по одну сторону от плоскости Р, то (М, Р)<0. Расстояние (М, Р) от точки М до плоскости Р определяется равенством (М, Р) = |(М,Р) |. Прямая L в пространстве может быть задана:

[1] общими уравнениями

A₁x+B₁y+C₁z+D₁=0

A₂x+B₂y+C₂z+D₂=0, где коэффициенты A₁,B₁,C₁ не пропорциональны коэффициентам A₂, B₂, С₂, что равносильно её заданию как линии пересечения плоскостей; [2] параметрическими уравнениями

x=x₀+lt

y=y₀+mt

z=z₀+nt, или в векторной форме, где r₀(x₀,y₀,z₀) –радиус-вектор некоторой точки, принадлежащей прямой, a q(l,т,п) – направляющий вектор прямой; [3] каноническими уравнениями (x–x₀/l)=(y–y₀/m)=(z–z₀/n), что равносильно описанию прямой как линии пересечения трёх плоскостей, проецирующих эту прямую на координатные плоскости.

N4 Определителем n-го порядка (определителем квадратной матрицы n-го порядка n), n>1, называется число, равное сумме произведений элементов первой строки на их алгебраические дополнения:

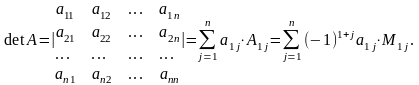
Справедливо следующее утверждение, которое мы не будем доказывать.

Теорема о вычислении определителя разложением по любой строке (столбцу). Определитель n-го порядка, n>1, равен сумме произведений элементов любой строки (столбца) на их алгебраические дополнения.

Пример. Вычислим определитель разложением по второй строке:

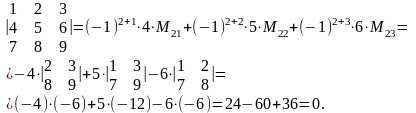
Следствие. Определитель треугольной матрицы равен произведению диагональных элементов. (Доказать самостоятельно).

Свойства определителей

Для определителей справедливы следующие утверждения — свойства определителей.

1. Определитель не изменяется при транспонировании: det A^T = det A.

2. При перестановке любых двух строк, определитель меняет знак.

3. Если в определителе есть две одинаковые строки, то он равен нулю.

4. Если все элементы строки определителя умножить на отличное от нуля число, то определитель умножается на это число: .

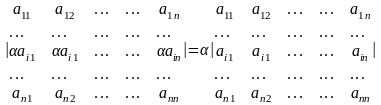5. Если в определителе есть две пропорциональные строки, то он равен нулю.

6. Определитель, содержащий нулевую строку, равен нулю.

7. Если квадратные матрицы A, B и С отличаются только i-й строкой и при этом i-я строка а матрицы С равна сумме соответственных элементов i-х строк матриц A и B, то detC=detA + detB:

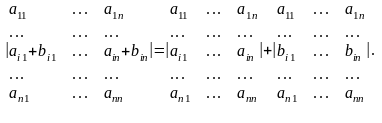
8. Определитель не изменится, если к элементам любой его строки прибавить элементы любой другой строки, умноженные на одно и то же число.

9. Сумма произведений элементов любой строки на алгебраические дополнения другой строки равна нулю: .

Поскольку определитель не меняется при транспонировании — утверждения 2—9 справедливы и для столбцов.

Перечисленные свойства позволяют упростить вычисление определителя.

Задачи: вычисление определителя 3-го порядка разложением по первой строке, определители треугольной и диагональной матриц, вычисление определителя приведением к треугольной форме, определители квадратной невырожденной матрицы и обратной к ней.

N5 Матрицы. Основные понятия. Виды матриц. Равенство матриц

Прямоугольная таблица m·n чисел, расположенных в m строках и n столбцах называется прямоугольной (m,n) матрицей или просто матрицей.

Некоторые часто встречающиеся виды матриц имеют собственные названия:

квадратная матрица, 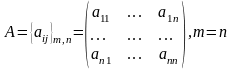, матрица, у которой одинаковое число строк и столбцов;

матрица-строка,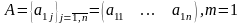 , матрица, у которой одна строка;

матрица-столбец, 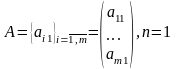, матрица, у которой один столбец;

диагональная матрица, 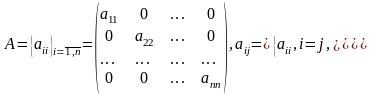квадратная матрица, у которой все внедиагональные элементы раны нулю;

единичная матрица, 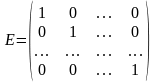диагональная матрица, у которой все диагональные элементы — единицы;

нулевая матрица, 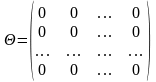, , матрица, все элементы которой — нули;

верхняя треугольная матрица, , квадратная матрица, у которой все элементы, расположенные ниже диагонали — нули;

нижняя треугольная матрица, , квадратная матрица, у которой все элементы, расположенные выше диагонали — нули.

Линейные операции с матрицами. Линейными операциями называются операции сложения и умножения на число.

Определение. Суммой двух матриц одинаковой размерности называется матрица той же размерности, каждый элемент которой равен сумме соответствующих элементов слагаемых: .

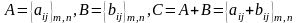Определение. Произведением матрицы на число называется матрица той же размерности, каждый элемент которой равен произведению соответствующего элемента на число: .

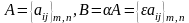Для операций сложения и умножения матрицы на число справедливо:

1. A+B = B+A,

2. A+(B+C) = (A+B)+C,

3. α(A+B) = αA+αB,

4. α(βA) = (αβ)A,

5. (α+β)A=αA+βA,

6. 1·A=A,

7. 0·A= .

Здесь A, B, C — произвольные матрицы одинаковой размерности, — нулевая матрица той же размерности (читается «тэта»), и — произвольные числа.

Умножение матриц

Операция умножения матрицы на матрицу определяется более сложным образом.

Определение. Пусть заданы две матрицы A и B, причем число столбцов из них равно числу строк второй. Если

то произведением матриц A и B называется матрица

, элементы которой вычисляются по формуле

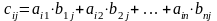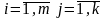, ; произведение матриц A и B обозначается AB: C=AB.

Итак, произведение двух матриц определено, если количество столбцов левого сомножителя равно количеству строк правого сомножителя.

Правило «строка на столбец». Произведение двух матриц имеет столько строк, сколько их у левого сомножителя и столько столбцов, сколько их у правого сомножителя.

Элемент произведения, расположенный в i–й строке и в j -м столбце равен сумме произведений

i -й строки левого сомножителя на соответственные элементы

j -го столбца правого сомножителя.