54 Основные понятия ортогональных сигналов. Скалярное произведение сигналов.
Ортогональные сигналы. Два сигнала называются ортогональными (orthogonal), если имеют нулевое скалярное произведение
u(t), v(t) = u(t)v(t) dt = 0.
Соответственно, два таких сигнала в своем функциональном пространстве являются взаимно перпендикулярными (угол между сигналами равен j = 90о), полностью независимыми друг от друга (некоррелированными, r = cos j = 0), и имеют нулевую энергию взаимодействия (Euv = 0).
Скалярное произведение произвольных сигналов u(t) и v(t) отражает степень их связи (сходства) по форме и положению в пространстве сигналов, и обозначается как u(t), v(t).
u(t), v(t) = ||u(t)||||v(t)|| cos , (2.1.4)
Физическую сущность скалярного произведения векторов в двумерном пространстве можно наглядно видеть на рис. 2.1.4. Это произведение "длины" (нормы) одного вектора на проекцию второго вектора по "направлению" первого вектора
55) Периодические сигналы. Ряды Фурье. Разложение сигналов в ряд-Фурье. Спектр сигнала.
Периодическим называется сигнал, повторяющийся через равные промежутки времени, - v(f) = V t + Т для всех значений t.
Наименьшая величина Т, удовлетворяющая этому равенству, называется периодом. Если поведение периодического сигнала на интервале Т известно, то известны его прошлое и будущее, поэтому периодический сигнал не может быть использован для передачи информации.
Интеграл от периодического сигнала является неопределенным или бесконечным, но среднее по времени существует:
V = Ит - Kt)dt. [1.2.1]
аоо -а
Усреднение по времени является общей операцией, применяемой как к периодическим, так и к непериодическим сигналам. Для периодических сигналов среднее за все время равно среднему за период:
J т/2
v=- lv{t)dt. [1.2.2]
-т/2
Средняя мощность сигнала определяется как величина V ;
сигнал конечной мощности удовлетворяет условию О < < оо .
Периодические сигналы являются сигналами конечной мощности. Их средняя мощность равна энергии за период, умноженной на число периодов в 1-й секунде, т. е. на частоту (/= 7/7.
Ряд Фурье
— представление произвольной функции f с периодом τ в виде ряда
Разложение в ряд Фурье
Л
юбой
сигнал можно представить в математической
форме во времени x(t) в виде разложения
в бесконечно тригонометрический ряд.
Каждое звено которого представляет из
себя гармонику с определенной частотой
и амплитудой. Давайте же поглядим на
разложение в ряд Фурье:
где, w = 2πf - круговая частота
- коэффициенты
Фурье.
Так же разложение в ряд Фурье часто записывают в комплексной форме (преобразование возможно с помощью формулы Эйлера):
,
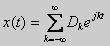где Dk - комплексные коэффициенты Фурье.
Вот мы и рассмотрели все основные формы представления ряда Фурье (комплексная, геометрическая).
Спектр сигнала
Спектр сигнала это распределение энергии сигнала по частотам. Спектр бывает амплитудный и фазовый. Если известна форма сигнала (зависимость от времени), спектр может быть рассчитан при помощи преобразования Фурье. Для периодического сигнала ряд Фурье, для непериодического -интегральное преобразование. Если есть какое-нибудь устройство или линия передач и известны его часотные характеристики, можно, задавая сигнал на входе, получить выходной сигнал. Для этого нужно получить спектр сигнала, затем рассмотреть, как на него воздействуют частотные характеристики устройства и тем самым получить спектр выходного сигнала. Затем обратным преобразованием Фурье получается сам выходной сигнал. Если совсем тупо - то вот есть сигнал, есть результат его Фурье-преобразования, и это и есть по определению спектр сигнала (какая доля всей мощности приходится на данную частоту или на данный диапазон частот)