51 Гост 19.701-90. Символы линий. Специальные символы.

3.3. Символы линий

3.3.1. Основной символ линий

3.3.1.1. Линия

Символ отображает поток данных или управления.

При необходимости или для повышения удобочитаемости могут быть добавлены стрелки-указатели.

3.3.2. Специфические символы линий

3.3.2.1. Передача управления

Символ отображает непосредственную передачу управления от одного процесса к другому, иногда с возможностью прямого возвращения к инициирующему процессу после того, как инициированный процесс завершит свои функции. Тип передачи управления должен быть назван внутри символа (например, запрос, вызов, событие).

3.3.2.2. Канал связи

Символ отображает передачу данных по каналу связи.

3.3.2.3. Пунктирная линия

Символ отображает альтернативную связь между двумя или более символами. Кроме того, символ используют для обведения аннотированного участка.

3.4. Специальные символы

3.4.1. Соединитель

Символ отображает выход в часть схемы и вход из другой части этой схемы и используется для обрыва линии и продолжения ее в другом месте. Соответствующие символы-соединители должны содержать одно и то же уникальное обозначение.

3.4.2. Терминатор

Символ отображает выход во внешнюю среду и вход из внешней среды (начало или конец схемы программы, внешнее использование и источник или пункт назначения данных).

3.4.3. Комментарий

Символ используют для добавления описательных комментариев или пояснительных записей в целях объяснения или примечаний. Пунктирные линии в символе комментария связаны с соответствующим символом или могут обводить группу символов. Текст комментариев или примечаний должен быть помещен около ограничивающей фигуры.

.

52 Радиотехнические сигналы. Детерминированные и случайные сигналы. Видоимпульсы и радиоимпульсы. Дискретные сигналы.

Традиционно радиотехническими сигналами принято считать любые электрические сигналы, относящиеся к радиодиапазону. С математической точки зрения, всякий радиотехнический сигнал можно представить некоторой функцией времени u(t), которая характеризует изменение его мгновенных значений напряжения (чаще всего), тока или мощности. По математическому представлению все многообразие радиотехнических сигналов принято делить на две основные группы: детерминированные (регулярные) и случайные сигналы.

Детерминированными называют радиотехнические сигналы, мгновенные значения которых в любой момент времени достоверно известны, т. е., предсказуемы с вероятностью, равной единице /1/. Примером детерминированного радиотехнического сигнала может служить гармоническое колебание. Следует отметить, что по сути дела детерминированный сигнал не несет в себе никакой информации и практически все его параметры можно передать по каналу радиосвязи одним или несколькими кодовыми значениями. Другими словами, детерминированные сигналы (сообщения) по существу не содержат в себе информации, и нет смысла их передавать.

Случайные сигналы – это сигналы, мгновенные значения которых в любые моменты времени не известны и не могут быть предсказаны с вероятностью, равной единице /1/. Практически все реальные случайные сигналы или большинство из них, представляют собой хаотические функции времени.

Видеосигнал представляет собой функцию самого полезного сигнала (обычно низкочастотный)

А радиосигнал - это (обычно) высокочастотная несущая, модулированная полезным сигналом.

Дискретный сигнал - сигнал, имеющий конечное число значений. Обычно сигналы, передаваемые через дискретные каналы, имеют два или три значения. Использование сигналов с тремя значениями обеспечивает синхронизацию передачи.

54)Ортогональные сигналы. Два сигнала называются ортогональными (orthogonal), если имеют нулевое скалярное произведение

u(t), v(t) = u(t)v(t) dt = 0.

Соответственно, два таких сигнала в своем функциональном пространстве являются взаимно перпендикулярными (угол между сигналами равен  = 90^о), полностью независимыми друг от друга (некоррелированными, r = cos , и имеют нулевую энергию взаимодействия (E_uv = 0).

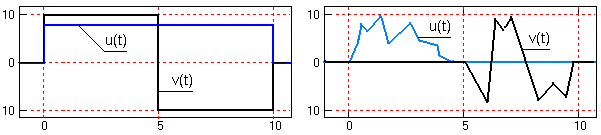
Рис. 2.3.1. Ортогональные сигналы.

На рисунке 2.3.1 приведены примеры взаимно ортогональных сигналов. Нулевое скалярное произведение двух левых сигналов обеспечивается их формой (равна нулю сумма положительных и отрицательных значений произведения сигналов), а двух правых - взаимным расположением (ненулевые значения сигналов не имеют общих координат).

Попутно заметим, что энергия и мощность суммы ортогональных сигналов обладают свойством аддитивности, т.к. имеют нулевое значение скалярного произведения и, соответственно, нулевую энергию взаимодействия.

Скалярное произведение произвольных сигналов u(t) и v(t) отражает степень их связи (сходства) по форме и положению в пространстве сигналов, и обозначается как u(t), v(t).

u(t), v(t) = ||u(t)||||v(t)|| cos , (2.1.4)

Физическую сущность скалярного произведения векторов в двумерном пространстве можно наглядно видеть на рис. 2.1.4. Это произведение "длины" (нормы) одного вектора на проекцию второго вектора по "направлению" первого вектора.

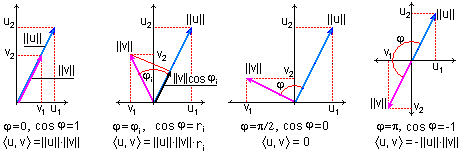
Рис. 2.1.4. Скалярное произведение сигналов в двумерном пространстве.

При кажущейся абстрактности скалярного произведения сигналов оно может приобретать вполне конкретный физический смысл для физических процессов, которые отображаются этими сигналами. Так, например, если v = F – сила, приложенная к телу, а u = s – перемещение тела под действием этой силы, то скалярное произведение W = F·s определяет выполненную работу, при условии совпадения силы с направлением перемещения. В противном случае, при наличии угла  между векторами силы и перемещения, работа будет определяться проекцией силы в направлении перемещения, т.е. W = s·F·cos .

Вычисление скалярного произведения обычно производится непосредственно по сигнальным функциям. Поясним это на примере двумерных сигналов с использованием рисунка 2.1.2. Для квадрата метрики сигналов s и v имеем:

||s-v||² = ||s||² + ||v||² – 2 ||s|| ||v|| cos ||s||² + ||v||² – 2s, v.

2s,v = ||s||² + ||v||² - ||s-v||² = (s₁²+s₂²)+(v₁²+v₂²)–{(s₁-v₁)²+(s₂-v₂)²} = 2(s₁v₁+s₂v₂).

s,v = s₁v₁+s₂v₂.

Обобщая полученное выражение на аналоговые сигналы:

s(t), v(t) = s(t)v(t) dt. (2.1.5)

Соответственно, для дискретных сигналов в N-мерном пространстве:

s_n, v_n = s_n v_n. (2.1.5')

Линейное пространство аналоговых сигналов с таким скалярным произведением называется гильбертовым пространством Н (второе распространенное обозначение - L2). Линейное пространство дискретных и цифровых сигналов - пространством Евклида (обозначение пространства - R2). Норма и метрика пространств Гильберта и Эвклида определяются выражениями (2.1.2) и (2.1.3). Метрика пространств называется среднеквадратичной метрикой и определяет среднеквадратичное отклонение одного сигнала от другого. В этих пространствах справедливо фундаментальное неравенство Коши-Буняковского

|s,v|  ||s||||v||, (2.1.6)

т.к. модуль косинуса в (2.1.4) может быть только равным или меньше 1

Для комплексного гильбертова пространства скалярное произведение вычисляется по формуле

s(t), v(t) = s(t)v*(t) dt. (2.1.7)

При определении функций в пространстве L²[a,b] вычисление скалярного произведения производится соответственно с пределами интегрирования от а до b.

Из выражения (2.1.4) следует косинус угла между сигналами:

cos  = s(t),v(t) /(||s||||v||). (2.1.8)

Физическое понятие "угла" между многомерными сигналами довольно абстрактно. Однако при рассмотрении выражения (2.1.8) совместно с выражением для квадрата метрики сигналов

^(s,v) = [s(t)-v(t)]² dt = ||s||² + ||v||² - 2||s||||v|| cos .

можно отметить следующие закономерности. При  (cos  = 1) сигналы "совпадают по направлению" и расстояние между ними минимально. При  = /2 (cos  = 0) сигналы "перпендикулярны друг другу" (иначе говоря – ортогональны), и проекции сигналов друг на друга равны 0. При  =  (cos  = -1) сигналы "противоположны по направлению" и расстояние между сигналами максимально. Фактор расстояния между сигналами играет существенную роль при их селекции в многоканальных системах.