Методические указания по выполнению и оформлению контрольной работы № 2

Контрольная работа выполняются по индивидуальным вариантам. Вариант соответствует последней цифре зачетной книжки студента, если последняя цифра 0, следует выполнять десятый вариант. Домашняя контрольная работа на проверку предоставляется за две недели до начала сессии. Однако этот срок являются крайним. Чтобы работа была своевременно прорецензирована, при необходимости доработана и сдана повторно, ее надлежит представить значительно раньше указанного срока.

Если в ходе написания работы у студента появляются вопросы или затруднения в решении задач контрольной работы, он может обратиться в филиал за консультацией. При выполнении контрольных работ необходимо соблюдать следующие правила:

1. В работу должны быть включены все задачи, указанные в задании, строго по своему варианту. Контрольные работы, содержащие не все задачи задания, а также содержащие задачи не своего варианта, не зачитываются.

2. Перед решением каждой задачи нужно привести полностью ее условие;

3. Задания следует решать в той последовательности, в какой они даны, строго соблюдая при этом нумерацию заданий;

4. Не допускается замена задач контрольной работы другими;

5. Решение заданий должно сопровождаться пояснениями; нужно привести в общем виде используемые формулы с объяснением используемых обозначений;

6. Работа может быть выполнена в школьной тетради, либо на листах формата А4;

7. Титульный лист оформляется в соответствии с приложением.

8. Если работа получила в целом положительную оценку (зачет), то студент допускается к экзамену. Если работа не зачтена, ее необходимо в соответствии с требованиями преподавателя частично или полностью переделать. Повторную работу надо выполнить в той же тетради (если есть место) или в новой тетради и вместе с не зачтенной работой сдать снова на проверку.

Задание 1

а) Исследовать на сходимость ряд:

Решение:

Несколько членов данного ряда не являются положительными. Если отбросить конечное число членов этого ряда, он станет положительным. Отбрасывание конечного числа членов ряда не влияет на сходимость и расходимость ряда, поэтому к этому ряду можно применить предельный признак сравнения. Если общий член ряда представляет собой отношение двух многочленов, то при подборе эталонного обобщенного гармонического ряда значение выбирают равным разности наибольший показателей степеней знаменателя и числителя. Наибольший показатель степени знаменателя равен 3, числителя – 1, поэтому =2, и в качестве эталонного ряда возьмем обобщенный гармонический ряд с членами . Найдем предел отношения общих членов исходного ряда и эталонного:

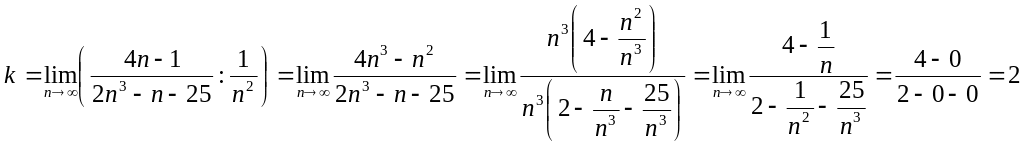
Поскольку предел конечен и отличен от нуля, то ряд исходный и эталонный либо оба сходятся, либо расходятся. Так как обобщенный гармонический ряд сходится, то исходный ряд на основании признака сравнения тоже сходится.

б) Исследовать на сходимость ряд:

Решение:

Найдем предел ; <1, значит, по признаку Коши данный ряд сходится.

в) Исследовать на сходимость ряд:

Решение:

Для исследования на сходимость данного ряда удобно применить признак Коши, поскольку , то . Так как <1, то ряд сходится.

Задание 2

а) Исследовать на сходимость знакочередующий ряд Если ряд сходится, то определить, сходится он абсолютно или условно.

Решение:

Это знакочередующийся ряд, для которого выполнены условия признака сходимости Лейбница: , и , поэтому ряд сходится. Он сходится условно, т.к. ряд, составленный из абсолютных значений, является гармоническим , который расходится.

б) Исследовать сходимость ряда .

Решение:

Рассмотрим ряд, составленный из абсолютных значений . Применим к нему признак сходимости Даламбера:

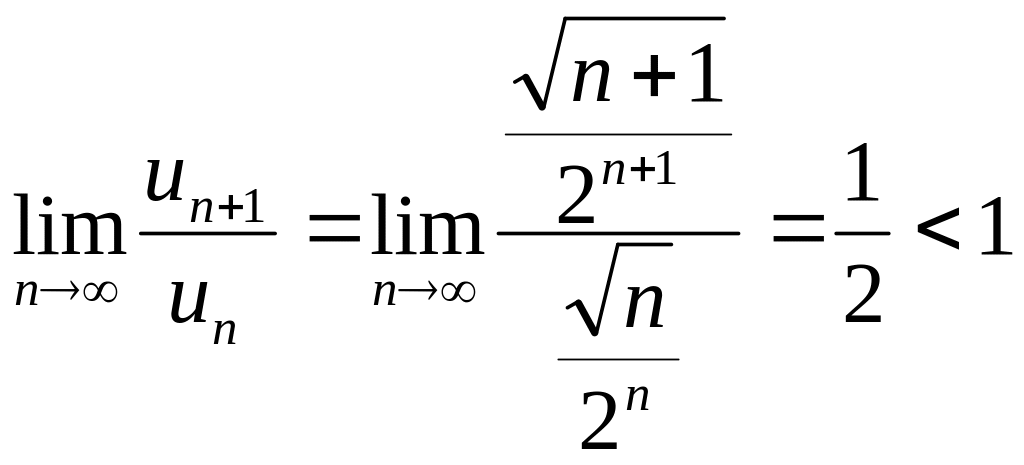, следовательно, этот ряд сходится, поэтому исходный ряд сходится абсолютно.

в) Исследовать сходимость знакочередующегося ряда:

Решение:

Вместо данного ряда возьмем ряд, составленный из абсолютных величин членов данного ряда . К данному ряду с положительными членами применим признак сравнения, сравним его с рядом , имеем .

Ряд - геометрическая прогрессия со знаменателем <1, значит, данный ряд сходится. По признаку сравнения исходный ряд абсолютно сходится.

г) Исследовать сходимость знакочередующегося ряда:

Решение:

Применим признак Лейбница. Так как ,

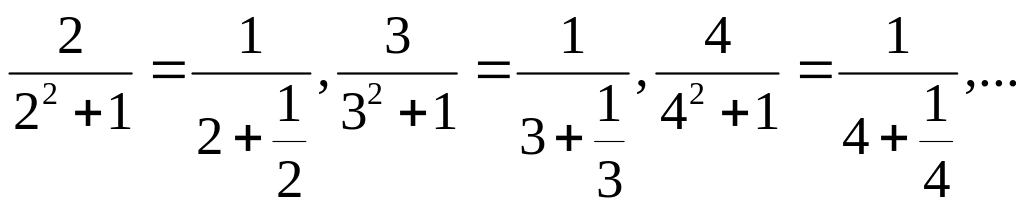то 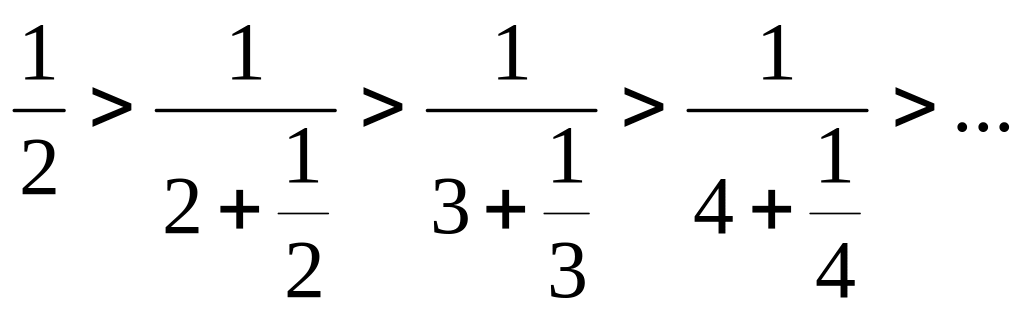Значит, выполнено первое условие признака Лейбница.

Найдем предел общего члена ряда: . Следовательно, второе условие признака Лейбница выполнено. Ряд сходится. Проверим данный ряд на абсолютную сходимость, рассмотрим ряд, составленный из абсолютных величин: . Ряд – гармонический, расходится. Значит, ряд по признаку сравнения тоже расходится. Делаем вывод, что ряд сходится условно.

Задание 3

В партии из 24 деталей пять бракованных. Из партии выбирают наугад 6 деталей. Найти вероятность того, что среди этих 6 деталей окажутся две бракованных (событие В).

Решение:

Шесть деталей из 24 можно выбрать способами.

Подсчитаем число исходов m, благоприятствующих событию В. Среди шести взятых наугад деталей должно быть две бракованных и четыре стандартных. Две бракованные детали из пяти можно выбрать способами, а четыре стандартных

детали из 19 стандартных деталей можно выбрать способами.

Каждая комбинация бракованных деталей может сочетаться с каждой комбинацией стандартных деталей, поэтому .

Найдем вероятность

Задание 4

На двух станках-автоматах производятся однотипные детали, причем производительность второго станка на 20% больше, чем производительность первого. Вероятность изготовления стандартной детали на первом станке равна 0,95, на втором станке – 0,94. Все изготовленные детали хранятся вместе на складе. Какова вероятность того, что наудачу взятая со склада деталь окажется стандартной? Какова вероятность того, что деталь изготовлена на первом станке, если при проверке она оказалась стандартной?

Решение:

Пусть событие А – деталь, взятая со склада стандартная. Гипотеза - деталь изготовлена на первом станке, гипотеза - деталь изготовлена на втором станке. По формуле полной вероятности , причем , . Вероятности гипотез находим из следующих рассуждений. Предполагая, что станки работают одновременно, и учитывая, что производительность второго на 20% больше производительности первого. Пусть на первом станке изготовлено х деталей, тогда на втором 1,2х деталей. Общее количество деталей на складе 2,2х, тогда ;

Вероятность события А будет равна , вероятность того, что стандартная деталь изготовлена на первом станке:

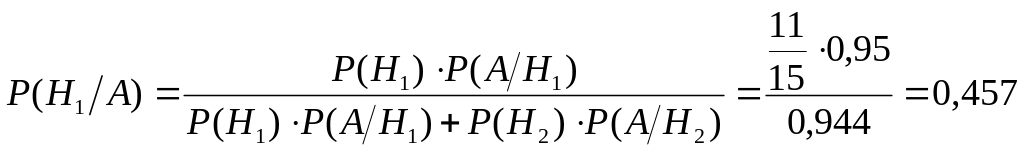
Задание 5

Найти сумму, разность, произведение и частное комплексных чисел и , результат записать в алгебраической, тригонометрической и показательной форме:

Решение:

Найдем сумму комплексных чисел: .

Найдем разность комплексных чисел: .

Найдем произведение комплексных чисел. Комплексные числа перемножаются как двучлены, причем заменяется на -1.

Найдем частное комплексных чисел. Для этого числитель и знаменатель дроби надо умножить на число, сопряженное знаменателю.

Представим число в тригонометрической и показательной форме. Модуль данного числа равен . Данное комплексное число находится в четвертой четверти комплексной плоскости, так как , поэтому . Следовательно . Запишем число в тригонометрической форме: .

Записываем число в показательной форме: . Аналогично записываются числа и в тригонометрической и показательной формах.

Задание 6

а) Вычислить:

Решение:

б) Вычислить:

Решение:

Перепишем данное комплексное число в виде: и представим его в тригонометрической форме. Модуль данного числа равен

, при вычислении аргумента учитываем, что и . Значит , отсюда

Задание 7

Решить графическим методом задачу:

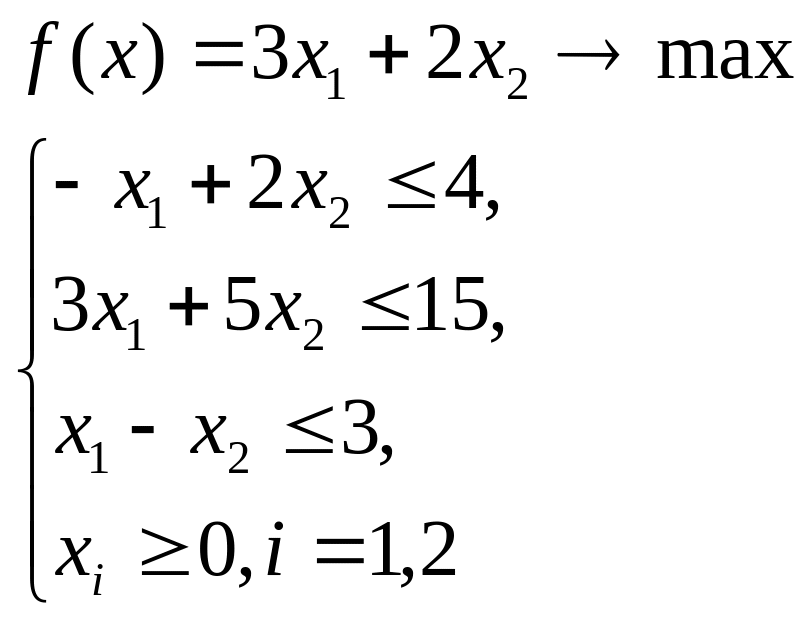
Решение:

Построим область допустимых решений, для этого построим графики линейных функций: , , .

Рассмотрим функцию . Если , то ; если , то .

Рассмотрим функцию . Если , то ; если , то .

Рассмотрим функцию . Если , то ; если , то .

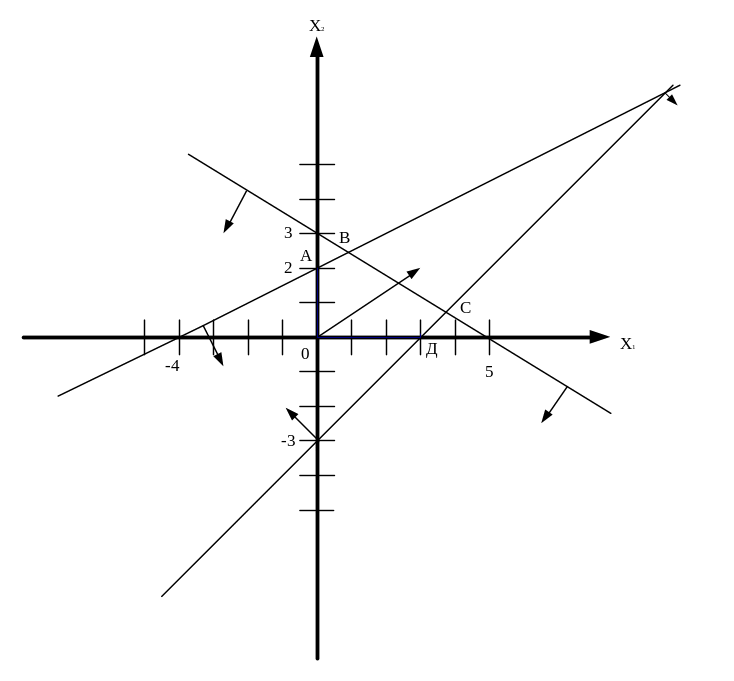
Область допустимых решений является непустым множеством, поэтому построим нормаль линий уровня, координаты вектора-нормали (3,2). Линию уровня следует переместить в направлении нормали, так как задача на максимум (в противоположном, если задача – на минимум). Последней точкой пересечения линии уровня и области допустимых решений будет точка В. Для того, чтобы найти координаты данной точки, необходимо решить систему линейных уравнений:

Умножая второе уравнение на (-3) и складывая с первым уравнением, получаем ,

Функция принимает максимальное значение при ,

Рисунок:

Задание 8

Решить симплексным методом задачу:

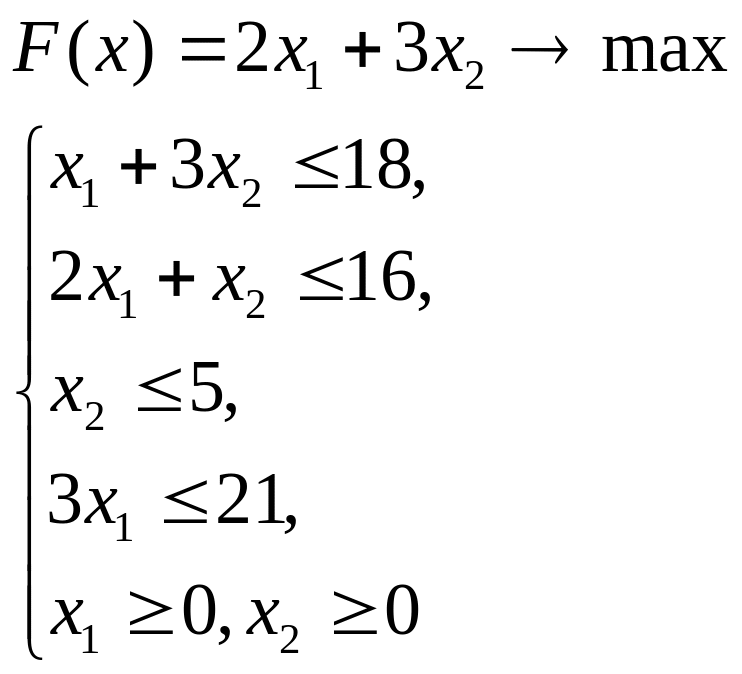
Решение:

Приведем данную задачу к каноническому виду:

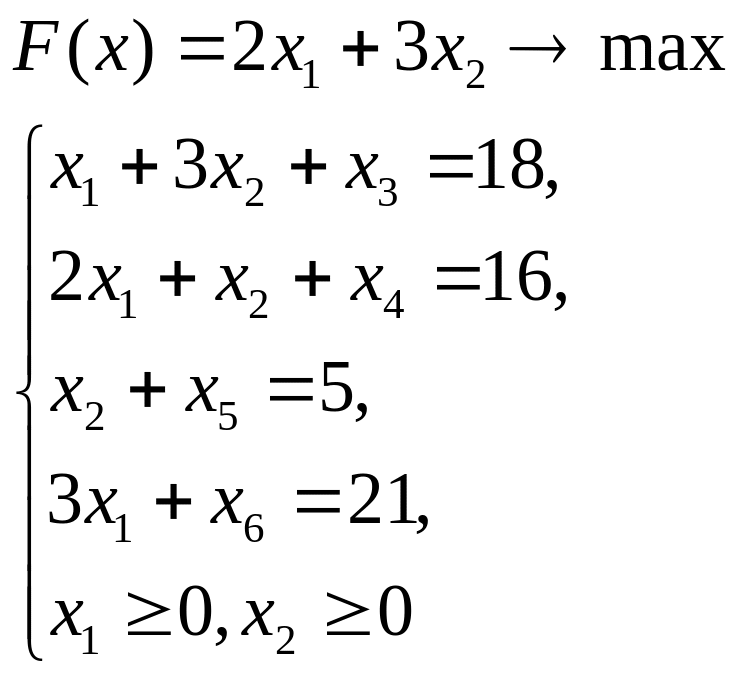
Составим первую симплексную таблицу:

Базис	Своб. члены	Переменные						Оценочные отношения
	18	1	3	1	0	0	0	18	6
	16	2	1	0	1	0	0	8	16
	5	0	1	0	0	1	0	-	5
	21	3	0	0	0	0	1	7	-
F	0	-2	-3	0	0	0	0

Минимальное оценочное отношение умножим на коэффициенты строки целевой функции и выбираем максимальное значение по абсолютной величине. Максимальным значением будет число 14 ( ). Столбец будет разрешающим, минимальное оценочное отношение для данного столбца равно 5, разрешающей строкой будет , разрешающим элементом будет число 1. С другими строками симплексной таблицы проведем жордановы преобразования и в разрешающей строке получаем все элементы, равные 0, кроме разрешающего. Для преобразования первой строки нужно разрешающую строку умножить на (-3) и прибавить к первой. Для преобразования второй строки нужно разрешающую строку умножить на (-1) и прибавить ко второй. Для преобразования строки целевой функции разрешающую строку умножаем на 3 и прибавляем к целевой. Рассмотрим после преобразований вторую симплексную таблицу:

Базис	Своб. члены	Переменные						Оценочные отношения
	3	1	0	1	0	-3	0	3
	11	2	0	0	1	-1	0	11/2
	5	0	1	0	0	1	0	-
	21	3	0	0	0	0	1	7
F	15	-2	0	0	0	3	0

Критерий оптимальности задачи на максимум не выполнен (в строке целевой функции есть отрицательные элементы), поэтому столбец является разрешающим. Минимальное оценочное отношение равно 3. Так как другие отрицательные элементы в строке целевой функции отсутствуют, то строка будет являться разрешающей, а элемент 1 – разрешающим. Относительно данного элемента проведем жордановы преобразования.

Для преобразования второй строки нужно разрешающую строку умножить на -2 и прибавить ко второй. Для преобразования четвертой строки нужно разрешающую строку умножить на (-3) и прибавить к первой. Для преобразования строки целевой функции нужно разрешающую строку умножить на 2 и прибавить к строке целевой функции. Третью строку мы не преобразовываем, так как в разрешающем столбце уже стоит значение 0. Получаем третью симплексную таблицу:

Базис	Своб. члены	Переменные						Оценочные отношения
	3	1	0	1	0	-3	0	-
	5	0	0	-2	1	5	0	1
	5	0	1	0	0	1	0	5
	12	0	0	-3	0	9	1	12/9
F	21	0	0	2	0	-3	0

Критерий оптимальности задачи на максимум не выполнен (в строке целевой функции есть отрицательные элементы), поэтому столбец является разрешающим. Минимальное оценочное отношение равно 1. Так как другие отрицательные элементы в строке целевой функции отсутствуют, то строка будет являться разрешающей, а элемент 5 – разрешающим. Разделим данную строку на 5 и относительно разрешающего элемента проведем жордановы преобразования.

Для преобразования первой строки необходимо разрешающую строку умножить на 3 и прибавить к первой. Для преобразования третьей строки необходимо разрешающую строку умножить на (-1) и прибавить к третьей. Для преобразования четвертой строки разрешающую строку умножаем на (-9) и прибавляем к четвертой. Для преобразования строки целевой функции нужно разрешающую строку умножить на 3 и прибавить к строке целевой функции. Получаем четвертую симплексную таблицу:

Базис	Своб. члены	Переменные						Оценочные отношения
	6	1	0	-1/5	3/5	0	0
	1	0	0	-2/5	1/5	1	0
	4	0	1	2/5	-1/5	0	0
	3	0	0	3/5	-9/5	0	1
F	24	0	0	4/5	3/5	0	0

Критерий оптимальности задачи на максимум выполнен (в строке целевой функции отсутствуют отрицательные элементы), отсюда максимальное значение функции равно 24 при и .