
- •34. Динамическая нагруженность привода станка при пуске для эквивалентной трехмассовой системы [5,9].
- •35. Нагрузка на вал двухмассовой системы при пуске, максимальные значения коэффициента динамичности, нагрузка на вал при любых законах нагружения [5].
- •37. Вычисление частот собственных колебаний трехмассовой системы [5,9,3].
- •38. Понятие о нормальных формах колебаний [5].
- •44. Частотная (комплексная передаточная) функция, формулы амплитуди и фазы частотной характеристики.
- •45. Частотные характеристики линейных элементов системы и построение афчх, ачх и фчх.
- •47. Методика операторной формы записи дифференциальных уравнений и их решение методом операционного исчисления
- •47. Методика операторной формы записи дифференциальных уравнений и их решение методом операционного исчисления
- •48. Характерные особенности приводов станков в зависимости от их типов
- •54. Характеристики и передаточная функция дифференцирующего дз
- •55. Характеристики и передаточная функция интегрирующего дз
- •56. Характеристики и передаточная функция колебательного дз
- •57, 58 Единичная ступенчатая и переходная функции, Единичная импульсная ( -функция) и импульсная переходная функции. Связь -функции с единичной ступенчетой.
- •59. Связь между переходной и импульсной переходной функциями.
- •60. Связь переходной и передаточной функциями и обратно.
- •65. 2. Принявобозначение принимаем в виде
- •70. Логарифмические частотные характеристики лачх и лфчх.
- •78.Цифровые вычислительные устройства в контуре управления
- •79.Решетчатые функции и z-преобразование решетчатой функции
- •80. Дискретная передаточная функция дискретного динамического звена
- •81. Дискретная передаточная функция замкнутой системы с цифровой вычислительной машиной в контуре управления:
- •82. Устойчивость дискретных замкнутых систем автоматического управления
- •83. Динамический расчет шпиндельного узла методом начальных параметров
- •86. Способы улучшения характеристик упругих систем станков
- •87. Способы уменьшения потерь на трение, повышения плавности перемещения и позиционирования подвижных узлов.
59. Связь между переходной и импульсной переходной функциями.



60. Связь переходной и передаточной функциями и обратно.
Передаточная функция — один из способов математического описания динамической системы. Используется в основном в теории управления, связи, цифровой обработке сигналов. Представляет собой дифференциальный оператор, выражающий связь между входом и выходом линейной стационарной системы. Зная входной сигнал системы и передаточную функцию, можно восстановить выходной сигнал.
В теории управления передаточная функция непрерывной системы представляет собой отношение преобразования Лапласа выходного сигнала к преобразованию Лапласа входного сигнала при нулевых начальных условиях.





63.
Пусть теперь f(t) непериодическая функция
и пусть при
 ,
f(t)
стремится к нулю, а интеграл
,
f(t)
стремится к нулю, а интеграл
 имеет конечное значение. Тогда функцию
f(t) нельзя представить в виде разложения
в ряд Фурье по ф.(39) или (45). Однако f(t)
можно представить простым выражением
ряда f(t) при бесконечном возрастании
периода T, или при
имеет конечное значение. Тогда функцию
f(t) нельзя представить в виде разложения
в ряд Фурье по ф.(39) или (45). Однако f(t)
можно представить простым выражением
ряда f(t) при бесконечном возрастании
периода T, или при
 .
Тогда при
.
Тогда при разность частот будет равнятся
разность частот будет равнятся
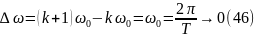
Найдем предельное выражение ряда Фурье f(t). Так как функция f(t) известна, то коефициенты ряда можно найти по ф.(43). Если выполнять интегрирование (43) при известной функции f(t), то получим

Учитывая ф.(47) можно записать в виде:

Обозначив
 и переходя к пределу ф.(48), получим:
и переходя к пределу ф.(48), получим:

Формула
(49) представляет интеграл Фурье, где
F(jω) - коефициетная функция, так как
выполняет ролькоефициентов обычного
родаФурье и может быть выражена через
f(t). Действительна при

64.
Формула (49) представляет интеграл Фурье, где F(jω) - коефициетная функция, так как выполняет ролькоефициентов обычного родаФурье и может быть выражена через f(t). Действительна при

Подставив
значение
 ф.(43), получим:
ф.(43), получим:

или (51)
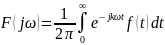
Формула (51) называется интегралом Лапласа. Интеграл Фурье и интеграл Лапласа являются двумя взаемно обратными преобразователями, тоесть первое является решением второго и наоборот. Интеграл Фурье и Лапласа можно обьеденить в одно уравнение
 -
прямое преобразование Лапласа
-
прямое преобразование Лапласа
 -
обратное преобразование Лапласа
-
обратное преобразование Лапласа
Для практическаго решения задач пользуемся более удобным

Это уравнение называют двойным интегралом Фурье.
Представление
f(t) двойным интегралом Фурье получим
при условии

Если это уравнение не выполняемо, то чтобы применить (52), необходимо предварительно умножить f(t) на функцию
 и
прибольшойвеличине
и
прибольшойвеличине можно считать, что
можно считать, что

Так как его условия выполняются представим его двойным интегралом
65. 2. Принявобозначение принимаем в виде
 .
.
Второй интеграл представляет собой интеграл Лапласа – Карсона
 ,
,
где - преобразованиеЛапласа-Карсона для
оригинала
- преобразованиеЛапласа-Карсона для
оригинала
Учитывая,
чтоSo-постоянное
число, tне
зависит от p,
функция
 может
бать винесена за знак інтеграла, по
этому
может
бать винесена за знак інтеграла, по
этому ,
эта формула называетьсяинтеграломБромвича,
которыйиспользуеться для
нахожденияоригиналаf(t)
по его изображению F(p),
выражение
,
эта формула называетьсяинтеграломБромвича,
которыйиспользуеться для
нахожденияоригиналаf(t)
по его изображению F(p),
выражение называетьсяфи-функцией,
котораяпозволяетзаписатьинтегралБромвича
в другойформе:
называетьсяфи-функцией,
котораяпозволяетзаписатьинтегралБромвича
в другойформе:
 .
.
Следовательнонахождениефункцииf(t)
или оригинала вычисленной переменной
t
сводиться к интегрированию фи-функции
 по комплекснойпеременной р с
постояннойвещественнойчастногоSo
и переменной частного
по комплекснойпеременной р с
постояннойвещественнойчастногоSo
и переменной частного
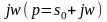 ,
изменяющейся от
,
изменяющейся от
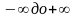 .
Интегрированиекомплекснойпеременнойимеетсвоиособенности.
.
Интегрированиекомплекснойпеременнойимеетсвоиособенности.
Таким образом для нахожденияизображенияданнойфункциииспользуетьсяпрямоепреобразованиеЛапласа-Карсона:
 .
.
В
результатеполучаеться система
алгебраическихуравнений,
котораярешаетьсяотносительноизображений,
являющихся функціями комплексного
переменного .
.
По средстваминтегралаБромвича, чтохарактеризуетобщий подход, делаетьсяобратныйподход от изображения к оригиналу:
 -
иначе это обратное преобразование
Лапласа.
-
иначе это обратное преобразование
Лапласа.
1.
Найдём выражение оригинала того же
использования изображения
 и
и ,
используяобщий поход
обратногопреобразованияпосредстваминтегралаБронвича:
,
используяобщий поход
обратногопреобразованияпосредстваминтегралаБронвича:
Имеем:

Интеграл Бромвича:
.
66.Рассмотрим в частности теорему свертывания (теорему Бореля). Полагаем, что изображение F(p) представлено в виде произведения изображений:
 .
.
Используем прямое преобразование Лапласа:
 .
.
Для получим:
 ,
,
 .
.
Для дальнейшего изображения формулы используем свойства запаздывания (теорема смягчения).
 .
.
Где
функция
 называется
запаздывающей относительно функции
называется
запаздывающей относительно функции
на
отрезок
 ,
показано на рисунке:
,
показано на рисунке:

Рис. 8 – Схема смещения функции f(t) на .
Это свойство получается непосредственно на преобразовании Лапласа:
,
 .
.
Подставим оригинал изображенияF(p):
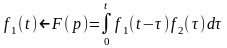 .
.
Так как функции и равноценны, то выполняяпреобразованиядля аналогичнополучимтеоремусвертки:
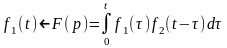 .
.
Оценка динамического привода
Устойчивость замкнутых систем регулирования являеться необходимым, но не достаточным условием практической пригодности системы. Иначе система должна удовлетворять некоторым критериям качества, важнейшим из которых является запас устойчивости и быстородействие.
Запас устойчивости линейной системы показывает как далеко от границ устойчивости находиться система. Бысродействие системы оценивается длительностью затухания переходного процесса.
Запас устойчивости и быстродействие можно оценить по виду переходной функции которая характеризует переходной процесс на выходе системы при подаче на ее вход единичной ступенчатой функции 1(t). Согласно рисунку запас устойчивостиоцениваетьсявеличинойрегулированя в %.

Рис.9 – Характеристика запасаустойчивости и быстродействия системы при оценке по переходной функции h(t).
 .
.
где -
максимальное
значение переходной функции.
-
максимальное
значение переходной функции.
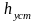 -
установившееся значение переходной
функции на выходе системы.
-
установившееся значение переходной
функции на выходе системы.
Запас устойчивости считается достаточным, если величина регулирования е больше 50%.
Быстродействие системы оценивается длительностью переходимого процесса tn, которое отсчитывается от момента подачи на вход системы единичной ступенчатой функции 1(t) до момента, корда выполняетьсянеравенство:
 .
.
Использования метода округления запаса устойчивости и быстродействия без трудоемкого построения кривой переходного процесса упрощает исследования переходных процессов.
68. В частности, запас устойчивости можно характеризовать расстоянием α в плоскости корней от мнимости до ближайшего к ней корня характерического уравнения, которое называется степенью устойчивости. Степень устойчивости считается апериодической, если ближайший корень к мнимой оси вещественный, и колебательный, если этот корень комплексный.
Время
перехода процесса связанное величиной
системы устойчивости отношением:
 .
.
Нахождение корней характерического уравнения для дифференциальных уравнений систем регулирования высокого порядка является сложной задачей, по этому для определения запаса устойчивости и быстодействия используют эксперементальнополученую характеристику.
Принимая
АЧХ замкнутой системы автоматического
регулирования имея ярко выраженный
резонансный пик, рис.10. При этом для
систем находящихся на границе устойчивости
 .
Что бы рабочая зона системы была удалена
от границ области устойчивости пик АЧХ
должен быть ограничен.
.
Что бы рабочая зона системы была удалена
от границ области устойчивости пик АЧХ
должен быть ограничен.

Рис.10 АЧХ замкнутой системы.
Запас устойчивости можно оценивать и показателю колебательности:
 .
.
Если
 ,
то запас устойчивости считается
достаточным. Время затухания переходного
процесса можно оценивать и по эмпирической
зависимости:
,
то запас устойчивости считается
достаточным. Время затухания переходного
процесса можно оценивать и по эмпирической
зависимости:
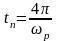 ,
где
,
где
 -
регулироваемая частота.
-
регулироваемая частота.
Оценку запаса устойчивости по АФЧХ разомкнутой системы оценивают по удаленности от точки -1 для систем с обратной отрицательной связью и от точки +1 для систем с положительной обратной связью.
Для
этой же цели вводят понятия запаса
устойчивости по амплитуде и по фазе.
Заштрихованая область АФЧХ считается
запретной для разомкнутой системы,
рис.11. Запас устойчивости по амплитуде
определяется положение точек а и b
и считается достаточным если
 ,
,
 .
Запас устойчивости по фазе определяется
углом α и считается достаточным, если
.
Запас устойчивости по фазе определяется
углом α и считается достаточным, если
 рад.
рад.
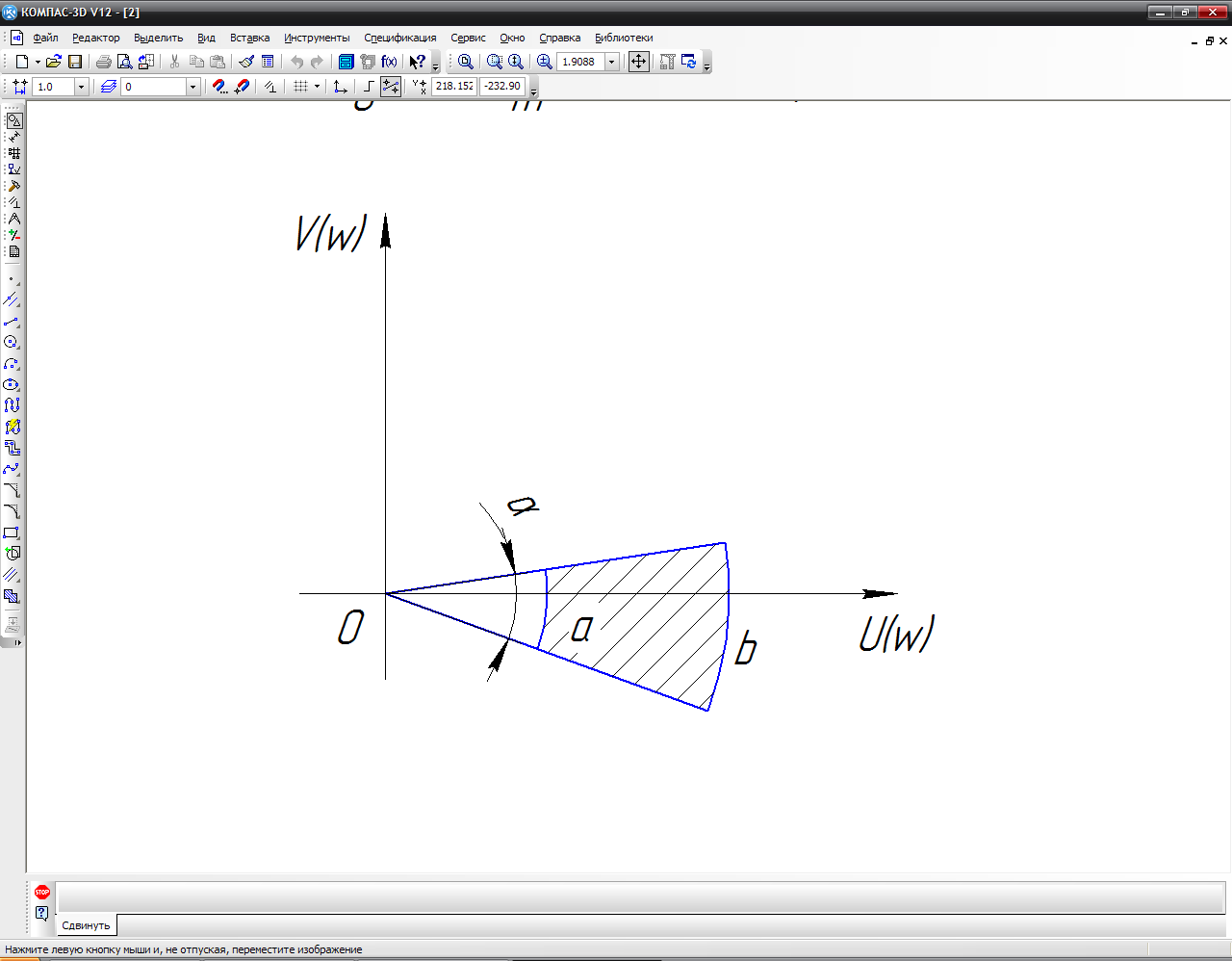
Рис.11. Запас устойчивости амплитуде и фазе посредством АФЧХ.
Построение графика переходной функции динамической системы.
Учитывая, что переходная функция связана с передаточной функцией обратно преобразованиям Лапласа:
 ,
для построенияеёграфикапредварительно
не обходимо определитьпередаточнуюфункцию
динамической системы. С целью упрощения
для построения графика кривой
переходногопроцесса и использующий
метод вещественныхтрапециодальных
характеристик, согласно котрому не
обходимо построитьграфиквещественной
части передаточнойфункциизамкнутойсистемы
в зависимости от изменениячастоты от
0 до ∞. Затемполученуюлиниюзаменяют
прямими из них составляемтрапеции таким
образом, чтобы при сложениивсех ординат
трапецииполучалсяисходнийграфикпереходнойфункции.
Каждаятрапецияимеет висоту Н, частоту
излома и частоту среза. Кроме того
трапецияимеет отдельные координаты
наклона
,
для построенияеёграфикапредварительно
не обходимо определитьпередаточнуюфункцию
динамической системы. С целью упрощения
для построения графика кривой
переходногопроцесса и использующий
метод вещественныхтрапециодальных
характеристик, согласно котрому не
обходимо построитьграфиквещественной
части передаточнойфункциизамкнутойсистемы
в зависимости от изменениячастоты от
0 до ∞. Затемполученуюлиниюзаменяют
прямими из них составляемтрапеции таким
образом, чтобы при сложениивсех ординат
трапецииполучалсяисходнийграфикпереходнойфункции.
Каждаятрапецияимеет висоту Н, частоту
излома и частоту среза. Кроме того
трапецияимеет отдельные координаты
наклона
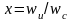 .
По
координатам
наклона трапеции для них находятcя
h-функции,
т.е.функция времени.
.
По
координатам
наклона трапеции для них находятcя
h-функции,
т.е.функция времени.
Таблица
h-функции
рассчитана для единичных трапеций, по
этому ординаты табличных значений,
соответствующих трапециям, необходимо
умножать на высоту соответствующей
трапеции. Масштаб времени необходимо
изменять в соответствующей функции
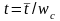 .
.
Просумировавпостроеныеграфикиполучаемисходнуюкривуюпереходногопроцесса.
Процедура построенийпереходнойкривойпроцесса методом трапеций приведена на рис.12, а все необходимыерасчеты сводяться в таблицу со столбцами w-частота, числитель и значение знаминателя P(w). При разбиении исходной кривой используем 4 трапеции.
X(0,5;0,8;0,77;0,58).

|
H |
wn |
wc |
x |
OABC |
117 |
100 |
130 |
0.77 |
OMNL |
-68 |
80 |
100 |
0.8 |
OEFK |
-20 |
40 |
80 |
0.5 |
ODPQ |
-16 |
150 |
260 |
0.58 |


Рис.12 Построение графика переходной функции:график вещественной части передаточной функции - а); эквивалентная замена графика трапециями –б); построение графика переходной функции – в).
Принципы,
на которые розбивается действительная
часть частотной характеристики рис.12
а) из условия, что сумма их ординат равна
ординате реальной кривой, определяеться
3 числами: частотой среза, высотой и
координатам наклона
,
где ,
, - соответственночастотыизлома и
срезакаждойиззаменяющихтрапеций.
- соответственночастотыизлома и
срезакаждойиззаменяющихтрапеций.
Затемнеобходимо
использовать таблицы h-функций,
которая оределяет собой кривую перехоного
процесса системы для реальной частотной
характеристики единичной трапеции с
параметрами H=+1
и
 .
Табличноезначениеh-функций
приводятся для различных значений
коэфициента наклона х, при этом для
значений х, которые между двумя табличными
значениями выполняеться интерполяция.
.
Табличноезначениеh-функций
приводятся для различных значений
коэфициента наклона х, при этом для
значений х, которые между двумя табличными
значениями выполняеться интерполяция.
Для
получения точек кривой переходного
процесса у(t)
на основании
полученых трапеций, необходимо перемножить
высоту трапеции Н на каждое значение
h-функций,
а время t
розделить на частоту среза: ,
гдеt
–табличное значение времени для
переходного процесса, частотная
характеристика которой единичная
трапеция.
,
гдеt
–табличное значение времени для
переходного процесса, частотная
характеристика которой единичная
трапеция.
Формула позволяет определить кривые переходного процесса, для каждой из состаляющих трапеций при единичном ступенчастом импульсе.
Кроме
метода трапеций для построения графика
переходного процесса может использоваться
вторая теорема Хевисайда, сгласно
которой изображение F(p)ордината
f(t)
представляет дробь:
 ,
гдеF1(p),
F2(p)
– полиномы
от р, соответствующие числителю
и знаменателю W(p).
,
гдеF1(p),
F2(p)
– полиномы
от р, соответствующие числителю
и знаменателю W(p).
Тогдаоригиналможнонайти по формуле:
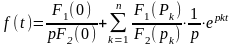 .
.
где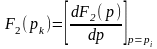 ;
;
 -
корни
характ.уравнения, соответствующего
знаменателя, среди которых нет кратных
корней.
-
корни
характ.уравнения, соответствующего
знаменателя, среди которых нет кратных
корней.
При заданной или найденной передаточной функции системы и действия её входа единичной ступенчастой функции 1(t), то переходная функция:
 .
.
Для
нахожденияоригиналаотизображения не обходимо найти корни
характерическогоуравненияизвыражения
.
Нахождениекорнейхарактерическогоуравнениявыполняется
методом делениямногочленов, используя
метод последовательных приближений. В
случаекомплексныхкорнейихудобнее
представить в показательнойформе, для
чегоопределяют модуль и аргумент
комплексного корня.
не обходимо найти корни
характерическогоуравненияизвыражения
.
Нахождениекорнейхарактерическогоуравнениявыполняется
методом делениямногочленов, используя
метод последовательных приближений. В
случаекомплексныхкорнейихудобнее
представить в показательнойформе, для
чегоопределяют модуль и аргумент
комплексного корня.
Подавляязначения
найдених корней и взяв приведеную от
знаменателя, выражение представляет
в показательнойформевида:
представляет
в показательнойформевида: ,
,
где
α-угол для сдвига фазы в градуса;
 корни
характерическогоуравнения.
корни
характерическогоуравнения.
Подставляянайдениезначения в формулу определяюторигиналыf(t) изображения переходной функции H(p), который соответствует переходноqфункции h(t). Задавая значение tпосредствам использования ЭВМ можно построить график переходной функции. Выполняя расчеты и построения позволяет проанализировать устойчивость процесс, его качественниехарактеристики (быстродействие, колебательность) . Если система сказывается неустойчивой, то делается корректировка параметров системы, уменшение коэффициентов передачи. Последний способ не всегда приемлем, так как уменшение коэффициентов передачи уменшает чувствительность системы и увеличивает ошибку.
