44. Частотная (комплексная передаточная) функция, формулы амплитуди и фазы частотной характеристики.

Амплитудно-частотная характеристика показывает, как пропускает звено сигнал различной частоты. Оценка пропускания делается по отношению амплитуд выходной и входной величин. Фазочастотиая характеристика показывает фазовые сдвиги, вносимые звеном па различных частотах, Как следует из сказанного выше, модуль частотной передаточной функции представляет собой четную функцию частоты, а фаза— нечетную функцию частоты.

Частотная передаточная функция звена есть изображение Фурье его функции веса, т. е. имеет место интегральное преобразование

Для реальной системы некоторые ее системные характеристики могут быть определены экспериментально. Для определения частотной передаточной характеристики на вход следует подавать гармонические колебания

и измерять амплитуду и фазу гармонического сигнала на выходе

При изменении частоты входного сигнала на выходе линейной цепи могут изменяться амплитуда и фаза. Частотной передаточной характеристикой цепи называется комплексная функция

Модуль этой функции K(w ) называется амплитудно-частотной характеристикой цепи, а разность фаз j вых - j вх =j к - фазо-частотной характеристикой цепи. Распространяя это определение и на область отрицательных частот, получают более обобщенную передаточную характеристику, которую обозначим через или , причем H(w )=K(w ), jн(w >0)=jk, jн(w <0)=-j k. Теоретически можно получить выражение для частотной передаточной характеристики, используя установившееся решение дифференциального уравнения, связывающего напряжения (или токи) на входе и выходе линейной системы. В общем виде это уравнение можно свести к одному дифференциальному уравнению вида

Амплитудно-частотная характеристика показывает, как пропускает звено сигнал различной частоты. Оценка пропускания делается по отношению амплитуд выходной и входной величин. Фазочастотная характеристика показывает фазовые сдвиги, вносимые звеном па различных частотах.

45. Частотные характеристики линейных элементов системы и построение афчх, ачх и фчх.

Исследование динамических процессов может выполнятся во временной и частотной областях. Исследование во временной области часто вызывает затруднения и поэтому для линейных систем широко используется частотный метод, который позволяет получить реакцию системы (элемента или динамического звена) на любой периодический сигнал.

П

(46)

усть на вход системы подан гармонический сигнал.

x(t)=x cos ωt.

п

(47)

(48)

о формуле Эйлера:

cos ωt= .

Тогда подставив (47) в формулу (46) получим:

x(t)= .

При установившемся режиме работы на выходе системы также получается гармонический сигнал, но сдвинутый по фазе относительно входного сигнала на угол Ψ(t), т.е.:

y(t)=Y(ω) cos .

П

(50)

(51)

одставив (48) и (49) в ф. (9) через дифференциальный оператор А(р)y(p)=B(p)X(p) и применив принцип суперпозиции, получим, заменив комплексное число на jω:

A(jω) y(ω) e^jΨ(ω)=B(jω)x

или

Формула (51) называется частотной или комплексной передаточной функцией, которая представляет комплексное число, модуль которого согласно записанного соотношения равен отношению амплитуд выходного сигнала к входному. Таким образом, частотная передаточная функция или частотная характеристика может быть получена из обычной передаточной функции простой заменой р на jω, т.е. р= jω. В свою очередь частотную передаточную функцию (51) можно представить в виде комплексного числа:

W

(52)

(jω)=

Тогда амплитуда частотной характеристики W(jω) найдется как модуль комплексного числа, согласно ф. (52), т.е.:

A

(53)

(ω)= ,

а фазовый сдвиг:

Ψ

(54)

(55)

(ω)=arctg .

Формулы (53) и (54) используют для построения частотных характеристик, которые дают наглядное представление частотных свойств элементов и системы в целом. Амплитудно – фазовая частотная характеристика (АФЧХ) строится на комплексной плоскости (u,v). Длинна вектора равная модулю частотной характеристики (его амплитуде) проводится из начала координат в точку АФЧХ, соответствующей какой – либо частоте, угол между этим вектором и вещественной осью Re отсчитывается против часовой стрелки и соответствует аргументу или фазе W(jω).

Возвращаясь к примеру упругой системы ф. (45) ее частотная характеристика будет:

W(jω)= ,

где W(jω) – имеет смысл динамической податливости

Выделим вещественную и мнимую часть ф. (55) для чего, домножив знаменатель на разность оснований, получим разность квадратов. Возведя j в квадрат и домножив числитель на тоже выражение окончательно получим:

W

(56)

(57)

(jω)= ,

где действительная часть и соответственно мнимая часть будут:

U_ω=Re=-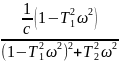 ; V_ω=I_m=- .

Задавшись различными частотами ω, находим для ее значения свой модуль и аргумент, как разность фаз по формулам:

A

(58)

= ; tgφ= ,

где А – модуль (амплитуда), а tgφ – фаза комплексного числа W(іω)

Предварительно остановимся на вопросе оценки динамической характеристики частотными методами. При анализе частотным методом необходимо выполнить переход от временной области к частной, который как уже отмечалось осуществляется посредством преобразований Лапласа, при котором исходное ДУ представляется в виде алгебраического S или в функции дифференциального оператора р= . Переход к частотной области достигается заменой оператора р на jω, где j - мнимая единица. Так если дифференциальное уравнение в матричной форме и его аналог имеют:

(59)

; ,

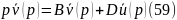т

(60)

о после перехода в частотную область, оно преобразуется к виду:

( jωI-B) ,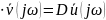

где I – единичная матрица, B, D – постоянные матрицы; - вектор приращения переменных состояния без воздействия возмущений (статическое состояние), - вектор переменных входных воздействий.

Решение уравнения (60) позволяет получить вектор (jω) для выбранного ряда частот. Построение АЧХ и ФЧХ сводится к нахождению модуля и аргумента этого вектора, представленного в комплексной форме (jω)= на заданных частотах ω при единичной амплитуде возмущения.

А нализ частотных характеристик во временной области, например, при подаче на вход гармонического сигнала требует больших затрат машинного времени и является более трудоемким по сравнению с частотным методом. Обычно временная характеристика рассматривает изменение во времени входной и выходной координат. Наличие таких характеристик для всего диапазона частот позволяет построить частотные характеристики: АЧХ, ФЧХ и АФЧХ, рис. 5. При этом амплитудно – частотная характеристика АЧХ характеризует положение амплитуд выходного А_вых к амплитуде входного А_вх сигналов т.е. А( ω)= . ФЧХ характеризует разность выходной и входной фаз этих сигналов в зависимости от частоты т.е.

а)

б)

в)

г)

Рис. 5. Временная -а), амплитудно – частотная характеристика (АЧХ) – б), фазо – частотная (ФЧХ) - в) и амплитудно – фазо –частотная (АФЧХ)- г) характеристики

А

ФЧХ совмещает обе характеристики АЧХ и ФЧХ и используется для оценки устойчивости системы. Данные для ее построения могут браться с временной, АЧХ и ФЧХ характеристик. АФЧХ является динамической характеристикой и представляет собой комплексную величину, построенную на комплексной плоскости с действительной Re и мнимой I_m осями, а также это частотная характеристика вида W(jω)= Re+i·I_m, которую можно представить в виде зависимости от амплитуды и сдвига фаз, т.е.:

W(jω_i)=A_i(cosφ_i+j sinφ_i), (i=1,2,…n).