55. Доказать локальную предельную теорему Муавра-Лапласа.

Локальная теорема Лапласа. Вероятность того, что в n независимых испытаниях, в каждом из которых вероятность появления события равна р(0<p<1), событие наступит ровно k раз (безразлично, в какой последовательности), приближенно равна (тем точнее, чем больше n). Pn(k)=1/(корень из npq)*фи(х). Здесь Фи(х)=1/(корень из 2пи)*е в степени –х*2/2, x=k – np/(корень из npq). Интегральная теорема Лапласа. Вероятность того, что в n независимых испытаниях, в каждом из которых вероятность появления события равна р(0<p<1), событие наступит не меньше k1 раз и не более k2 раз, приближенно равна: P(k1;k2)=Ф(х’’) – Ф(х’). Здесь Ф(х)=1/(корень из 2пи) * интеграл от0 до х е в степени –(z*2/2)dz – функция Лапласа, х’=(k1 – np)/(корень из npq), х’’=(k2 – np)/(корень из npq).

56. Доказать интегральную предельную теорему Муавра-Лапласа.

Пусть 0< p <1, тогда для схемы Бернулли при n  для любых a и b справедлива формула

.

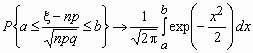Отсюда, в частности, следует, что для вычисления вероятности того, что число успехов в n испытаниях Бернулли заключено между k₁ и k₂, можно использовать формулу

,

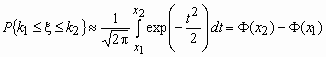где , , 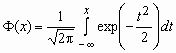- функция Лапласа.

Точность этой приближенной формулы растет с ростом n.

Если npq сравнительно невелико, то лучшее приближение дает формула

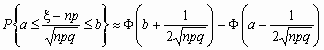
и для вычисления вероятности того, что число успехов в n испытаниях Бернулли заключено между k₁ и k₂, можно использовать формулу

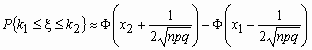, где , .

57. Доказать теорему Бернулли о сходимости относительной частоты появления события к вероятности этого события.

58. Доказать неравенство Чебышева.

Если случайная величина Х имеет математическое ожидание и дисперсию, то для любого

Докажем это неравенство для абсолютно непрерывной случайной величины. Для дискретных случайных величин доказательство проводится аналогично, только интегралы заменяются соответствующими суммами.

Обозначим МХ = а, имеем:

(1)

Область интегрирования можно записать в эквивалентной форме , поэтому в этой области ,(2)

Последний интеграл с неотрицательной подынтегральной функцией может только возрасти, если расширить область интегрирования до всей прямой:

(3)

Собирая последовательно равенство (1) и неравенства (2),(3), получаем неравенство Чебышева.

59. Доказать теорему Чебышева.

Если независимые случайные величины имеют математические ожидания и ограниченные в совокупности дисперсии , то разность средних арифметических случайных величин и средних их математических ожиданий сходится по вероятности к нулю:

В самом деле, применим неравенство Чебышева к случайной величине . Поскольку

то

Следовательно,

таким образом, действительно

60. Понятие генеральной совокупности, выборки из нее. Представление выборки в виде вариационного ряда. Определение вариационного ряда.

61. Эмпирическая функция распределения, ее свойства, способ построения по выборке.

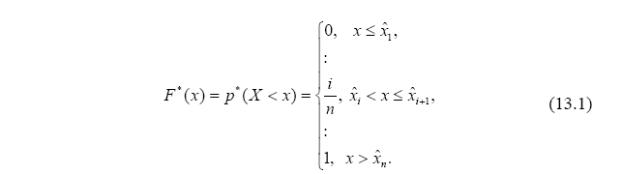
62. Понятие оценок числовой характеристики или параметра случайной величины. Свойства оценок.

оценкой числовой характеристики или параметра θ случайной величины называется функция от выборочных значений θ"с крышечкой" (х₁,…, х_n), которая в определенном смысле «близка» к истинному значению θ.

Качество оценки устанавливают проверяя, выполняются ли следующие свойства:

1 состоятельность

2 несмещенность

3 эффективность

63. Нахождение несмещенной оценки генеральной средней (математического ожидания) случайной величины.

64. Нахождение несмещенной и смещенной оценок генеральной дисперсии случайной величины.

для случайной выборки оценка дисперсии принимает вид:

1 _n

σ²"с крышечкой"=¯n¯ Σ(X_i - X¯)²

ⁱ⁼¹

раскрываем квадрат под знаком суммы в уравнении:

1 _n

Mσ²"с крышечкой"=¯n¯Σ(MX_i²-2M(X_iX¯)+MX¯²)

ⁱ⁼¹

находим теперь каждое из слагаемых в скобках под знаком суммы:

MX_i²=DX_i+( MX_i)²=σ²+а²

1 _n 1 _n σ²

M(X_iX¯)=M(X_i¯n¯ΣX_j)=¯n¯( MX_i²+Σ MX_i MX_j)=¯n¯+а²

^{j=1 i,j=1}

^{i не равно j}

1 _n 1 _n 1 _{n n} σ²

MX¯²=M(¯n¯Σ X_i*¯n¯Σ X_j)=¯n²¯(Σ MX_i²+Σ MX_i MX_j)=¯n¯+а²

^{i=1 j=1 i=1 i, j=1}

^{i не равно j}

подставим найденные выражения в формулу (она вторая по счету) и получим:

σ² n-1

Mσ²"с крышечкой"= σ²- ¯n¯= ¯n¯ σ²

Отсюда мы видим, что оценка σ²"с крышечкой" имеет систематическое смещение(-σ²/n),

Т.е. эта оценка занижает в среднем истинное значение дисперсии на σ²/n.

С целью устранения смещения скорректируем оценку следующим образом:

n 1 _n

s²=¯n-1¯* σ²"с крышечкой"=¯n-1¯Σ(X_i - X¯)²

ⁱ⁼¹

в самом деле:

n

M s²=¯n-1¯M σ²"с крышечкой"= σ²

Т.е. скорректированная оценка действительно не смещена.