§ 9.4 Программирование плис.

Для реализации функций на ПЛМ необходимо учитывать следующее:

Использовать ПЛМ минимальной сложности, для чего следует уменьшать число термов в заданных функциях их минимизацией.

Программирование ПЛИС производится с помощью специальных устройств – программаторов, в которые вводится информация о необходимости состояния перемычек.

Такую информацию удобно представлять таблицей истинности (программирования).

В таблице используются символы:

Н – переменная входит в прямом виде, следовательно перемычка остается на линии прямого входа, а на его инверсной линии она пережигается.

L – инверсная переменная входит в терм, перемычка сохраняется, а на прямой линии пережигается.

«–» - переменная не входит в терм. Обе перемычки на ее входе можно удалить, либо оставить.

При входах X· =0, конъюнктор на выходе будет иметь «0».

«А» - ставится в столбце функции и означает наличие связи конъюнктора И с выходом ПЛМ через дизъюнктор ИЛИ, следовательно перемычка должна сохраняться между выходом И и входом ИЛИ.

«–» в столбце функции означает отсутствие перемычки между выходом И и входом ИЛИ.

Последние два пункта обозначают программирование матрицы М2.

Пример программирования системы уравнений приведен на рис.9.08 а) и б).

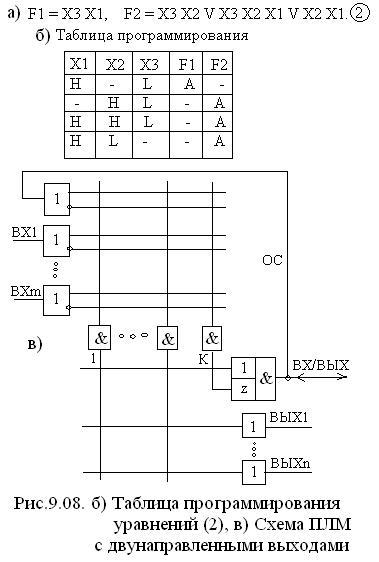
§ 9.5 Расширение функциональных возможностей плм и пмл.

На рис.9.08 в) приведена схема ПЛМ с двунаправленными выходами, которая имеет 4 режима работы, в зависимости от программирования конъюнктора К.

1. Все перемычки на входе конъюнктора К сохранены, на его выходе «0». Буфер Z в третьем состоянии, вход вых/вх работает как вход матрицы М1.

2. Все перемычки удалены, на выходе К – «1», буфер Z открыт, вывод вх/вых работает как выход М2 – n+1, но его сигнал не используется в матрице М1.

3. Выход с о.с. – сигнал вывода вх/вых используется в матрице М1.

4. При управлении буфером Z(вх/вых) – входы К программируются и при «1» на выходе К вывод вх/вых срабатывает как выход М2- n+1. В ПЛМ может быть несколько таких конъюнкторов К и выводов вх/вых, что позволяет менять соотношение числа входов m и выходов n.

Если входов m, выходов n и вх/вых p, то можно иметь:

число входов от m до m+p

число выходов от n до n+p,

При условии, что сумма числа входов и числа выходов не превышает число m+n+p.

На рис.9.09 а) и б) приведены примеры а) уравнения и б) схемы ПЛМ для воспроизведения функции F с использованием о.с.

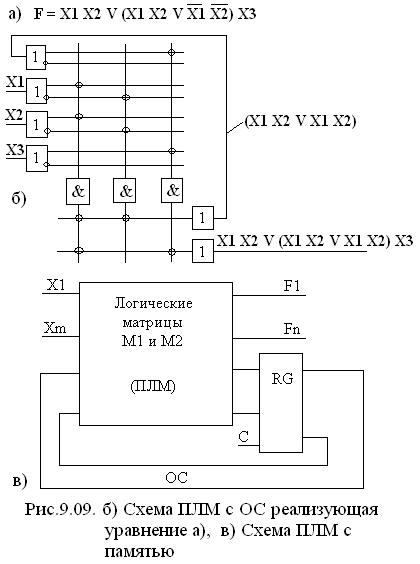
На рис. 9.09 в) приведена схема ПЛМ с памятью (в виде регистра RG), которая может реализовать автомат. Схема характеризуется четырьмя параметрами: m – число входов, n – число выходов, l – число термов, r – число элементов памяти (число разрядов RG).

Результат данного шага обработки информации зависит от результата предыдущего шага благодаря наличию о.с. с RG выходе ПЛМ. Максимальное число внутренних состояний автомата равно 2^r. Автомат синхронный, т.к. о.с. активируется по тактовому сигналу С.

На рис. 9.10 а) показана структура ПМЛ с разделяемыми конъюнкторами.

С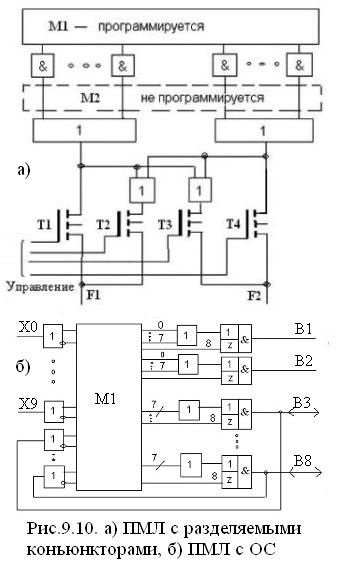 уть разделения: для двух смежных ИЛИ в ПМЛ отводится по несколько конъюгкторов и, благодаря наличию схем управления на транзисторах, часть конъюнкторов, не используемых простой функцией, например, F1, может быть переключена для использования более сложной функцией F2.

ПМЛ с обратными связями приведена на рис.9.10 б). Схема имеет 6 двунаправленных входов В3÷В8. Выходные буферы Z получают разрешение или запрещение передачи от матрицы М1.

В заключение можно отметить, что есть много микросхем (ПЛМ и ПМЛ) с более сложными логическими структурами на выходах, позволяющие реализовывать весьма широкий набор логических выражений. Приведем примеры комплексирования микросхем для увеличения числа их параметров.

На рис. 9.11 приведены:

а) – копмлексирование для увеличения числа n – выходов;

б) – для увеличения числа термов l;

в) – для увеличения числа входов m.