§ 5.3 Сумматоры с параллельным переносом.
Сумматоры с параллельным переносом не имеют последовательного распространения сигнала переноса от разряда к разряду. Во всех разрядах перенос формируется специальными схемами, на входы которых одновременно поступают все переменные, необходимые для его выработки.
Суть построения сумматора с параллельным переносом поясняет его структурная схема, показанная на рис. 5.5.
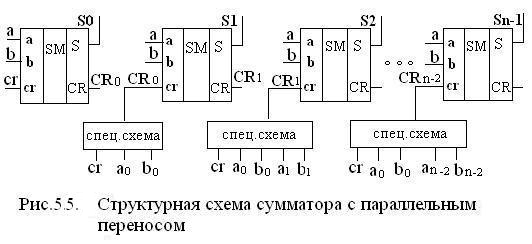
Основной задачей в таком сумматоре является построение специальной схемы для формирования сигнала переноса для каждого разряда.
Определим функции, реализуемые специальными схемами для разрядов.
Введем две вспомогательные функции (для удобства) рис. 5.6.
Функция генерации: γi=ai·bi, которая принимает единичное значение, если перенос на выходе данного разряда появляется независимо от наличия или отсутствия входного переноса.
Функция прозрачности (транзита): βi=ai
˅ ai
,
которая принимает единичное зачение
на выходе данного разряда появляется
только при наличии входного переноса.
Но поскольку при ai=bi=1
перенос формируется при γi=1,
то функцию транзита можно представить:
βi=ai
˅bi.
Теперь выражение для сигналов можно
представить так – CRi=γi˅βi·CRi-1,
на основе которого получены равенства
для разрядов 0,1 и 2.
На рис. 5.6 – представлены все неравенства.
На основе этих уравнений построены специальные схемы для сумматора трехразрядного для формирования переносов (рис. 5.7).
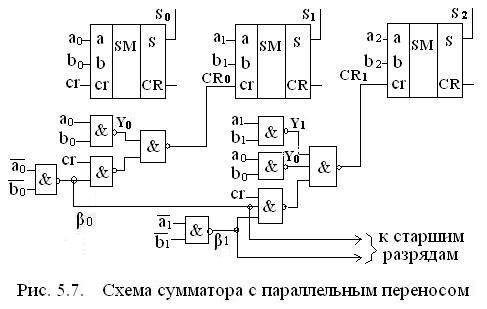
Из схемы видно, что время задержки суммирования складывается из:
- времени формирования функции βi раном τ,
- времени CR равном 3τ
- времени задержки одноразрядного сумматора SM равном (4÷5)τ.
Итого суммарная задержка составляет (7÷8)τ, причем она не зависит от числа разрядов. Фактически это не совсем точно, поскольку с ростом числа разрядов увеличивается нагрузка на элементы. Например, на элемент, формирующий β0 – подключен 1 элемент, β1 – подключаются 2 элемента и т. д. А это приводит к росту задержки τ этих элементов, и начиная с определенного числа разрядов, сумматор начинает терять преимущества параллельного переноса по быстродействию.
Практически используются:
-сумматоры до четырех разрядов – последовательный перенос,
-сумматоры до восьми разрядов – параллельный перенос.
§ 5.4 Двоично-десятичные сумматоры.
Для операций над десятичными числами каждая цифра от 0 до 9 представляется двоичной тетрадой, после чего операции над десятичными числами производятся над тетрадами, как над двоичными числами.
Такое представление десятичных чисел получило название двоично-десятичного кода, отнесенного к классу взвешенных кодов. Очевидно, что для представления десяти цифр необходим четырехразрядный двоичный код. На рис. 5.8 представлена таблица соответствия десятичных цифр двоичным тетрадам.
И
з
таблицы видно, что тетрады двоичного
кода, начиная с 1010 и до 1111 не используются
(будем считать их запрещенными),
следовательно при суммировании тетрад
с 0000 до 1001 в итоге могут появиться
запрещенные тетрады, что приведет к
неверному результату и подстверждает
пример суммирования, рассмотрены на
рис. 5.8, из которого видно, что тетрада
1110 запрещенная, оказалась с избытком
10 и потребовала коррекции – вычитания
этого избытка 10, представленного в доп.
коде и переноса 1 в следующую (старшую)
тетраду. На основе этих рассуждений
можно построить сумматор для подобных
сложений одноразрядных десятичных
чисел, представленных двоичными
тетрадами.
Такой сумматор. его УГО и наращивание его разрядности приведены на рис.5.9 а), б), и в) соответственно.
Из схемы видно, что если в результате суммирования получается разрешенная тетрада, то а выходе логической схемы формируются нули, и следовательно, разряды «bi» SM2 (2) влияния на разряды аi, поэтому результат суммирования в SM2(1) формируется без изменения.
Если же образуется запрещенная тетрада, логическая схема на ее основе сформирует коррекционную комбинацию и результат в SM2 (2) будет скорректирован.
При вычитании двоично-десятичных чисел используются преобразователи числа В (вычитаемого) в дополнение до 9 (получение обратного кода значения вычитаемой тетрады) на основе соотношения |W=9-B|, где W – дополнение, В – вычитаемое.
Фукционирование тактов преобразоветелей описывается таблицей дополнений, представленной на рис. 5.10 а), а соединение преобразователя с десятичным сумматором на рис. б).
где: SUB-(Substract) – вычитание ,SUB=0 – сложение, SUB=1 – вычитание, Z – сигнал установки нулевого значения на выходе блока. Z=0 – на выходах «0».