§ 9.2. Разновидность плм: ппзу.

Рассмотрим пример №1: построить преобразователь трехразрядного кода в двухразрядный на основе ПЛМ.

Составим таблицу соответствия трехразрядного кода двухразрядному. Таблица представлена на рис.9.05 а), в которой обозначены ti – термы,Fi – разряды двухразрядного кода. На основе этой таблицы составляются уравнения для получения значений разрядов Fi, приведенных на рис.9.05 б). Реализация уравнений показана на рис.9.05 в).

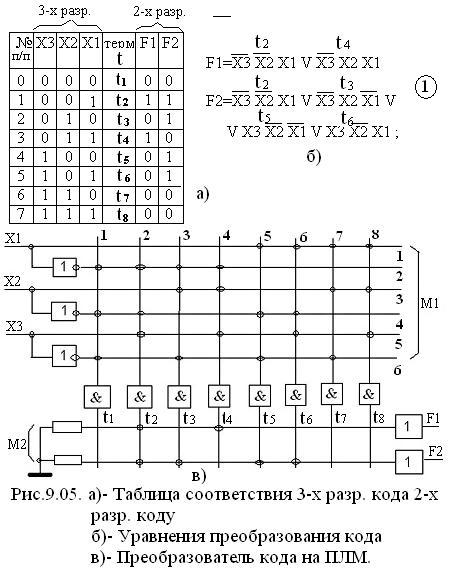
В функциональной схеме (рис. в) необходимы:

- трехвходовые И, четырехвходовые ИЛИ,

- оставленные перемычки, остальные ликвидированы.

В рассмотренном примере:

Матрица М1 – составная часть дешифратора (2³=8) DC, реализует все возможные конъюнкции ti трехразрядного кода. В примере использовано только 5: t2, t3, t4, t5, t6 за счет программирования М2 в соответствии с необходимостью получения кодовых комбинаций двухразрядного кода. Матрица М1 – не программировалась. М2 – неполный дешифратор на 2 выхода и 6 входов. Полученная схема реализует систему уравнений , имеет 24 элемента (перемычек) связи в М1 и 6 элементов(перемычек) связи в М2.

Схемы ПЛМ, в которых программируется только М2 получили название ППЗУ – программируемые постоянные запоминающие устройства.

Фактически ППЗУ являются частным случаем ПЛМ. УГО ППЗУ отличается от УГО ПЛМ только надписью ROM вместо RLM.

Пример №2. Построить тот же преобразователь кода (3^х разр. в 2^х разр.) на ПЛМ, применив программирование матриц М1 и М2.

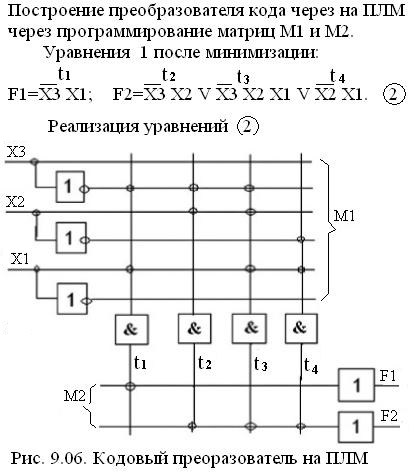
Используя систему уравнений , после их минимизации получим: (рис.9.06 )

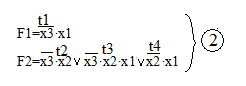
Реализация уравнений приведена на рис.9.06.

Здесь: 3 – двухвходовых И и 1 – трехвходовый И,

1 – одновходовый и 1 – трехвходовый ИЛИ.

Число используемых связей (перемычек) уменьшилось:

в М1 с 24 до 9, в М2 с 6 до 4.

Другими словами: ПЛМ про программировании М1 и М2 решает ту же задачу преобразования кода проще, чем ППЗУ.

Особенности ПЛМ по сравнению с ППЗ.

1. ППЗУ имеет полный дешифратор, в котором число термов 2^m, где m –разрядность входного кода, а в ПЛМ t<2^m.

2. Матрица М1 в ПЛМ тоже программируется.

3. Программирование матрицы М1 позволяет:

а) Возбуждать одни и те же вертикальные шины при разных входных комбинациях.

Например, комбинации 010 и 011 возбуждают одну и ту же шину t2.

б) Одной комбинацией одновременно возбуждать несколько вертикальных шин, например, комбинация 010 возбуждает шину t1 и t2.

в) Некоторые комбинации не возбуждают ни одной шины: например, комбинации 000, 111.

Таким образом, применение ПЛМ целесообразно в тех случаях, когда:

а) используются не все кодовые комбинации входного кода,

б) некоторым входным комбинациям соответствует одна и та же комбинация выходного кода.

Функциональные возможности ПЛМ определяются значениями трех ее параметров:

числом входов – m,

числом выходов – n,

числом выходов матрицы М1–t , что

то же самое числом термов – l.

Пример серийно выпускаемых ПЛМ: К556РТ1, РТ2 ( у них m=16, n=8, t=48).

§ 9.3. ПМЛ – программируемая матрица логики (PAL).

Иногда при реализации логических функций логическая мощность ПЛМ (это возможность реализации определенного числа функций в одной ПЛМ) используется не полностью. Это проявляется, в частности, при воспроизведении типичных функций, не имеющих пересечений по одиночным термам, то есть разные функции имеют мало одинаковых терм. В этих случаях возможность использования выходов любых конъюнкторов разными дизъюнкторами в ПЛМ становится ненужной, то есть матрицу М2 (элементов ИЛИ) можно не программировать, что приводит к упрощению ее изготовления.

Это обстоятельство и привело к появлению ПМЛ, в которой выходы элементов И (матрицы М1) жестко связаны со входами определенных ИЛИ матрицы М2. Базовая структура ПМЛ приведена на рис.9.07.

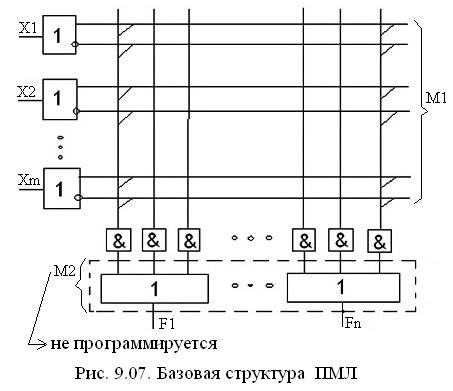
Подготовка задач к их решению на ПМЛ имеет много общего с подготовкой для ПЛМ, но есть и различия:

Для ПМЛ следует уменьшать число элементов И для каждого ИЛИ, для ПЛМ надо искать представление функций с наибольшим числом общих термов, а для ПМЛ этого не требуется.