Глава 5. Сумматоры.

§ 5.1 Полусумматор. Инкрементор.

Схему сложения двух чисел: переноса Сr и числа А называют полусумматором.

Функции, реализуемые полусумматором, приведены на рис. 5.1 а), а его схема на рис. 5.1 б). УГО полусумматора на рис. 5.1 в).

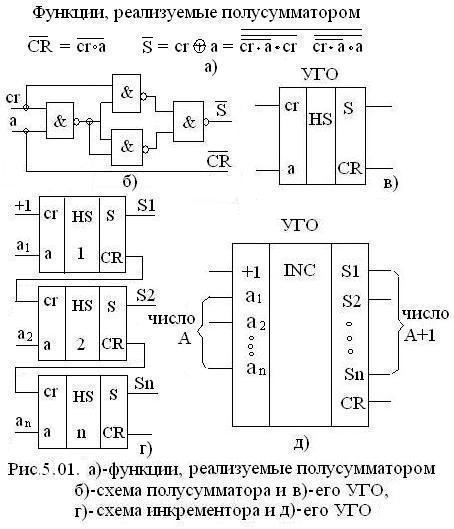
Полусумматоры, соединенные последовательно по цепи переносов, образуют инкрементор, который иногда называют накапливающим сумматором. Схема инкрементора и его УГО показаны на рис. 5.1 г) и д) соответственно.

При подаче на вход +1 «0»икрементор записывает число А без изменения.

Если на этот вход подать «1», то он прибавляет ее к числу А (выход А+1).

В инкременторе число А и А+1 существует только одновременно на входе и выходе, то есть схема инкрементора является схемой без памяти. Инкрементор можно построить и с параллельным переносом или групповым.

По аналогии с инкрементором строится и декрементор – узел, уменьшающий число А на «1», если на вход займа «-1» подать единичный сигнал (строится по аналогии со сдвигающим RG влево).

§5.2 Сумматор.

Н а основании таблицы суммирования двух разрядов чисел А и В (рис.5.2) можно составить логические выражения при суммировании для суммы S и переноса CR (выражения ).

Основная задача – минимизировать эти функции. После минимизации получим функции суммирования для суммы S и переноса CR. На основании функций можно построить одноразрядный сумматор – рис.5.3 а).

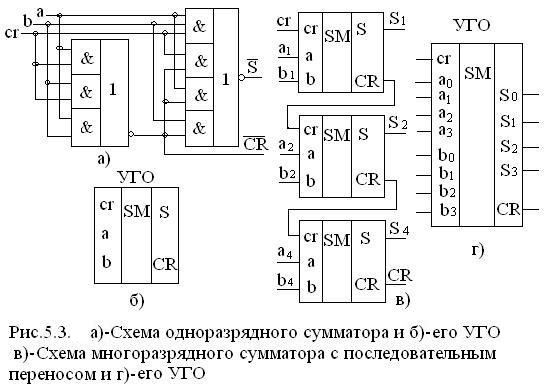
Следует отметить, что схема одноразрядного сумматора, построенная на основании функций в базисе И-ИЛИ-НЕ имеет 17 выводов, что в 2 раза меньше, чем в схеме, построенной на основании функций (цена минимизации).

Задержка сумматора: для S – 1τ , для CR – 2τ. Последовательным соединением одноразрядных сумматоров по тракту переноса CR получен многоразрядный сумматор с последовательным переносом (рис.5.3 в), его УГО на рис.5.3 г.

Особенности схемы.

На входе одноразрядного сумматора сигнал cr, а на выходе – 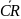, следовательно, между разрядами надо ставить инверторы, что увеличивает задержку многоразрядного сумматора. Поэтому на практике для решения этой проблемы используется свойство самодвойственности логических функций: значение функции интерпретируется при инвертировании ее входных аргументов. Это видно из сравнения строк таблицы суммирования (рис.5.2): 3 и 4, 2 и 5, 1 и 6, 0 и 7. Исходя из этого факта при построении многоразрядного последовательного сумматора тракты переноса CR соединяются напрямую, а на те разряды, на которые поступает инверсный перенос , входные аргументы инвертируют и получают на выходе CR без инверсии. Если на входы разрядов сумматора данные подаются с выходов регистра (это чаще всего и делается), то данные для соответствующих разрядов снимаются с инверсных выходов этого регистра.

По определению сумматором называют комбинационное логическое устройство для выполнения арифметического сложения двух чисел, представленных в двоичном коде. Сумматор является основным узлом арифметико-логического устройства ЭВМ – ALU.

Сумматор имеет:

n – входов разрядов числа А.

n – входов разрядов числа В.

cr – вход переноса из младшего разряда сумматора.

CR – выход переноса в старший разряд сумматора.

n – выходов разрядов суммы S.

Задержки распространения сигналов:

t_cr,S – от входа переноса до установления суммы S.

t_А,S– от входов слагаемых до выходов S при cr – const.

t_cr,CR– от входа cr до выхода CR при постоянных слагаемых.

t_A,CR– от входа слагаемых до выхода CR.

Задержка многоразрядного сумматора с последовательным переносом:

t_{cr вх,СR вых}= t_cr1,CR1+ t_cr2,CR2+… +t_{cr n,CR n}=n t_cr,CR,

где n – число разрядов в сумматоре,

t_cr,CR – задержка в одном разряде.

Примеры серийно выпускаемых сумматоров:

К155ИМ1 – двухразрядный, данные вводятся с регистра – прямой и инверсный выход,

К155ИМ-2,3 – четырехразрядные, с переносом через разряд, используется инвертор.

Иногда в сумматорах для решения проблемы переносов в разрядах используются сумматоры с двухколейным переносом (рис. 5.4 а и б).

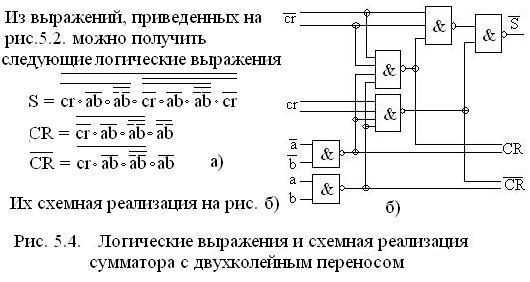
Логические функции суммирования (а) получены из соотношений (рис. 5.2). Схема реализации рис. 5.4 б.

Особенности схемы: перенос вырабатывается парафазным кодом по двум трактам CR и , что позволяет при построении многоразрядного сумматора для переноса между разрядами CR или для получения суммы всегда одной фазности.