- •Нелинейные резистивные электрические цепи постоянного тока. Нелинейные резистивные элементы (лампа накаливания, бареттер, стабилитрон, диод).
- •Методы расчета нелинейных резистивных цепей постоянного тока.
- •8.2.1. Аналитические методы расчета нелинейных цепей
- •8.2.2. Графические методы расчета нелинейных цепей
- •1) Метод эквивалентных преобразований (сложения характеристик)
- •2) Метод двух узлов
- •3) Метод эквивалентного генератора
- •8.2.3. Численный расчет нелинейных резистивных цепей
- •Расчет нелинейной резистивной цепи постоянного тока с двумя узлами. Применение метода активного двухполюсника при расчете нелинейных резистивных цепей постоянного тока.
- •Нелинейные резистивные электрические цепи переменного тока. Электрический вентиль, стабилитрон: вольтамперные характеристики, применение.
- •Однополупериодное выпрямление и его характеристики.
- •Двухполупериодное выпрямление и его характеристики.
- •Расчет нелинейных резистивных цепей переменного тока методом кусочно-линейной аппроксимации.
- •Графический метод расчета нелинейных резистивных цепей переменного тока.
- •Основные законы и особенности магнитных цепей постоянного магнитного потока. Допущения при расчете магнитных цепей.
- •8.3.2. Допущения, принимаемые при расчете магнитных цепей.
- •Расчет прямой и обратной задач в магнитных цепях постоянного тока. Законы Кирхгофа для магнитных цепей.
- •Катушка со стальным сердечником. Форма кривых тока, напряжения и потока (питание от источника тока).
- •Катушка со стальным сердечником. Форма кривых тока, напряжения и потока (питание от источника напряжения). См 11 !!
- •Расчет нелинейных магнитных цепей методом кусочно-линейной аппроксимации.
- •Расчет нелинейных индуктивных цепей по мгновенным значениям (аналитический метод расчета).
- •Метод эквивалентных синусоид. Расчет катушки со стальным сердечником методом эквивалентных синусоид.
- •Феррорезонанс напряжений. Идеальная и реальная вольтамперная характеристики.
- •Феррорезонанс токов. Идеальная и реальная вольтамперная характеристики.
- •Переходные процессы в нелинейных цепях. Особенности, методы расчета.
- •9.1. Особенности расчета переходных процессов в нелинейных цепях
- •9.2. Выход на установившийся режим
- •Аналитические методы расчета переходных процессов в нелинейных цепях (метод условной линеаризации, кусочно-линейной аппроксимации).
- •Аналитические методы расчета переходных процессов в нелинейных цепях (кусочно-линейной аппроксимации, аппроксимации полиномом).
- •3) Метод аналитической аппроксимации нелинейной характеристики
Катушка со стальным сердечником. Форма кривых тока, напряжения и потока (питание от источника напряжения). См 11 !!
Намагничивание от источника синусоидального тока.
Если требуется найти кривую напряжения на катушке с ферромагнитным сердечником и известным синусоидальным током i(t)=Imsin(ωt), то пренебрегая влиянием вихревых токов и гистерезисом при графическом решении сначала строят кривую потокосцепления (рис. 8.46). Графически дифференцируя кривую потокосцепления, находят искомую кривую напряжения. При этом вследствие затупленной формы кривой потокосцепления кривая напряжения имеет весьма заостренную форму и искажена значительно больше, чем кривая тока в предыдущем случае.
При аналитическом расчете реальную характеристику Ψ(i) или Φ(i) аналитически аппроксимируют полиномом Φ(i)=b1i-b3i3 ( коэффициенты b1 и b3 в простейшем случае находят из рассмотрения рабочего участка, определяемого амплитудой входного напряжения). Так как i(t)=Imsin(ωt), то Φ(t)=b1Imsin(ωt)-b3(Imsin(ωt))3. С учетом того, что , мгновенное значение потокосцепления
|
При аналитической аппроксимации полиномом кривая потокосцепления содержит первую и третью гармоники Ψ(t)=Ψ1msin(ωt)+Ψ3msin(3ωt). Напряжение на катушке u(t)=dΨ/dt, т.е. u(t)=ωΨmcos(ωt)+3ωΨ3mcos(3ωt)=U1mcos(ωt)+U3mcos(3ωt).
|
Рис. 8.46 |
Расчет нелинейных магнитных цепей методом кусочно-линейной аппроксимации.
При кусочно-линейной аппроксимации характеристики Ψ(i) или i(Ψ) заменяют отрезками прямых. На каждом участке задача решается как линейная, результирующая кривая тока или напряжения катушки состоит из частей отдельных синусоидальных кривых, сопряженных в углах отсечки ( в угловых единицах моменты перехода в одного участка линейности не другой). Наиболее эффективен метод в случае, если отрезки прямых могут быть взяты параллельными или совпадающими с осями координат. Расчеты цепи, проведенные при прямоугольной аппроксимации, дают возможность получить численные соотношения между электрическими величинами при максимально возможной степени нелинейности.
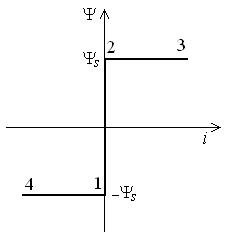
На рис. 8.47 изображена идеальная кривая намагничивания, индуктивный элемент с такой характеристикой представляет собой магнитный ключ. На рис 8.48 показана схема цепи, содержащая нелинейный индуктивный элемент и линейный резистор.
|
|
Рис. 8.47 |
Рис. 8.48 |
Пусть
на входе цепи – источник напряжения
u(t)=Umsin(ωt).
На участке 1-2 -Ψs
≤ Ψ≤
Ψs
ток в цепи i(t)=0
и все напряжение приложено к нелинейной
катушке
![]() .
Потокосцепление меняется по косинусному
закону
.
Потокосцепление меняется по косинусному
закону
![]() .
Константа С
выбирается из условия, что при t=0
Ψ(0)=-Ψs,
т.е. -Ψm+C=-Ψs
и C=-Ψs+Ψm.
При ωt=θα потокосцепление
станет равным Ψs,
на участке 2-3 θα
≤ ωt ≤ π
потокосцепление меняться не будет
Ψ=Ψs
и напряжение на нелинейной катушке
uL(t)=0.
Переход на горизонтальный участок
означает скачкообразное появление тока
в цепи
.
Константа С
выбирается из условия, что при t=0
Ψ(0)=-Ψs,
т.е. -Ψm+C=-Ψs
и C=-Ψs+Ψm.
При ωt=θα потокосцепление
станет равным Ψs,
на участке 2-3 θα
≤ ωt ≤ π
потокосцепление меняться не будет
Ψ=Ψs
и напряжение на нелинейной катушке
uL(t)=0.
Переход на горизонтальный участок
означает скачкообразное появление тока
в цепи
![]() .
В силу периодичности процесса при ωt=π
ток должен быть равен нулю. Угол
насыщения θα
может быть определен из условия
Ψ(θα)=Ψs,
т.е.
.
В силу периодичности процесса при ωt=π
ток должен быть равен нулю. Угол
насыщения θα
может быть определен из условия
Ψ(θα)=Ψs,
т.е.
![]() .
В силу периодичности процесса участки
2-1 и 1-4 рассчитываются аналогично. На
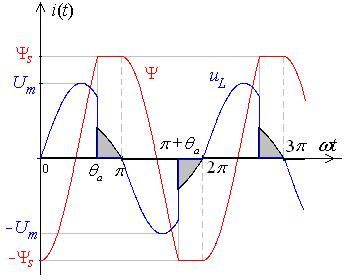
рис.8.49 изображены кривые потокосцепления,
напряжения на катушке и тока в цепи.
.
В силу периодичности процесса участки
2-1 и 1-4 рассчитываются аналогично. На
рис.8.49 изображены кривые потокосцепления,
напряжения на катушке и тока в цепи.
|
Рис. 8.49 |