45. Характеристическим уравнением матрицы

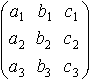
называется уравнение

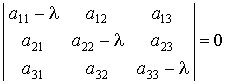
Корни этого уравнения l₁, l₂, l₃ называются характеристическими числами матрицы; они всегда вещественны, если исходная матрица была симметрической.    Система уравнений

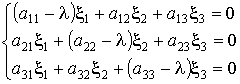
в которой l имеет одно из значений l₁, l₂, l₃ и определитель которой в силу этого равен нулю, определяет тройку чисел (x₁, x₂, x₃), соответствующую данному характеристическому числу.    Эта совокупность трех чисел (x₁, x₂, x₃) определяет вектор r=₁i+₂j+₃k, называемый собственным вектором матрицы.