5.4.3. Итеративные коды.

На основе (n, n-1) – кодов с d_min=2 или кодов Хэмминга с d_min=3 и d_min=4 можно построить коды с более высокими корректирующими свойствами. Для этой цели, наряду с защитой каждой передаваемой комбинации описанным выше способом, осуществляют помехоустойчивое кодирование одноименных разрядов групп передаваемых комбинаций. Процесс кодирования можно пояснить при помощи рис. 5.6.

Комбинации простого кода, подлежащие передаче по системе связи, записываются в виде таблицы – каждая комбинация составляет отдельную строку этой таблицы (информационные символы). Затем осуществляется кодирование по строкам и столбцам. В общем случае для кодирования строк и кодирования столбцов можно использовать различные коды. Избыточные элементы дописываются к каждой строке (проверка по строкам) и к каждому столбцу (проверка по столбцам). Проверка проверок осуществляется кодированием столбцов, составленных из избыточных элементов строк или кодированием строк, составленных из проверок столбцов. Процесс кодирования поясняется на рис. 5.6.

В результате итеративного кодирования получаются групповые коды, которые обладают следующим важным свойством.

Теорема 5.3. Минимальное кодовое расстояние итеративного кода равно произведению минимальных кодовых расстояний, кодов, его составляющих.

Действительно, если в случае двух проверок минимальный вес одного кода равен , а другого , то вектор итеративного кода имеет, по крайней мере, единиц в каждой строке и элементов в каждом столбце и, следовательно, не менее единиц.

Аналогичные рассуждения можно продолжить и на случай большего числа проверок.

Порождающая матрица итеративного кода может быть построена следующим образом.

Пусть G_A – порождающая матрица кода, используемого для проверки по строкам, а G_В – порождающая матрица кода, используемого для проверки по столбцам, тогда порождающая матрица итеративного кода (G_AВ) имеет вид:

.

Запись означает, что на местах “1” в матрице G_A записывается матрица G_В, а вместо “0” записывается матрица из одних нулей, размеры которой равны размерам G_В. Так, например, если для проверки по строкам и столбцам используется (6, 5) – код с проверкой на четность, то

,

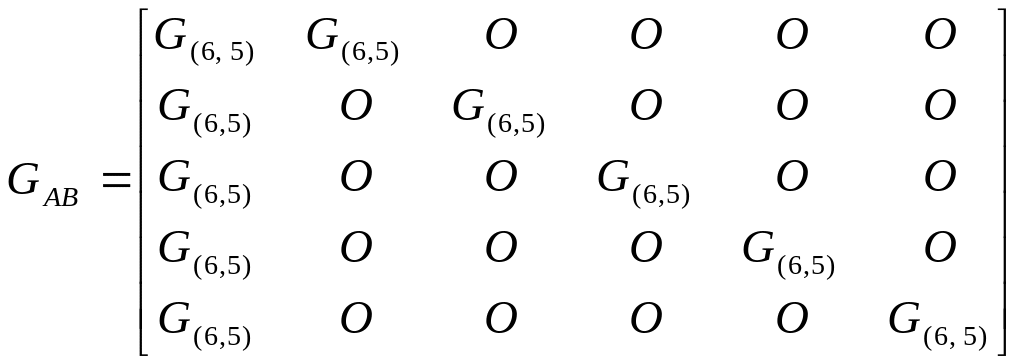где

.

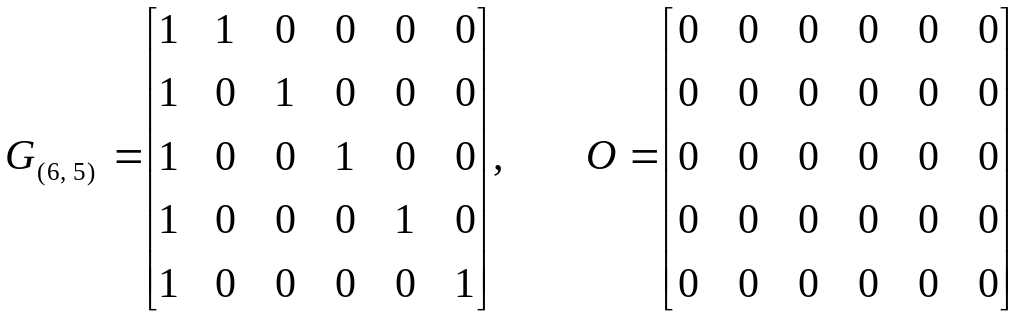4. Задачи

1. Показать, что корректирующие свойства (6, 5) – кода, в котором избыточный элемент вводится как проверка на нечетность, в точности совпадают с корректирующими свойствами (6, 5) – кода с проверкой на четность.

2. Показать, что коды Хэмминга с d_min=3 соответствуют границе Хэмминга.

3. Показать, что (7, 3) – код, являющийся нулевым пространством кода Хэмминга (7, 4), является эквидистантным, т.е. все кодовые расстояния в этом коде равны.

4. Построить порождающую матрицу для итеративного кода, в котором по строкам и столбцам используется (8, 7) – код с проверкой на четность.

Тема 6. Двоичные циклические (n,k) - коды

6.1. Основные алгебраические системы, используемые в теории кодирования.

(Продолжение раздела 5.2.1.)

Выше, в разделе 5.2.1 были введены понятия группы и векторного пространства, которые лежат в основе определения и описания групповых кодов. Для изучения важного подкласса групповых кодов – циклических кодов – необходимо знакомство и с другими алгебраическими системами, такими как кольцо и поле.

в) Кольцо

Кольцом R называют множество элементов, на котором определены две операции – сложение a + b и умножение ab. Для того, чтобы R было кольцом оно должно удовлетворять следующим требованиям:

R.1 Множество R является абелевой группой по операции сложения (аддитивная абелева группа).

R.2 (замкнутость). Для любых двух элементов a и b из множества R определено произведение ab, которое является элементом R.

R.3 (ассоциативный закон). Для любых трех элементов a, b, и c из R a(bc)=(ab)c.

R.4 (дистрибутивный закон). Для любых трех элементов a, b, и c из множества R справедливы равенства a(b+c)=ab+ac и (b+c)a=ba+ca.

Кольцо называют коммутативным, если операция умножения коммутативна, т.е. для любых двух элементов R выполняется равенство ab=ba.

В теории групп очень важную роль играет понятие подгруппы. В теории колец соответствующую роль играет понятие идеала. Идеалом I называют подмножество элементов кольца R, обладающее следующими двумя свойствами:

1). I является подгруппой аддитивной группы кольца R;

2). Для любого элемента a из I и любого элемента r из R произведения ar и ra принадлежат I.

Поскольку идеал является подгруппой, могут быть образованы смежные классы (см. основные свойства группы). В этом случае смежные классы называют классами вычетов. Идеал образует первую строку разложения с нулевым элементом (единичным элементом по операции сложения) слева. Далее любой элемент кольца, не принадлежащий идеалу, может быть выбран в качестве образующего первого класса вычетов, а остальные элементы класса получают прибавлением образующего к каждому элементу идеала:

0=a1,	a2,	a3,	a4,	a5,…
r1=r1+a1,	r1+a2,	r1+a3,	r1+a4,	r1+a5,…
r2=r2+a1,	r2+a2	r2+a3,	r2+a4,	r2+a5,…
…….	…….	…….	…….	…….
…….	…….	…….	……..	…….
…….	…….	…….	…….	…….

Первыми элементами в каждой строке являются, как и при построении смежных классов, элементы, не использованные в предыдущих строках.

Все свойства смежных классов верны также для классов вычетов:{r}+{s}={r+s} и умножение классов вычетов {r}{s}={rs}

В высшей алгебре доказывается, что классы вычетов по идеалу в некотором кольце образуют кольцо. Это кольцо называют кольцом классов вычетов.

В теории кодирования важную роль играют кольца целых чисел и кольца многочленов.

Основные свойства кольца:

1. Совокупность целых чисел образует идеал тогда и только тогда, когда она состоит из всех чисел, кратных некоторому целому числу.

Пусть m – наименьшее целое положительное число в идеале и s – любое другое кольцо в идеале. На основе алгоритма деления Евклида запишем выражение для наибольшего общего делителя чисел m и s:

d=am+bs,

где a и b - целые числа.

Из приведенного равенства вытекает, что d также принадлежит идеалу. Действительно, так как m – наименьшее число в идеале, то m≤d, а так как d делит m, то d≤m. Значит m=d и s кратно m.

Идеал, который состоит из всех чисел, кратных m и самого m, обозначают (m).

2. Каждый класс вычетов по модулю m содержит либо 0, либо целое положительное число, не превосходящее m. Нуль является элементом идеала, а все целые положительные числа, не превосходящие m, принадлежат различным классам вычетов.

Доказательство этого свойства основывается на рассуждениях, приведенных в примере 5.2.2.

Построенные в этом примере смежные классы являются также и классами вычетов по идеалу (2) и образуют кольцо целых чисел по модулю 2.

Сформулированные выше свойства колец целых чисел полностью справедливы и для многочленов. Сходство в строении и свойствах кольца целых чисел и кольца многочленов обусловлены тем, что оба они являются частными случаями алгебраического образования, известного как евклидово кольцо. Рассмотрим основные свойства колец многочленов, необходимые для понимания структуры циклических кодов.

3. Совокупность многочленов образует идеал тогда и только тогда, когда она содержит все многочлены кратные некоторому многочлену.

Идеал, образованный всеми многочленами, кратными f(x) обозначают (f(x)). Кольцо классов вычетов, образованных по этому идеалу, называют кольцом многочленов по модулю f(x).

4. Каждый класс вычетов по модулю многочлена f(x) степени n содержит либо 0, либо многочлен степени меньшей, чем n. Нуль является элементом идеала, а все многочлены степеней, меньших, чем n, принадлежат различным классам вычетов.

Пример 6.1. Особую роль в теории циклических кодов играет кольцо многочленов по модулю двучлена xⁿ+1

Рассмотрим классы вычетов многочленов по модулю двучлена третьей степени – x³+1. В соответствии со свойством 4 каждый класс вычетов содержит либо 0, либо многочлен степени меньшей, чем 3. Как и ранее рассматриваем многочлены с коэффициентами в виде двоичных элементов. Приведенная ниже таблица отражает содержание классов вычетов многочленов по модулю многочлена x³+1

{0}=000	1+x3	x(1+x3)	. . .
{1}=100	X3	1+x+x4	. . .
{x}=010	1+x+x3	x4	. . .
{1+x}=110	X+x3	1+x4	. . .
{x2}=001	1+x2+x3	x+x2+x4	. . .
{1+x2}=101	X2+x3	1+x+x2+x4	. . .
{x+x2}=011	1+x+x2+x3	x2+x4	. . .
{1+x+x2}=111	X+x2+x3	1+x2+x4	. . .

В левой колонке этой таблице приведены многочлены минимальной степени в своем классе вычетов. Именно они обозначают класс вычетов и поэтому взяты в фигурные скобки. Рядом с ними показано двоичном представление многочленов данного класса вычетов.

Двоичное представление класса вычетов показывает, что классы вычетов представляют собою векторное пространство размерности 3, состоящее из 8 двоичных последовательностей длины 3.

Из приведенного примера можно сделать следующий очень важный вывод: кольцо многочленов по модулю двучлена xⁿ+1 отображает бесконечное множество многочленов на конечное n – мерное векторное пространство. При этом векторы этого пространства можно складывать и умножать по правилам сложения и умножения классов вычетов многочленов по модулю xⁿ+1.

Кольцо многочленов по модулю двучлена xⁿ+1, как и любое кольцо, имеет свой идеал. Как и в случае целых чисел, идеал I кольца многочленов по модулю xⁿ+1 содержит классы вычетов, кратные некоторому классу вычетов {g(x)}, т.е. некоторый класс вычетов {s(x)}, принадлежит идеалу I тогда и только тогда, когда s(x) делится на g(x). Покажем, что g(x) при этом должен быть делителем xⁿ+1.

Представим процесс деления xⁿ+1 на g(x) в следующем виде:

xⁿ+1=g(x)q(x)+r(x),

где q(x)- частное от деления, а r(x)-остаток от деления. При этом, очевидно, что степень r(x)- меньше степени g(x).Поэтому должно быть справедливо равенство:

{0}={xⁿ+1}={g(x)}{q(x)}+{r(x)},

из которого вытекает, что класс вычетов {r(x)} также принадлежащий идеалу I. Поскольку степень r(x) меньше степени g(x), то r(x) должно быть нулевым и, следовательно, xⁿ+1 кратен g(x).

Пример 6.2. Определим, какие идеалы существуют в кольце многочленов Примера 6.1. Рассматриваемое кольцо образуют классы вычетов многочленов по модулю x³+1. X³+1 имеет в качестве сомножителей два многочлена с двоичными коэффициентами:

x³+1=(x+1)(x²+x+1).

Следовательно, имеется два подмножества последовательностей длины 3, образующие идеалы рассматриваемого кольца. Один идеал включает все классы вычетов кратные {1+x}: {0}, {1+x}, {1+x²}, {x+x²}, отображаемые двоичными последовательностями (000), (110), (101) и (011) соответственно. Второй идеал состоит из классов вычетов {0} и {1+x+x²}, отображаемых двоичными последовательностями (000) и (111).

Представляет интерес сравнить полученные идеалы с результатами решения задач 2 и 5 из раздела 5.2.5.

5. Пусть xⁿ+1=g(x)·h(x), где h(x)-многочлен степени k. Тогда идеал, порожденный классом вычетов {g(x)} в кольце многочленов по модулю xⁿ+1, имеет размерность k.

Действительно, многочлен g(x),порождающий идеал, имеет степень n-k, а значит среди классов вычетов кольца многочленов по модулю xⁿ+1 существуют классы вычетов {g(x)}, {xg(x)},…{x^k-1g(x)},отображаемые k линейно независимыми векторами. При этом любой класс вычетов может быть представлен вектором, полученным линейной комбинацией. Например, S(x) - многочлен минимальной степени в своей классе вычетов и S(x)=g(x)·q(x)=g(x)(q₀+q₁x+…+q_k-1x^k-1) и {S(x)}=q₀{g(x)}+q₁{xg(x)}+…+q_k-1{x^k-1g(x)}, т.е k векторов {g(x)}, {xg(x)},…, {x^k-1g(x)} порождают идеал. Значит размерность идеала, равна k.

В примере 6.2. один из идеалов порождается векторами {g(x)}={1+x} и {xg(x)}={x+x²}, а другой – {1+x+x²}.

Многочлен g(x) минимальной степени, такой, что его класс вычетов {g(x)} принадлежит идеалу, называет порождающим многочленом идеала.

г) Понятие о конечных полях

Полем называют множество элементов, на котором определены две операции. Одна из них называется сложением и обозначается a+b, а другая – умножением и обозначается ab, даже если эти операции не являются обычными операциями сложения и умножения чисел. Для того чтобы множество элементов, на котором заданы операции сложения и умножения, было полем, необходимо, чтобы по каждой из этих операций выполнялись все групповые аксиомы, а также выполнялся дистрибутивный закон, т.е. для трех любых элементов поля а, b, с были справедливы равенства а(b+с)=аb+ас и (b+с)а=bа+са.

Кроме того, по каждой операции группа должна быть коммутативной, т.е. должно выполняться, а+b=b+a и аb=bа. Следует заметить, что групповые свойства по операции умножения справедливы для всех ненулевых элементов поля.

Поля с конечным числом элементов q называют полями Галуа по имени их первого исследователя Эвариста Галуа и обозначают GF(q).

Число элементов поля q называют порядком поля. Конечные поля используются для построения большинства известных кодов и их декодирования.

В зависимости от значения q различают простые или расширенные поля. Поле называют простым, если q – простое число. Для обозначения простых чисел будем использовать символ p.

Простое поле образуют числа по модулю p: 0, 1, 2,…, p–1. Операции сложения и умножения в простых полях выполняются по модулю p.

Наименьшее число элементов, образующих поле, равно 2. Такое поле должно содержать 2 единичных элемента: 0 относительно операции сложения и 1 относительно операции умножения. Это поле (GF 2), или двоичное.

Правила сложения и умножений для элементов GF(2) задаются таблицами:

Таблица сложения : Таблица умножения:

	+	0	1		×	0	1
	0	0	1		0	0	0
	1	1	0		1	0	1

GF(3) – троичное поле с элементами 0, 1, 2. Для него таблица сложения и умножения имеют вид.

+	0	1	2		×	0	1	2
0	0	1	2		0	0	0	0
1	1	2	0		1	0	1	2
2	2	0	1		2	0	2	1

Формирование таблиц производится приведением результата сложения или умножения чисел, записанных во главе строк или столбцов, по модулю p, т.е. в качестве результата операции принимается остаток от деления полученного числа на p.

Анализируя состав таблиц, легко убедиться, что 0 и 1 как единичные элементы по операции сложения и умножения не изменяют значения других элементов поля по соответствующей операции. Кроме того, видно, что для каждого элемента по операции сложения и для ненулевых элементов по операции умножения имеются обратные.

Ниже приведены правила сложения и умножения для элементов GF(4) при попытке построить это поле из чисел 0, 1, 2, 3 по предыдущей конструкции.

Таблица сложения: Таблица умножения:

	+	0	1	2	3		×	0	1	2	3
	0	0	1	2	3		0	0	0	0	0
	1	1	2	3	0		1	0	1	2	3
	2	2	3	0	1		2	0	2	0	2
	3	3	0	1	2		3	0	3	2	1

Из анализа таблиц видно, что для элемента 2 по операции умножения отсутствует обратный, т.е. набор чисел 0, 1, 2, 3 не является полем при введении операции по модулю 4. Такой результат объясним тем, что 4 не является простым числом. Для поля GF(5) с элементами 0, 1, 2, З, 4 правила сложения и умножения имеют вид.

Таблица сложения: Таблица умножения:

	+	0	1	2	3	4		×	0	1	2	3	4
	0	0	1	2	3	4		0	0	0	0	0	0
	1	1	2	3	4	0		1	0	1	2	3	4
	2	2	3	4	0	1		2	0	2	4	1	3
	3	3	4	0	1	2		3	0	3	1	4	2
	4	4	0	1	2	3		4	0	4	3	2	1

Изучим возможность построения полей с элементами в виде последовательностей чисел.

Определим условия, при которых последовательности длины m с элементами из поля GF(p) образуют поле.

Рассмотрим последовательности длины 4 с элементами из GF(2). Такие последовательности можно складывать как векторы, и нулевым элементом по операции сложения является 0000. Для задания операции умножения сопоставим каждой последовательности многочлен от α:

Последовательность	Многочлен
0 0 0 0	0
1 0 0 0	1
0 1 0 0	α
1 1 0 0	1+α
0 0 1 0	α2
1 0 1 0	1+α2
0 0 0 1	α3
…	…
1 1 1 1	1+α+α2+α3

Умножение таких многочленов может дать степень, большую, чем 3, т.е. последовательность, не принадлежащую рассматриваемому множеству.

Например, (1101)∙(1001)(1+α+α³)∙(1+α³)=1+α+α⁴+α⁶. Для того чтобы свести ответ к многочлену степени не более 3, положим, что α удовлетворяет уравнению степени 4, например:

Π(α)=1+α+α⁴=0,

или

α⁴=1+α.

Тогда

α⁵=α+α²,α ⁶=α²+ α³;

1+α+α ⁴+α⁶=1+α+1+α+α²+α³=α²+α³.

Это эквивалентно делению на многочлен 1+α+α⁴ и нахождению остатка от деления:

Щ+	α6+α4+α+1			α4+α+1
	α6+α3+α2			α2+1
=+	α4+α3+α2+α+1
	α4+α+1
	α3+α2–остаток

Таким образом, имеет место аналогия при формировании поля из чисел и последовательностей чисел (многочленов). Эта аналогия распространяется и на то, что для обратимости введенной операции умножения (чтобы система элементов в виде последовательностей длины m или многочленов степени меньшей m, образовывала поле) многочлен Π() должен быть неприводим над полем своих коэффициентов.

Поле, образованное многочленами над полем GF(р) по модулю неприводимого многочлена степени m, называется расширением поля степени m над GF(p) или расширенным полем. Оно содержит p^m элементов и обозначается GF(p^m).

Поле, образованное шестнадцатью двоичными последовательностями длины 4, или многочленами степени 3 и менее с коэффициентами из GF(2) по модулю многочлена α⁴+α+1 , неприводимого над GF(2), является примером расширенного поля GF(2⁴), которое может быть обозначено также GF(16)

Важнейшим свойством конечных полей является следующее.

Множество всех ненулевых элементов конечного поля образует группу по операции умножения, т.е. мультипликативную группу порядка q–1.

Рассмотрим совокупность элементов мультипликативной группы, образованную некоторым элементом α и всеми его степенями α², α³ и т.д. Так как группа конечна, должно появиться повторение, т.е. αⁱ=α^j. Умножая это равенство на (αⁱ)^–1 = (α^–1)ⁱ, получим 1=α^j-i. Следовательно, некоторая степень α равна 1.

Наименьшее положительное число e, такое, что α^e=1, называется порядком элемента α. Совокупность элементов 1, α, α²,…, α^e–1 образует подгруппу, поскольку произведение любых двух элементов принадлежит этой совокупности, а элемент, обратный α^j, равен α^e–j и тоже входит в эту совокупность.

Группа, которая состоит из всех степеней одного из ее элементов, называется циклической группой.

Из рассмотренного свойства конечных полей вытекают два важных следствия.

Первое из них утверждает, что многочлен x^q–1–1 имеет своими корнями все q–1 ненулевых элементов поля GF(q), т.е.

В поле GF(q) элемент α, имеющий порядок e=q–1, называется примитивным. Отсюда следует, что любой ненулевой элемент GF(q) является степенью примитивного элемента. Второе следствие из рассмотренного свойства утверждает, что любое конечное поле GF(q) содержит примитивный элемент, т.е. мультипликативная группа GF(q). является циклической

В табл..6.1 представлены различными способами элементы GF(2⁴).

Таблица 6.1

Последовательность длины 4	Многочлен	Степень	Логарифм
1	2	3	4
0000	0	0	–∞
1000	1	α0	0
0100	α	α	1
0010	α2	α2	2
0001	α3	α3	3
1100	1+α	α4	4
0110	α+α2	α5	5
0011	α2+α3	α6	6
1101	1+α+α3	α7	7
1010	1+α2	α8	8
0101	α+α3	α9	9
1110	1+α+α2	α10	10
0111	 + 2+ 3	11	11
1111	1++2+3	12	12
1011	1+2+3	13	13
1001	1+3	14	14

Поле GF(2⁴), представленное в табл. 6.1, построено по модулю α⁴+α+1. Примитивный элемент поля  является корнем этого многочлена.

Многочлен, корнем которого является примитивный элемент поля, называется примитивным многончлеом. Если в качестве Π(α) выбрать примитивный неприводимый многочлен степени m над полем GF(2), то получим поле GF(2^m) из всех 2^m двоичных последовательностей длины m.

Выше было показано, что GF(4) нельзя представить в виде совокупности чисел 0, 1, 2, 3. Построим его как расширенное поле по модулю многочлена Π(α) =α²+α+1 .

В табл. 6.2 элементы этого поля представлены различными способами. Здесь принято, что примитивный элемент  является корнем Π(), т.е. ²++1=0.

Таблица 6.2

Последовательность длины 2	Многочлен	Степень	Логарифм
00	0	0	–∞
10	1	1	0
01			1
11	1+	2	2

Правила сложения и умножения в этом поле приведены ниже.

Таблица сложения Таблица умножения

1	1+	10	11	1	12	1	1×	10	11	1	2
	10	10	11	1	12		10	10	10	10	10
	11	11	10	2	1		11	10	11	1	2
	1	1	12	10	11	1	1	10	1	2	11
	12	12	1	11	10	1	12	10	12	11	1

Формирование первой строки, первого столбца и диагональных элементов таблицы сложения, а также двух первых строк и двух первых столбцов таблицы умножения не вызывает затруднения.

Поясним формирование других элементов:

1+=², 1+²=, +²=1;

∙²=³= (1+)=+²=1

на основе соотношения для примитивного элемента ²++1=0.