Доказательство единственности решения

Пусть и два решения (1) с общими начальными условиями . Этот интервал является пересечением интервалов, на которых существуют данные решения. Точка - принадлежит данному интервалу. Покажем, что если эти решения совпадают в некоторой точке 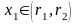, то они будут совпадать и на интервале , где r достаточно малое положительное число. Будем считать , тогда точка с координатами может играть роль начального значения для функции 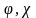. Поэтому, не нарушая общности, предположим, что совпадает с . Перейдем от дифференциальной постановки к интегральной:

. (19)

Рассмотрим прямоугольник с центром в точке . А затем более узкий прямоугольник 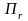. При этом будем считать, что r удовлетворяет (13),(16),(17). Этот значит, что функции удовлетворяют условию (14). Рассмотрим на отрезке , на этом отрезке они принадлежат 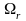, тогда 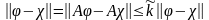, а это возможно только когда .

ОДУ 1-го порядка. Задача Коши. Общее решение

Цитировать

Обыкновенное дифференциальное уравнение 1-го порядка в общем случае имеет вид .

 

Если его удаётся разрешить относительно  , то будем иметь УДО вида

 

.

Иная форма записи последнего .

Простейшим обыкновенным дифференциальным уравнением 1-го порядка является  , решение которого выглядит как , где   — производная постоянная, то есть уравнение имеет бесчисленное множество решений.

 

О: Задача нахождения решения обыкновенного дифференциального уравнения, которое удовлетворяет начальному условию   (такая запись эквивалентна ) именуется задачей Коши.

 

Т. (о существовании и единственности задачи Коши): Если функция  и её частная производная   непрерывны в окрестности т.  , то в окрестностях т. имеется единственное решение   задачи Коши  ■

 

О: Общим решением обыкновенного дифференциального уравнения 1-го порядка называется функция  , которая удовлетворяет следующим условиям:

 

1. функция  является решением  ;

2. при любом начальном условии , имеется такое значение 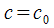 , при котором   удовлетворяет имеющемуся начальному условию. Точка 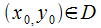  — области, где выполняются условия существования и единственности решения.

Пример:  — общее решение обыкновенного дифференциального уравнения. Пользуясь начальным условием  , определяем  , то есть — решение задачи Коши в области

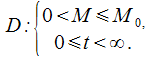
Примечание: Иногда общее решение обыкновенного дифференциального уравнения существует в неявном виде , тогда оно именуется общим интегралом.

 

О: Частным решением обыкновенного дифференциального уравнения 1-го порядка именуется функция   при данном значении  .

 

Геометрически такое решение представляет семейство кривых на плоскости  , которое находится в зависимости от  . Эти кривые именуются интегральными кривыми данного обыкновенного дифференциального уравнения 1-го порядка. При задании обыкновенного дифференциального уравнения в виде (20.3) определён угловой коэффициент касательных к интегральным кривым в каждой из точек  .

 

Примеры: 1) На рис. 20.1 показаны интегральные кривые дифференциального уравнения  , которое обладает общим решением  .

1. На рисунке 20.2 показаны интегральные кривые дифференциального уравнения (20.1), которое имеет решение .