Билет 2 Дифференциальные уравнения с разделяющимися переменными

Дифференциальное уравнение вида

или

называется дифференциальным уравнением с разделяющимися переменными.

Заметим, что в данных дифференциальных уравнениях каждая из функций зависит только от одной переменной, т.е. происходит разделение переменных.

Для решения такого дифференциального уравнения необходимо домножить или разделить обе части дифференциального уравнения на такое выражение, чтобы в одну часть уравнения входили только функции от   и   , в другую часть уравнения - только функции от   ,   . Затем в полученном дифференциальном уравнении надо проинтегрировать обе части:

Следует заметить, что при делении обеих частей дифференциального уравнения на выражение, содержащее неизвестные   и   , могут быть потеряны решения, обращающие это выражение в ноль.

Обратим внимание, что дифференциальные уравнения с разделяющимися переменными легко сводятся к интегрированию. В общем случае получаем получаем дванеопределенных интеграла.

Пример 1 - решить дифференциальное уравнение

Заметим, что в дифференциальном уравнении можно разделить переменные, т.е. получаем,дифференциальное уравнение с разделяющимися переменными:

Пример 2 - решить дифференциальное уравнение

Заметим, что в дифференциальном уравнении можно разделить переменные, т.е. получаем,дифференциальное уравнение с разделяющимися переменными:

Пример 3 - решить дифференциальное уравнение

Заметим, что в дифференциальном уравнении можно разделить переменные, т.е. получаем,дифференциальное уравнение с разделяющимися переменными:

Пример:

Найти решение дифференциального уравнения, удовлетворяющее заданным начальным условиям.   Решение Это уравнение с разделяющимися переменными. 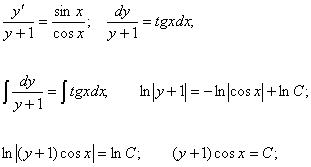Общее решение имеет вид: Найдем частное решение при заданном начальном условии у(0) = 0. Окончательно получаем:

Билет3

Однородные уравнения первого порядка.

Вопрос №18.

Однородные уравнения первого порядка.

Определение 1. Функция f{x,y) называется однородной функцией п-го измерения относительно переменных х и у, если при любой лямбде справедливо тождество: 

Определение 2. Уравнение первого порядка 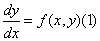 называется однородным относительно х и у, если функция f(x, у) есть однородная функция нулевого измерения относительно х и y.

Решение однородного уравнения.

По условию f(лямбда x, лямбда y) = = f(x, у). Положив в этом тождестве лямбда = 1/х, получим:  т.е. однородная функция нулевого измерения зависит только от соотношения аргументов. Уравнение (1) в этом случае примет вид 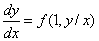 Сделаем подстановку: u=y/x, то есть y=ux. Тогда будем иметь: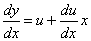 

Подставляя это выражение производной в уравнение (1'), получим:  .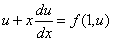

Это уравнение с разделяющимися переменными: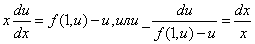 

Интегрируя, найдем: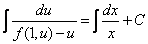

Подставляя после интегрирования вместо и отношение у/х, получим интеграл уравнения (1').

Билет 4

§ 6. Линейное уравнение первого порядка

1 Случай.

Линейным дифференциальным уравнением первого порядка называется уравнение вида

Здесь a(x) и b(x) — известные, непрерывные на [a;b] функции.

Доказано, что если функции a(x) и b(x) непрерывны на [a;b] , то для любой начальной точки (x₀, y₀) , x₀∈ [a; b] , задача Коши

имеет единственное решение y = y(x) на [a;b].

 

Рассматривают однородные и неоднородные линейные уравнения первого порядка:

 

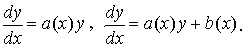
Общее решение линейного уравнения 1-го порядка можно найти с помощью замены y(x) = u(x) · v(x) .

Линейные дифференциальные уравнения первого порядка.

Линейным дифференциальным уравнением первого порядка называется уравнение вида

                                            ,                                                (1)

линейное относительно неизвестной функции   и ее производной. Если в уравнении (1) правая часть  , то уравнение

                                                                                                  (2)

называется линейным однородным уравнением, которое является уравнением с разделяющимися переменными.

Решим уравнение (2):

                                                ,

                          ,  ,

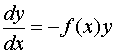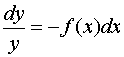                            , где   принимает любые

положительные и отрицательные значения, соответствующего данному неоднородному (то есть имеющее =такую же левую часть, что и уравнение (1)), то общее решение неоднородного уравнения может быть полученометодом вариации произвольной постоянной.

Полагая в решении однородного уравнения константу некоторой неизвестной функцией переменной  , запишем

                                                                                                (3)

Подставим выражение (3) в неоднородное уравнение (1):

        ,

                                                                                        (4)

Получено уравнение с разделяющимися переменными относительно неизвестной функции  , решив которое можно дописать общее решение неоднородного уравнения (1) в виде (3).

Из уравнения (4) имеем

                                     .

Возвращаясь к выражению (3), найдем

                      ,                          (5)

где первое слагаемое является частным решением неоднородного уравнения (1), а второе слагаемое – общим решением однородного уравнения (2).

Таким образом, общее решение неоднородного линейного уравнения может быть представлено в виде суммы

                                                   ,                                                       (6)

где   - общее решение соответствующего однородного уравнения, а   - некоторое частное решение неоднородного уравнения.

Метод вариации произвольной постоянной не единственный при решении линейных уравнений.

Удобным способом решения линейных уравнений является метод Бернулли. Пусть дано уравнение (1). Решение этого уравнения будем искать в виде произведения двух функций:  , где  ,  . Подставим решение в исходное уравнение (3.6):

                                        ,

                                     ,

                                     .

Найдем такую функцию  , которая бы являлась решением дифференциального уравнения

                                               .

Тогда решение уравнения (1) будет сведено к решению системы уравнений с разделяющимися переменными

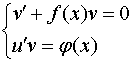                                                                                                 (7)

Заметим, что при решении первого уравнения системы достаточно указать любое частное решение, то есть выбор константы произволен.

Пример. Решить дифференциальное уравнение.

                                                 .

Решение. Данное уравнение является линейным. Решим его двумя способами.

1 способ. Решим уравнение методом вариации произвольной постоянной. Соответствующее однородное уравнение имеет вид:

                                                  .

Это уравнение с разделяющимися переменными:

                                                   ,

                                       ,  ,

                                ,  ,

                                                      .

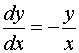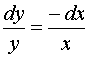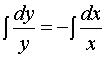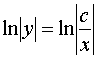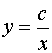Найдено общее решение однородного уравнения. Общее решение неоднородного уравнения ищем в том же виде, полагая  :

                                   ;  .

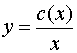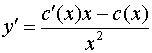Подстановка в первоначальное уравнение приводит к равенству

                                      .

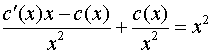Решим полученное дифференциальное уравнение относительно неизвестной функции  :

                                              ,  ,

                                           ,  ,

                                    ,  .

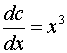Подставив в выражение   найденную функцию   получим общее решение линейного уравнения:

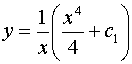                                или  ,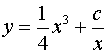

где   - произвольная постоянная. Решение представляет собой сумму вида (3.11), где  ,  .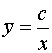

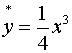2 способ. Решим это же уравнение методом Бернулли, полагая, что  , где  ,  . Исходное уравнение примет вид:

                                           ,

                                          .

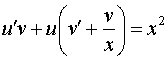Система (7) может быть записана как

                                                 

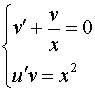
Решение первого уравнения системы:

                                ,  ,  ,

                                ;  .

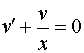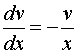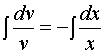Частное решение уравнения (при  ):  . Подставив функцию   во второе уравнение системы, получим:

                                 ,  ,  ,

                                                  .

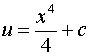Общее решение линейного уравнения:

                                          ,

                                                .

 

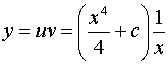Метод Лагранжа.

Задача состоит в вычислении какого–либо частного решения линейного неоднородного дифференциального уравнения с непрерывными коэффициентами и непрерывной правой частью.

Рассмотрим линейное неоднородное дифференциальное уравнение

y⁽ⁿ⁾ + a_n-1(x)y^{(n - 1)} + ... + a₁(x)y' + a₀(x)y = f(x).

с нерерывными на [a; b] коэффициентами и непрерывной правой частью.

Предположим, что известна фундаментальная система y₁(x), y₂(x),..., y_n(x) решений соответствующего однородного уравнения   y⁽ⁿ⁾ + a_n-1(x)y^{(n - 1)} + ... + a₁(x)y' + a₀(x)y = 0.

Будем искать частное решение неоднородного уравнения в виде

y*(x) = C₁(x) y₁(x) + C₂(x) y₂(x) + ... + C_n(x) y_n(x) ,

где C₁(x), C₂(x) , ... , C_n(x) — неизвестные, n раз дифференцируемые на [a; b] функции. Их называют варьируемые постоянные общего решения однородного уравнения.

Справедливо следующее утверждение.

Пусть y₁(x), y₂(x),..., y_n(x) — фундаментальная система решений однородного уравнения   y⁽ⁿ⁾ + a_n-1(x)y^{(n - 1)} + ... + a₁(x)y' + a₀(x)y = 0 с непрерывными на отрезке [a; b] коэффициентами. Если правая часть f(x) неоднородного уравнения   y⁽ⁿ⁾ + a_n-1(x)y^{(n - 1)} + ... + a₁(x)y' + a₀(x)y = f(x) непрерывна на [a; b], то его частное решение можно искать в виде

y*(x) = y(x,C₁,..., C_n) = C₁(x) y₁(x) + C₂(x) y₂(x) + ... + C_n(x) y_n(x) .

Неизвестные функции C₁(x), C₂(x) , ... , C_n(x) находятся из системы

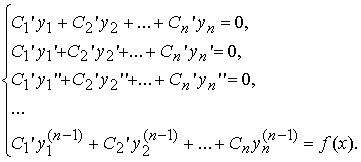
Такой метод отыскания частного решения неоднородного уравнения называется методом вариации произвольных постоянных или методом Лагранжа.

Пример:

Найдём методом Лагранжа (методом вариации произвольных постоянных) частное решение линейного неоднородного дифференциального уравнения второго порядка

с непрерывными на (e, ∞) коэффициентами и непрерывной правой частью.

Фундаментальную систему решений соответствующего однородного уравнения образуют функции y₁(x) = ln x , y₂(x) = x.

Будем искать частное решение неоднородного уравнения в виде y*(x) = C₁(x) lnx + C₂(x) x:

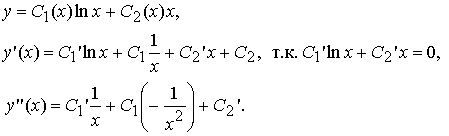
Подставим выражения для производных в уравнение:

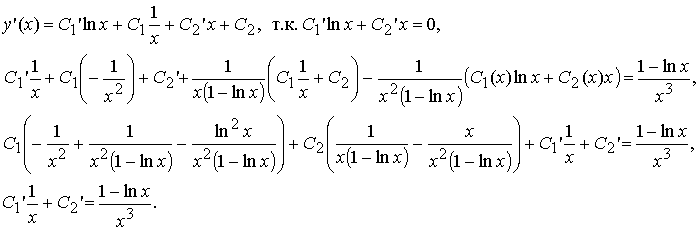
Для неизвестных функций C₁(x), C₂(x) получили систему линейных дифференциальных уравнений второго порядка:

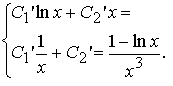
Окуда имеем:

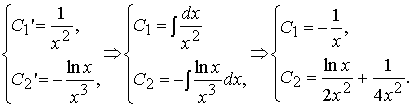
И тогда частным решением исходного уравнения второго порядка является функция y*(x) = C₁(x) lnx + C₂(x) x:

Билет 5

Метод Бернулли

  Пределы Интеграл Типовые задачи С помощью дифференциала функции вычислить приближённо    при x = 7,76. Справочный материал и примеры к выполнению контрольной работы по математике

  Суть метода заключается в том, что искомая функция представляется в виде произведения двух функций  .

  При этом очевидно, что   - дифференцирование по частям.

 

  Подставляя в исходное уравнение, получаем:

 Далее следует важное замечание – т.к. первоначальная функция была представлена нами в виде произведения, то каждый из сомножителей, входящих в это произведение, может быть произвольным, выбранным по нашему усмотрению.

  Например, функция   может быть представлена как 

 и т.п.

  Таким образом, можно одну из составляющих произведение функций выбрать так, что выражение  .

  Таким образом, возможно получить функцию u, проинтегрировав, полученное соотношение как однородное дифференциальное уравнение по описанной выше схеме:

 

 

  Для нахождения второй неизвестной функции v подставим поученное выражение для функции u в исходное уравнение   с учетом того, что выражение, стоящее в скобках, равно нулю.

 

  Интегрируя, можем найти функцию v:

;  ;

  Т.е. была получена вторая составляющая произведения  , которое и определяет искомую функцию.

  Подставляя полученные значения, получаем:

 

 

 Окончательно получаем формулу:

, С₂ - произвольный коэффициент.

Это соотношение может считаться решением неоднородного линейного дифференциального уравнения в общем виде по способу Бернулли.

Билет 6.

Уравнение бернулли.

Обыкновенное дифференциальное уравнение вида:

называется уравнением Бернулли (при n = 0 или n = 1 получаем неоднородное или однородное линейное уравнение). При n = 2 является частным случаем уравнения Риккати. Названо в честь Якоба Бернулли, опубликовавшего это уравнение в 1695 году. Метод решения с помощью замены, сводящей это уравнение к линейному, нашёл его брат Иоганн Бернулли в 1697 году.^[1]